Изучение собственных колебаний струны

ЦЕЛЬ РАБОТЫ:

· Изучение колебаний в системах с распределёнными параметрами на примере поперечных стоячих волн в упругой горизонтальной струне.

· Наблюдение картины распределения амплитуд колебаний точек струны при образовании стоячих волн.

· Количественная проверка формулы скорости распространения колебаний вдоль струны.

КРАТКАЯ ТЕОРИЯ:

СТОЯЧИЕ ВОЛНЫ – это особый случай интерференции, возникающий при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами:

x₁ =Acos (wt – kx), x₂ = A cos (wt + kx) (1)

Сложив эти уравнения и учитывая, что k = 2p/l, получим уравнение стоячей волны:

x =x₁ +x₂ = 2А cos kx cos wt = 2A cos (2px/l) cos wt. (2)

Из уравнения (2) следует, что в каждой точке этой волны происходят колебания с одной и той же частотой w и амплитудой 2A cos (2px/l), зависящей от координаты х рассматриваемой точки.

В точках среды, где 2px/l =± mp (m = 0,1,2,…), амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где 2px/l = ±(m +1/2)p, амплитуда колебаний обращается в нуль.

Точки, в которых амплитуда максимальна, называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.

В гибкой однородной струне, натянутой между двумя точками и выведенной из положения равновесия, могут установиться стоячие волны. При этом на длине струны L всегда должно укладываться целое число стоячих волн. При этом струна делится неподвижными точками – узлами – на несколько равных отрезков, длина которых равна половине длины бегущей волны. Следовательно, можно записать

L = n (l/2), (3)

где n – целое число, определяющее количество полуволн, уложившихся на всей длине струны L.

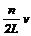Так, как длина волны l связана со скоростью распространения волны v и частотой n соотношением v = ln, то, учитывая (3), имеем n= . (4)

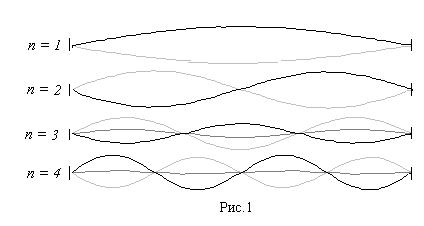
Струна, следовательно, может колебаться не с одной частотой, а с целым спектром частот, соответствующим собственным (нормальным) колебаниям струны. В общем случае любые сложные колебания в струне можно представить как суперпозиция нескольких собственных колебаний, отличающихся не только своими частотами, но и своими амплитудами для отдельных точек струны. Распределение амплитуд отдельных точек волны при собственных колебаниях для различных значений n имеет вид, изображённый на рис.1.

Опыт показывает, что скорость распространения импульса деформаций (колебаний) вдоль струны определяется силой натяжения струны F и линейной плотностью m материала струны:

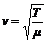. (5)

Тогда с учётом формулы (5) формула (4) примет вид:

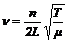. (6)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

1. Установите с помощью движков регуляторов постоянные значения линейной плотности материала и силы натяжения струны, указанных в таблице 1 для вашей бригады.

2. Установите начальную частоту колебания струны f = 1,0 Гц и, постепенно увеличивая её значение, получите устойчивые колебания струны при n = 1 (см распределение амплитуд точек струны при n = 1).

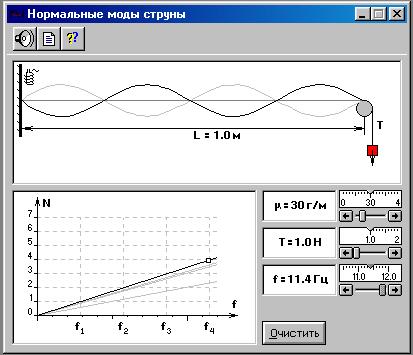
3. Аналогичным образом получите стоячие волны соответствующие различным значениям n и заполните табл.2.

4. Установите второе значение линейной плотности материала струны из табл.1 для вашей бригады и проделайте измерения п.2 и 3 ещё раз и заполните табл.3.

Таблица 1.

№ бригады
Т, Н	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8
m, г/м	5,1 9,1	5,2 9,2	5,3 9,3	5,4 9,4	5,5 9,5	5,6 9,6	5,7 9,7	5,8 9,8	5,1 9,1	5,2 9,2	5,3 9,3	5,4 9,4	5,5 9,5	5,6 9,6	5,7 9,7	5,8 9,8