Исследование решений уравнения параболического типа

Еще один пример использования конечных разностей – уравнение теплопроводности (диффузии).

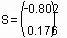
Это уравнение параболического типа. Явная разностная схема для этого уравнения имеет вид

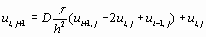(2.1)

Эта разностная схема устойчива, если 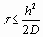. Для краткости в дальнейшем мы будем обозначать весь множитель, стоящий перед скобкой, как k.

Задаем коэффициент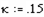
и диапазон изменения пространственной и временной координат:

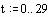
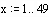
Задаем начальные и граничные условия

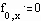
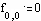
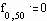
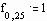
Уравнение в конечных разностях имеет вид

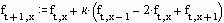
Представляем результаты на графике. (Для большей наглядности изображена только центральная часть)

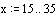
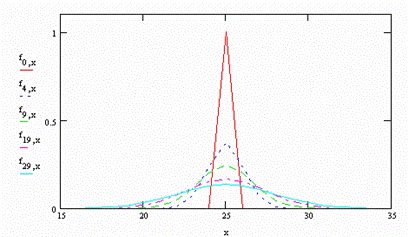
Рис. 2.1.

Основное достоинство явных методов – их простота – зачастую сводится на нет достаточно жесткими ограничениями на величину шага. Явные схемы обычно устойчивы при столь малых шагах по времени, что они становятся непригодными для практических расчетов. Этого существенного недостатка позволяют избежать неявные схемы. Свое название они получили потому, что значения искомой функции на очередном временном шаге не могут быть явно выражены через значения функции на предыдущем шаге.

Рассмотрим применение неявной схемы на примере уравнения теплопроводности

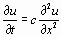(2.2)

Запишем неявную разностную схему для этого уравнения

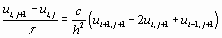(2.3)

Здесь первый индекс соответствует пространственной, а второй – временной координате. В отличие от явной схемы, для вычисления в правой части уравнения используются значения функции на том же самом временном шаге. Вводя обозначение 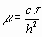, уравнение (2.3) можно переписать в виде

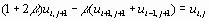(2.4)

или в матричной форме

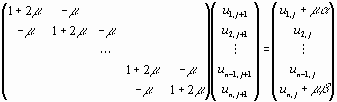(2.5)

где .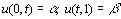

Задаем количество узлов сетки (в данном случае оно одинаково для обеих переменных)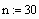

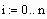
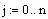
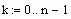
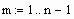
Задаем значения параметров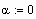

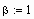
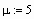
и начальное распределение температуры в области

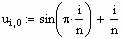
Формируем матрицы уравнения (2.5)

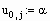
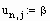
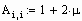
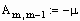
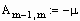
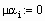
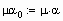
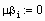
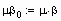
Находим решение системы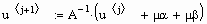

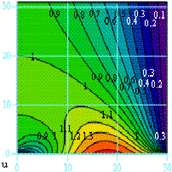
Рис. 2.2.

Начиная с версии Mathcad 11 для решения уравнений в частных производных можно использовать встроенную функцию pdesolve. Эта функция применяется в рамках вычислительного блока, начинающегося ключевым словом Given, и пригодна для решения различных гиперболических и параболических уравнений.

Встроенная функция для решения одномерного уравнения (или системы уравнений) в частных производных, зависящего от времени t и пространственной координаты х, работает следующим образом.

· Pdesolve(u, x, xrange, t, trange, [xpts] , [tpts]) — возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x, t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме.

o u — явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр.

o х —пространственная координата (имя аргумента неизвестной функции).

o xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала).

o t — время (имя аргумента неизвестной функции).

o trange — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени).

o xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически).

o tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).

Помимо этой функции для решения параболических и гиперболических уравнений, начиная с версии Mathcad 11, можно использовать еще одну встроенную функцию numol (). Функция numol () имеет еще большее число аргументов и позволяет управлять дополнительными параметрами метода сеток.

В качестве примера использования этой функции Mathcad используем то же самое одномерное уравнение теплопроводности (2.2) с граничными условиями U(0,t) = 0, U(L, t) = 0 и начальным условием 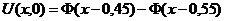, где Ф(х) = 1.

Пример 2.1. Решение одномерного уравнения теплопроводности

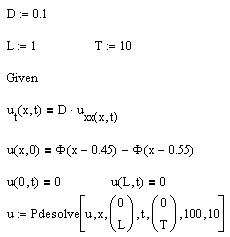
Для корректного использования функции Pdesolve предварительно, после ключевого слова Given, следует записать само уравнение и граничные условия при помощи логических операторов. Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x, t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции Pdesolve). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например, u_xx(x ,t) для обозначения второй производной функции и по пространственной координате х.

Как видно из рис. 2.3, на котором изображены результаты расчетов, встроенная функция с успехом справляется с уравнением диффузии, отыскивая уже хорошо знакомое нам решение. Заметим, что использование встроенной функции Pdesolve связано с довольно громоздкими вычислениями, которые могут отнимать существенное время.

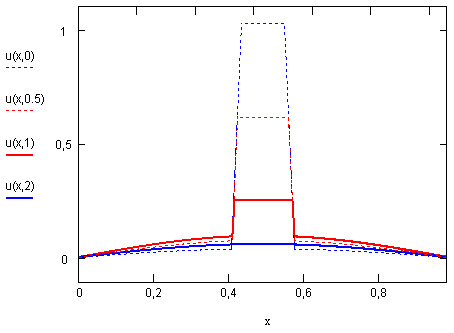
Рис. 2.3. Решение уравнения диффузии тепла при помощи встроенной функции Pdesolve

Для визуализации распространения тепла (процесса диффузии) с течением времени можно использовать такую возможность, как создание анимационного клипа. Принцип анимации в Mathcad – кадровая анимация. Расчет производится в цикле отдельно для каждого кадра. Одним из аргументов формул и графиков должен являться номер кадра, который задается системной переменной FRAME, принимающей только натуральные значения.

Для функции u(x, t)

Для задания времени используем следующую запись

Т1:= FRAME.

Далее, после перехода к рисунку и выделения участка документа, на котором приведена зависимость u(x, t), необходимо вызвать диалоговое окно Record Animation в меню Tool. В нем задается начальное From и конечное To значения переменной FRAME, и скорость отображения At (кадр/с). Выделенный участок отображается штрихованной линией, образующей прямоугольную область. Затем нажимаем кнопку Animate, а по окончании вычислений записываем полученный клип в файл.

Задания:

1. Решить уравнение параболического типа (теплопроводности, диффузии) с помощью разностной схемы и встроенной Mathcad-функции pdesolve при заданных начальных и граничных условиях. Построить график зависимости U = U(x, t₁) в моменты времени t₁ = 0, 10, 20 секунд.

2.Сделать запись анимированного клипа, показывающего изменение функции U = U(x, T), полученной в Зад. 1, со временем при T:= FRAME.

Начальные и граничные условия:

№	Задание 1
Гранич. усл	Нач. усл.
19.	U(0,t) = 0, U(p, t) = 0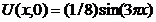
20.	U(0,t) = 0, U(p, t) = 0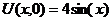
21.	U(0,t) = 0, U(p, t) = 0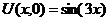
22.	U(0,t) = 0, U(p, t) = 0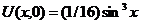
23.	Uх(0,t) = 0, Uх(1, t) = 0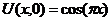
24.	Uх(0,t) = 0, Uх(1, t) = 0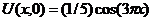
25.	Uх(0,t) = 0, Uх(1, t) = 0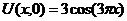
26.	Uх(0,t) = 0, Uх(1, t) = 0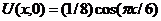
27.	U(0,t) = 0, Uх(1, t) = 0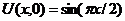
28.	Uх(0,t) = 0, U(1, t) = 0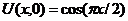
29.	U(0,t) = 0, Uх(1, t) = 0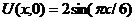
30.	Uх(0,t) = 0, U(1, t) = 0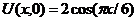
31.	U(0,t) = 0, Uх(1, t) = 0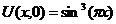

Лабораторная работа №3