Исследование решений уравнения гиперболического типа

Лабораторная работа №1

Исследование решений уравнения гиперболического типа

Одним из методов решения дифференциальных уравнений в частных производных является метод сеток. Идея метода заключается в следующем. Для простоты, ограничимся случаем только функции двух переменных, и будем полагать, что решение уравнения ищется на квадратной области единичного размера. Разобьем область сеткой. Шаг сетки по оси x и по оси y, вообще говоря, может быть разный. По определению частная производная равна

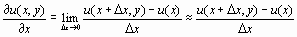
Если рассматривать функцию только в узлах сетки, то частную производную можно записать в форме

,

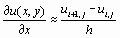где узел 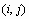соответствует точке 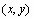. Полученное выражение называется правой конечной разностью. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.

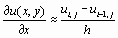
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.

Теперь получим выражения для вторых производных.

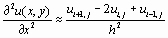
В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.

В качестве примера рассмотрим решение волнового уравнения (уравнения гиперболического типа).

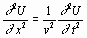
Уравнение будем решать методом сеток. Запишем уравнение в конечных разностях

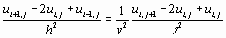
Полученное уравнение позволяет выразить значение функции u в момент времени 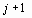через значения функции в предыдущие моменты времени.

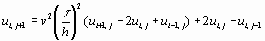
Такая разностная схема называется явной, так как искомая величина получается в явном виде. Она устойчива, если .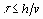

Пример 1.1. Зададим начальные условия: смещение струны U в начальный и последующий моменты времени описывается синусоидальной функцией.

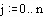
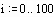
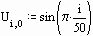
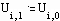
(Совпадение смещений при j=0 и j=1 соответствует нулевой начальной скорости.)

Зададим граничные условия: на концах струны смещение равно 0 в любой момент времени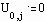

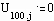
Будем полагать коэффициент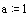

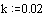
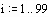
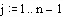
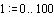
Записываем уравнение в конечных разностях, разрешенное относительно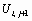

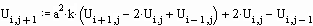
Представляем результат на графике

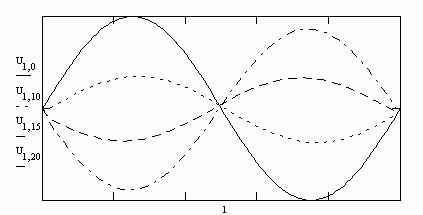
Рис. 1.1.

В случае, если имеется аналитическое решение гиперболического уравнения с заданными начальными и граничными условиями, то представить графически поведение функции U = U(x, T) в любой момент времени Т можно с помощью элемента управления Slider (ползунковый регулятор). Данный элемент устанавливает шаблон, позволяющий изменять значения указанной переменной от T = 0 до T = T_max с шагом 1. Величина T_max должна являться целым числом.

Пример 1.2.

Вставим элемент Slider в рабочее поле (рис 1.2).

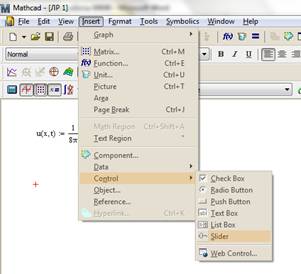
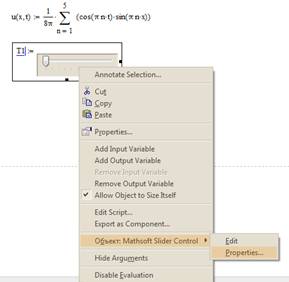
Рис. 1.2. Рис. 1.3.

Вставим имя переменной и вызовем свойства объекта (рис. 1.3).

Зададим начальное T = 0 и конечное T = T_max значения времени и построим график u(x, T1) зависимости для заданного положением регулятора времени T1.

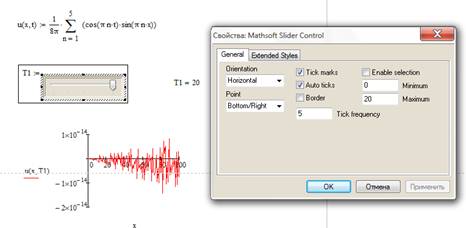
Рис. 1.4.

Задания:

1. Для заданного аналитического решения уравнения гиперболического типа
а) построить график зависимости U = U(x, t₁) в моменты времени t₁ = 0, 10, 20 секунд;

б) построить (если это возможно) с использованием объекта slider графики зависимости U = U(x, T), T := slider и U = U(x,0), n := slider.

2. Решить уравнение гиперболического типа методом конечных разностей при следующих начальных и граничных условиях.

№	Задание 1 U = U(x,t)	Задание 2
Гранич. Усл	Начальные условия
1.		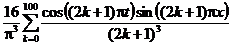U(0,t) = 0, U(l, t) = 0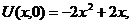
2.		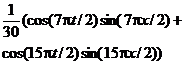U(0,t) = 0, U(l, t) = 0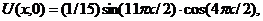
3.		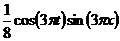U(0,t) = 0, U(l, t) = 0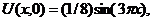
4.		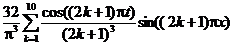U(0,t) = 0, U(l, t) = 0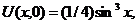
5.		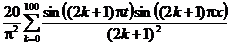U(0,t) = 0, U(l, t) = 0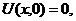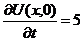
6.		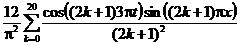U(0,t) = 0, U(l, t) = 0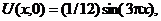
7.		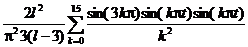U(0,t) = 0, U(l, t) = 0	,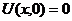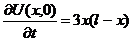
8.		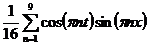U(0,t) = 0, U(l, t) = 0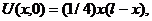
9.		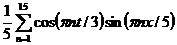U(0,t) = 0, U(l, t) = 0	,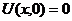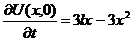
10.		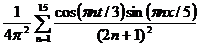U(0,t) = 0, U(l, t) = 0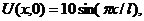
11.		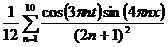U(0,t) = 0, U(l, t) = 0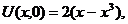
12.		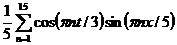U(0,t) = 0, U(l, t) = 0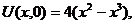
13.		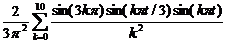U(0,t) = 0, U(l, t) = 0	,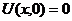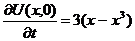
14.		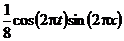U(0,t) = 0, U(l, t) = 0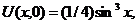
15.		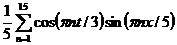U(0,t) = 0, U(l, t) = 0	,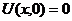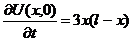
16.		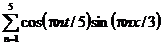U(0,t) = 0, U(l, t) = 0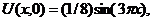
17.		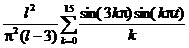U(0,t) = 0, U(l, t) = 0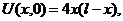
18.		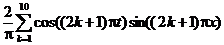U(0,t) = 0, U(l, t) = 0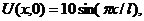

Лабораторная работа №2

Лабораторная работа №3

Лабораторная работа №4

Лабораторная работа №5

Лабораторная работа №1

Исследование решений уравнения гиперболического типа

Одним из методов решения дифференциальных уравнений в частных производных является метод сеток. Идея метода заключается в следующем. Для простоты, ограничимся случаем только функции двух переменных, и будем полагать, что решение уравнения ищется на квадратной области единичного размера. Разобьем область сеткой. Шаг сетки по оси x и по оси y, вообще говоря, может быть разный. По определению частная производная равна

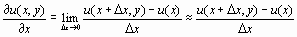
Если рассматривать функцию только в узлах сетки, то частную производную можно записать в форме

,

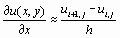где узел 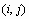соответствует точке 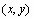. Полученное выражение называется правой конечной разностью. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.

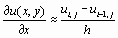
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.

Теперь получим выражения для вторых производных.

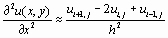
В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.

В качестве примера рассмотрим решение волнового уравнения (уравнения гиперболического типа).

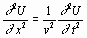
Уравнение будем решать методом сеток. Запишем уравнение в конечных разностях

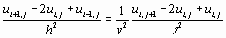
Полученное уравнение позволяет выразить значение функции u в момент времени 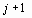через значения функции в предыдущие моменты времени.

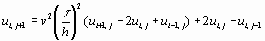
Такая разностная схема называется явной, так как искомая величина получается в явном виде. Она устойчива, если .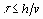

Пример 1.1. Зададим начальные условия: смещение струны U в начальный и последующий моменты времени описывается синусоидальной функцией.

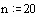
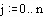
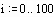
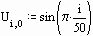
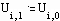
(Совпадение смещений при j=0 и j=1 соответствует нулевой начальной скорости.)

Зададим граничные условия: на концах струны смещение равно 0 в любой момент времени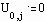

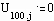
Будем полагать коэффициент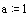

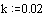
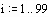
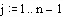
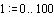
Записываем уравнение в конечных разностях, разрешенное относительно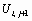

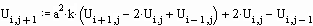
Представляем результат на графике

Рис. 1.1.

В случае, если имеется аналитическое решение гиперболического уравнения с заданными начальными и граничными условиями, то представить графически поведение функции U = U(x, T) в любой момент времени Т можно с помощью элемента управления Slider (ползунковый регулятор). Данный элемент устанавливает шаблон, позволяющий изменять значения указанной переменной от T = 0 до T = T_max с шагом 1. Величина T_max должна являться целым числом.

Пример 1.2.

Вставим элемент Slider в рабочее поле (рис 1.2).

Рис. 1.2. Рис. 1.3.

Вставим имя переменной и вызовем свойства объекта (рис. 1.3).

Зададим начальное T = 0 и конечное T = T_max значения времени и построим график u(x, T1) зависимости для заданного положением регулятора времени T1.

Рис. 1.4.

Задания:

1. Для заданного аналитического решения уравнения гиперболического типа
а) построить график зависимости U = U(x, t₁) в моменты времени t₁ = 0, 10, 20 секунд;

б) построить (если это возможно) с использованием объекта slider графики зависимости U = U(x, T), T := slider и U = U(x,0), n := slider.

2. Решить уравнение гиперболического типа методом конечных разностей при следующих начальных и граничных условиях.

№	Задание 1 U = U(x,t)	Задание 2
Гранич. Усл	Начальные условия
1.		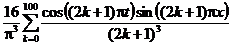U(0,t) = 0, U(l, t) = 0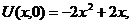
2.		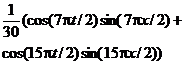U(0,t) = 0, U(l, t) = 0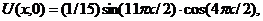
3.		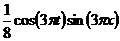U(0,t) = 0, U(l, t) = 0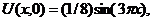
4.		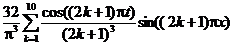U(0,t) = 0, U(l, t) = 0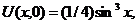
5.		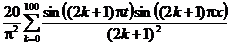U(0,t) = 0, U(l, t) = 0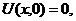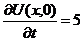
6.		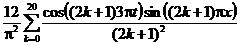U(0,t) = 0, U(l, t) = 0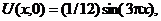
7.		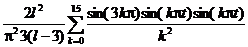U(0,t) = 0, U(l, t) = 0	,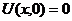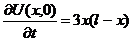
8.		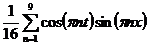U(0,t) = 0, U(l, t) = 0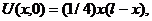
9.		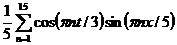U(0,t) = 0, U(l, t) = 0	,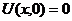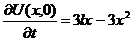
10.		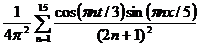U(0,t) = 0, U(l, t) = 0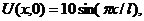
11.		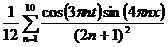U(0,t) = 0, U(l, t) = 0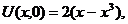
12.		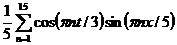U(0,t) = 0, U(l, t) = 0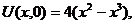
13.		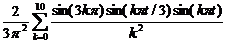U(0,t) = 0, U(l, t) = 0	,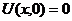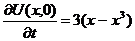
14.		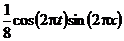U(0,t) = 0, U(l, t) = 0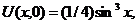
15.		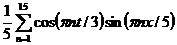U(0,t) = 0, U(l, t) = 0	,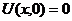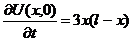
16.		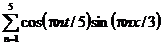U(0,t) = 0, U(l, t) = 0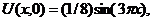
17.		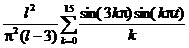U(0,t) = 0, U(l, t) = 0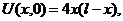
18.		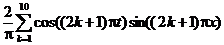U(0,t) = 0, U(l, t) = 0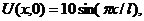

Лабораторная работа №2