Корреляционно-регрессионный анализ

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

Виды зависимостей

Признаки, которыми обладают элементы совокупности, существуют неизолированно, они взаимосвязаны между собой. Так, производительность труда на предприятиях зависит от уровня механизации и электрификации производства, стажа и квалификации рабочих и ряда других признаков (факторов). Например, урожайность зерновых зависит от количества внесенных удобрений, срока посева, различных погодно-климатических факторов.

Зависимость между признаками будет функциональной, если каждому значению одного признака соответствует вполне определенное значение другого признака. Подобная зависимость в основном встречается в естественных науках. В экономических же науках между признаками существует статистическая зависимость, при которой каждому значению одного признака соответствует целый ряд распределения другого признака. Так, при одной и той же электровооруженности производительность труда рабочих на различных предприятиях одной отрасли будет разной. Это можно объяснить тем, что производительность труда зависит не только от электровооруженности, но и от ряда других факторов, которые в данный момент не учитываются.

Зависимую переменную принято называть результативным признаком (фактором) и обозначать У. Признаки (факторы), влияющие на результативный признак У, называют факторными признаками и обозначают Х₁, Х₂, ..., Х_n.

Статистическая зависимость между двумя признаками Х и У называется парной. Она задается следующей таблицей:

xi	х1	х2	...	хn
yi	y1	y2	...	yn	,

если данные наблюдений не сгруппированы, или корреляционной таблицей:

У \ Х	х1	х2	...		...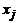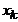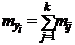
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
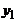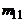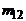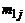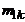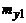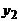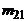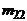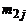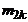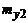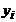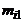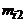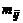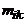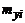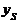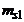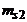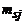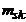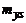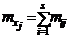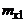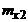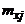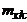			...		...		n	,

если данные сгруппированы,

.

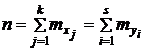Частота 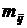показывает, сколько раз встречается пара 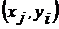во всех наблюдениях.

В корреляционной таблице наглядно видны ряды распределения одного признака, соответствующие каждому значению другого признака, которые называются условными распределениями. Так, значению х₁ признака Х соответствует следующий ряд распределения признака У:

y1	y2	...	yi	...	ys
		...		...		,

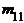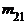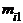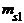значению х_j:

y1	y2	...	yi	...	ys
		...		...		.

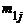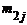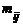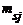Аналогично для признака У значению у_i соответствует следующий ряд распределения признака Х:

х1	х2	...	хj	...	хk
		...		...		.

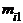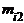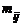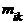По каждому условному ряду распределения можно найти среднюю величину, называемую условной средней и вычисляемую по формуле 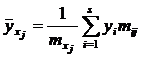. В результате получим соответствие между значениями одного признака и условнымисредними другого признака, то есть:

xj	х1	х2	...	хk
			...		.

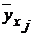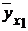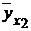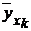Если каждому значению одного признака соответствует вполне определенная условная средняя другого признака, то есть между значениями одного признака и условными средними другого признака наблюдается функциональная связь, то зависимость между этими признаками будем называть корреляционной.

Если с увеличением признака Х условная средняя признака У растет, то корреляционная зависимость называется положительной (прямой). Корреляционная зависимость будет отрицательной (обратной), если с ростом признака Х условная средняя признака У убывает. Если же условная средняя не изменяется, то корреляционная зависимость между признаками отсутствует.

Пример 1.Данные о себестоимости единицы продукции (р.) и производительности труда (тыс. шт.) 50 предприятий представлены в виде следующей корреляционной таблицы:

Себестоимость единицы продукции	Производительность труда
					Итого
Итого

Определить, существует ли между этими признаками корреляционная зависимость.

Решение. Пусть признак У - себестоимость единицы продукции, р.; Х - месячная производительность труда, тыс. шт. В этой таблице наглядно представлены условные распределения каждой случайной величины. Так, для х₁ = 11 условное распределение признака У имеет следующий вид:

yi
			,

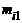для у₄=13:

хj
					.

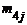Найдем условные средние признака У для каждого значения признака Х.

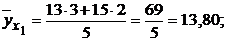
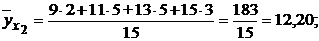
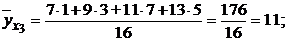
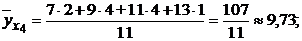
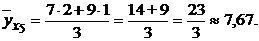
Результаты вычислений представим в виде таблицы:

хj
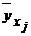	13,8	12,2		9,73	7,67	.

Итак, себестоимость единицы продукции (У) и производительность труда (Х) связаны между собой корреляционной зависимостью.

Определение формы парной

Корреляционной зависимости

С помощью корреляционного анализа изучается теснота взаимосвязи между признаками. Регрессионный анализ позволяет приближенно представить корреляционную зависимость между признаками в виде некоторого уравнения, называемого уравнением регрессии.

Пусть Х и У - признаки, связанные между собой корреляционной зависимостью, которая может быть линейной, гиперболической, параболической или какой-то другой. Поэтому необходимо предварительно выяснить форму корреляционной зависимости. Данные задачи можно решить графически. Для этого строятся точки с координатами (х_i, 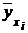), если данные сгруппированы в корреляционную таблицу, или (х_i, у_i), если данные не сгруппированы. По расположению построенных точек подбирается линия (прямая, гипербола, парабола), уравнение которой известно (рис. 1, 2, 3).

Рис. 1

Рис. 2

Рис. 3

Так, расположение точек на рис. 1 позволяет сделать вывод, что зависимость между признаками линейная, уравнение прямой у=а₀+а₁х принимается за уравнение регрессии. По рис. 2, 3 делаем вывод, что за уравнение регрессии следует принимать, соответственно, уравнение гиперболы 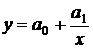и уравнение параболы у=а₀+а₁х+а₂х².

Далее необходимо найти неизвестные числа а₀, а₁, а₂, называемые параметрами уравнений регрессии. Их определяют, например, методом наименьших квадратов, сущность которого заключается в следующем: находятся такие параметры уравнения регрессии, чтобы была минимальной сумма квадратов отклонений эмпирических значений признака У от теоретических, вычисленных по уравнению регрессии, то есть .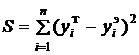

Регрессионный анализ

Корреляционный анализ

ТАБЛИЦА НАБЛЮДЕНИЙ

------------------------------------------------------------------------

N X1(У) X2(Х) X3(Х²)

------------------------------------------------------------------------

1 1.74 55 3025

2 2.02 65 4225

3 2.12 75 5625

4 2.05 85 7225

5 2.17 95 9025

6 2.74 105 11025

7 2.40 115 13225

8 2.48 125 15625

9 2.50 135 18225

10 2.39 145 21025

------------------------------------------------------------------------

----РЕЗУЛЬТАТЫ РАСЧЕТА МНОГОМЕРНОЙ РЕГРЕССИИ---------------

Y=A0+A1*Х1+А2*Х2+А3*Х3+...+Ap*Xp

-------------------------------------------------------------------------------------------------------

*НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ*

N СРЕД. СР.КВ.ОТКЛ. КОР-ИЯ К-Т РЕГ. СР.Р. Т

3 10825.00 6103.55 0.7378 -0.0001 0.0001 -2.04

2 100.00 30.28 0.7909 0.0362 0.0141 2.56

*ЗАВИСИМАЯ ПЕРЕМЕННАЯ*

N СРЕД. СР.КВ.ОТКЛ.

1 2.26 0.29 a₁ a₂

------------------------------------------------------------------------------------------------------

СВОБОДНЫЙ ЧЛЕН А0 = 0.185 а₀

------------------------------------------------------------------------------------------------------

*ТАБЛИЦА ОСТАТКОВ ВЫЧИСЛЕНИЯ ЗАВИСИМОЙ ПЕРЕМЕННОЙ*

N ЗАДАННОЕ ЗНАЧ. ВЫЧИСЛЕННОЕ ЗНАЧ. ОСТАТОК

1 1.74 1.75 -0.01

2 2.02 1.94 0.08

3 2.12 2.10 0.02

4 2.05 2.23 -0.18

5 2.17 2.34 -0.17

6 2.74 2.41 0.33

7 2.40 2.46 -0.06

8 2.48 2.48 0.00

9 2.50 2.47 0.03

10 2.39 2.43 -0.04

-------------------------------------------------------------------------------------------------

Вычисленные на ПК параметры уравнения регрессии a₀ , a₁ , a₂ дают уравнение регрессии следующего вида:

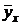» 0,185 + 0,0362x - 0,0001x².

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

Виды зависимостей

Признаки, которыми обладают элементы совокупности, существуют неизолированно, они взаимосвязаны между собой. Так, производительность труда на предприятиях зависит от уровня механизации и электрификации производства, стажа и квалификации рабочих и ряда других признаков (факторов). Например, урожайность зерновых зависит от количества внесенных удобрений, срока посева, различных погодно-климатических факторов.

Зависимость между признаками будет функциональной, если каждому значению одного признака соответствует вполне определенное значение другого признака. Подобная зависимость в основном встречается в естественных науках. В экономических же науках между признаками существует статистическая зависимость, при которой каждому значению одного признака соответствует целый ряд распределения другого признака. Так, при одной и той же электровооруженности производительность труда рабочих на различных предприятиях одной отрасли будет разной. Это можно объяснить тем, что производительность труда зависит не только от электровооруженности, но и от ряда других факторов, которые в данный момент не учитываются.

Зависимую переменную принято называть результативным признаком (фактором) и обозначать У. Признаки (факторы), влияющие на результативный признак У, называют факторными признаками и обозначают Х₁, Х₂, ..., Х_n.

Статистическая зависимость между двумя признаками Х и У называется парной. Она задается следующей таблицей:

xi	х1	х2	...	хn
yi	y1	y2	...	yn	,

если данные наблюдений не сгруппированы, или корреляционной таблицей:

У \ Х	х1	х2	...		...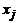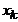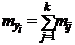
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
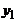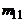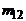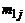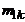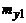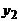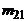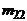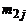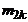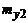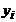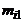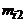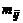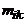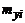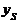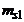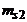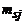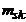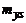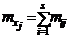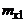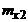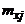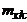			...		...		n	,

если данные сгруппированы,

.

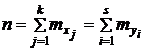Частота 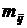показывает, сколько раз встречается пара 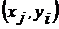во всех наблюдениях.

В корреляционной таблице наглядно видны ряды распределения одного признака, соответствующие каждому значению другого признака, которые называются условными распределениями. Так, значению х₁ признака Х соответствует следующий ряд распределения признака У:

y1	y2	...	yi	...	ys
		...		...		,

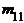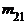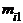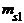значению х_j:

y1	y2	...	yi	...	ys
		...		...		.

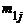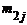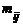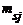Аналогично для признака У значению у_i соответствует следующий ряд распределения признака Х:

х1	х2	...	хj	...	хk
		...		...		.

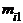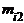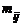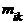По каждому условному ряду распределения можно найти среднюю величину, называемую условной средней и вычисляемую по формуле 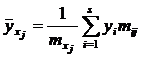. В результате получим соответствие между значениями одного признака и условнымисредними другого признака, то есть:

xj	х1	х2	...	хk
			...		.

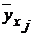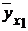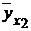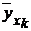Если каждому значению одного признака соответствует вполне определенная условная средняя другого признака, то есть между значениями одного признака и условными средними другого признака наблюдается функциональная связь, то зависимость между этими признаками будем называть корреляционной.

Если с увеличением признака Х условная средняя признака У растет, то корреляционная зависимость называется положительной (прямой). Корреляционная зависимость будет отрицательной (обратной), если с ростом признака Х условная средняя признака У убывает. Если же условная средняя не изменяется, то корреляционная зависимость между признаками отсутствует.

Пример 1.Данные о себестоимости единицы продукции (р.) и производительности труда (тыс. шт.) 50 предприятий представлены в виде следующей корреляционной таблицы:

Себестоимость единицы продукции	Производительность труда
					Итого
Итого

Определить, существует ли между этими признаками корреляционная зависимость.

Решение. Пусть признак У - себестоимость единицы продукции, р.; Х - месячная производительность труда, тыс. шт. В этой таблице наглядно представлены условные распределения каждой случайной величины. Так, для х₁ = 11 условное распределение признака У имеет следующий вид:

yi
			,

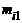для у₄=13:

хj
					.

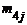Найдем условные средние признака У для каждого значения признака Х.

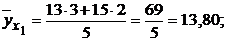
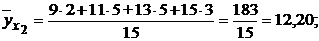
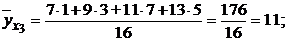
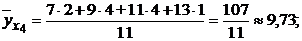
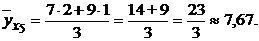
Результаты вычислений представим в виде таблицы:

хj
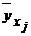	13,8	12,2		9,73	7,67	.

Итак, себестоимость единицы продукции (У) и производительность труда (Х) связаны между собой корреляционной зависимостью.

Определение формы парной

Корреляционной зависимости

С помощью корреляционного анализа изучается теснота взаимосвязи между признаками. Регрессионный анализ позволяет приближенно представить корреляционную зависимость между признаками в виде некоторого уравнения, называемого уравнением регрессии.

Пусть Х и У - признаки, связанные между собой корреляционной зависимостью, которая может быть линейной, гиперболической, параболической или какой-то другой. Поэтому необходимо предварительно выяснить форму корреляционной зависимости. Данные задачи можно решить графически. Для этого строятся точки с координатами (х_i, 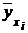), если данные сгруппированы в корреляционную таблицу, или (х_i, у_i), если данные не сгруппированы. По расположению построенных точек подбирается линия (прямая, гипербола, парабола), уравнение которой известно (рис. 1, 2, 3).

Рис. 1

Рис. 2

Рис. 3

Так, расположение точек на рис. 1 позволяет сделать вывод, что зависимость между признаками линейная, уравнение прямой у=а₀+а₁х принимается за уравнение регрессии. По рис. 2, 3 делаем вывод, что за уравнение регрессии следует принимать, соответственно, уравнение гиперболы 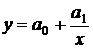и уравнение параболы у=а₀+а₁х+а₂х².

Далее необходимо найти неизвестные числа а₀, а₁, а₂, называемые параметрами уравнений регрессии. Их определяют, например, методом наименьших квадратов, сущность которого заключается в следующем: находятся такие параметры уравнения регрессии, чтобы была минимальной сумма квадратов отклонений эмпирических значений признака У от теоретических, вычисленных по уравнению регрессии, то есть .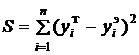

Регрессионный анализ