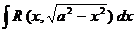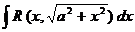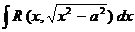Интегрирование тригонометрических выражений.
Пусть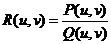 
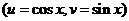, где 
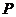и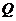 
- многочлены от 
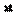и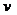 
.
1) Если один из многочленов 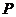, 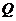четный по 
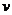, а другой – нечетный по 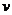, то подстановка 
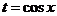рационализирует интеграл.
2) Если один из многочленов 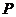, 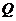четный по 
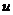, а другой – нечетный по 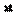, то подстановка 
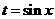рационализирует интеграл.
3) Если оба многочлена четные по 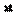и 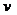, то подстановка 
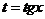рационализирует интеграл.
3’) Выражения вида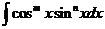 
, где 
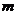и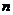 
- четные. Они сходны с 3 случаем, где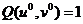 
4) Универсальная подстановка.
Рационализация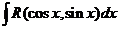 
также достигается с помощью подстановки 
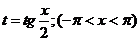, которая называется универсальной. В самом деле,
; 
; 
.
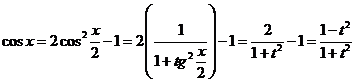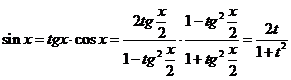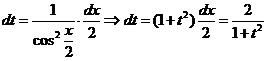
5) Выражения вида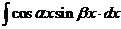 
; 
; 
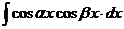. Они рационализируются с помощью перевода в тригонометрические суммы.
Билет 36
Тригонометрические подстановки.
Следующие интегралы превращаются в тригонометрические выражения при помощи тригонометрических подстановок:
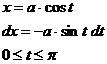
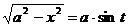
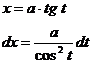
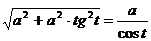
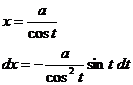
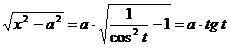
Пример:
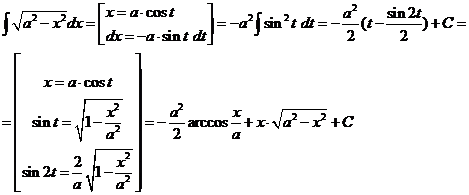
Билет 37
Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
Пусть задана функция f(x) на отрезке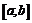 
. Составим разбиение R: 
.
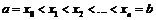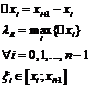
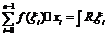
Это интегральная сумма, соответствующая разбиению R и выбору точек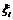 
.
Если существует предел при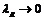 
интегральных сумм 
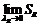, и он не зависит от R и 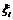, то он называется определенным интегралом Римана.
Определение по Коши:
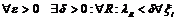
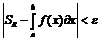
По Гейне:
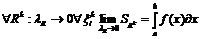, где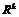 
- последовательность разбиений.
Критерий Коши:
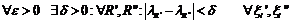
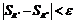
Билет 38
Ограниченность интегрируемой функции.
Теорема:
Если функция f(x) интегрируема на [a,b] и существует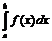 
, то функция ограничена на этом отрезке.
Доказательство:
От противного: пусть f(x) неограниченна на [a,b]. Введем произвольное разбиение R: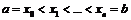 
. Т.к. функция неограниченна на [a,b], то она неограниченна хотя бы на одном из отрезков 
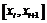. Пусть 
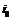- номер того отрезка, на котором функция неограниченна. Тогда рассмотрим интегральную сумму:
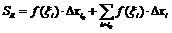- т.е. выделили суммы одно слагаемое. Обозначим 
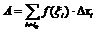, тогда получим:
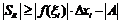(следует из неравенства о модулях). Тогда возьмем произвольное N и сделаем разность 
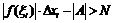. Для этого у нас должно быть 
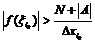. У нас функция неограниченна на отрезке 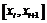, значит 
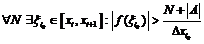. Тогда интегральная сумма будет 
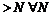, т.е. будет являться величиной неограниченной, т.е. не будет существовать ее предела, а значит и 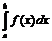, что противоречит условию.
Теорема доказана.
Билет 39
Суммы Дарбу. Их Свойства.
Определение:
Пусть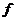 
ограничена на отрезке 
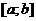. Введём разбиение R этого отрезка.
R: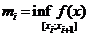 
, 
.
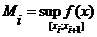Тогда можем составить выражения:
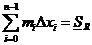- нижняя сумма Дарбу, 
- верхняя сумма Дарбу.
, 
.
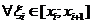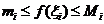Пусть 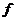ограничена на отрезке 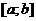. Введём разбиение R этого отрезка.
R: , .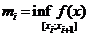
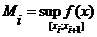Тогда можем составить выражения:
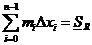- нижняя сумма Дарбу, - верхняя сумма Дарбу.
, .
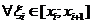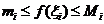Свойства сумм Дарбу:
1) 
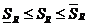, для одного и того же разбиения.
2) Рассмотрим два разбиения в случае, когда одно разбиение является продолжением другого. Т.е.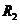 
- продолжение 
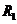, если все точки 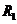являются точками .
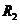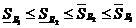
Добавление точек не увеличивает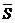 
и не уменьшает 
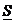. Пусть 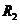получается из 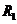добавлением одной точки.
, 
,
,
,
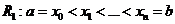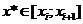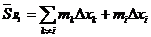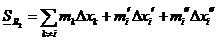Заметим, что если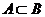 
, то 
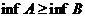и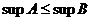 
. Отсюда заключаем:
, 
, 
, 
.
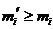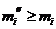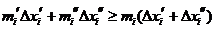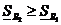3) 
, 
,
,
=> 
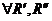
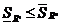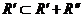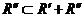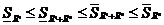, т.е.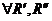 
.
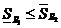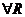
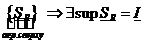- нижний интеграл (нижняя точная сумма Дарбу).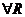 
.
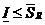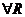
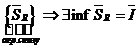- верхний интеграл (верхняя точная сумма Дарбу).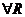 
.
.
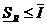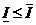Билет 40