Дифференциал, производные высших порядков

Пример 1. Найти дифференциалы функций

1. ; 2. ,

вычислить .

Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:

1. ;

2.

.

Свойства дифференцируемых функций

Пример 1. Найти пределы, используя правило Лопиталя.

1. ; 2. ; 3. ; 4. .

Решение. Убедившись, что имеет место неопределенность или , применяем затем правило Лопиталя.

1.

;

2.

;

здесь правило Лопиталя применено дважды.

3.

;

4. .

Исследование поведения функций

Пример 1. Исследовать и построить график функции

.

Решение.

1. Заданная функция определена и непрерывна на всей числовой оси

.

2. Функция нечетная, ибо , ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для .

3. График функции пересекается с осями координат только в начале координат, так как .

4. Исследуем функцию на наличие асимптот:

а) вертикальных асимптот график функции не имеет;

б) невертикальная асимптота имеет уравнение .

,

.

Таким образом, уравнение асимптоты .

5. Исследуем функцию на экстремум

.

нигде не обращается в нуль; не существует в точках , которые являются критическими.

Исследуем знак производной на интервале [0; ∞) (рис.5)

0 1

Рис. 5.

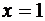есть точка максимума, .

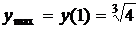6. Исследуем график функции на выпуклость и вогнутость

.

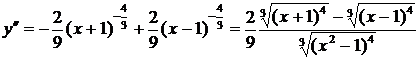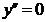в точке 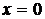; 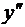не существует в точках 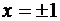. Эти точки могут быть абциссами точек перегиба.

Исследуем знак второй производной на интервале [0; ∞) (рис.6)

0 1

Рис. 6

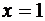не является точкой перегиба.

Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0) (рис.7)

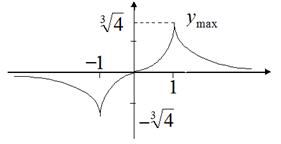
Рис. 7

Пример 2. Найти наибольшее и наименьшее значения функции

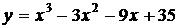на отрезке [-4; 4].

Решение. 1. Найдем критические точки функции 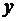, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках: 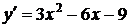; 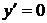в точках 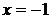и 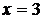. Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках: 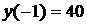и .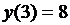

2. Вычислим значения функции на концах отрезка [-4; 4]: 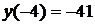и .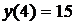

3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции 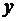на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке 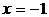, а ее наименьшее значение равно -41 и достигается на левой границе отрезка .

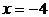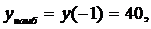
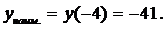
Функции нескольких переменных

Литература. [1], гл.VШ, § 1 - 4.

1. Частные производные.

Литература. [1], гл. VIII, § 5, 6, упр. 1-10.

Пример.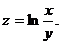

1. Найти область определения функции.

2. Проверить, что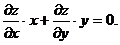

3. Проверить, что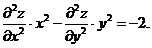

Решение.

1. Под знаком логарифма может стоять только положительное выражение, следовательно

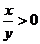
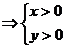или .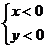

Сделаем чертеж

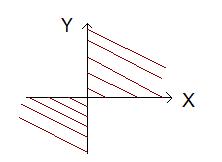
Рис. 3.

2. При вычислении частной производной по 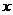рассматриваем функцию 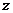как функцию только от переменной 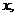а при дифференцировании по 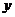- как функцию только от :

,

,

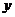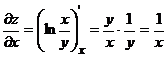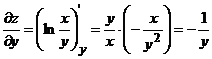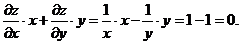
3. При вычислении второй производной по 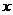также рассматриваем функцию 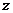как функцию только от переменной 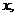а при дифференцировании по 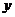- как функцию только от :

,

,

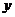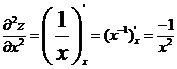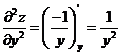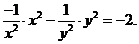
Контрольная работа 2. Задания

1. Найти точки разрыва функции, если они существуют. Сделать чертеж функции.

1.1.	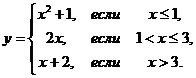1.11.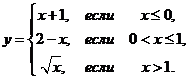
1.2.	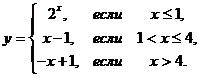1.12.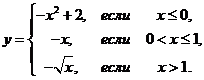
1.3.	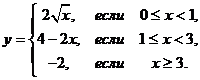1.13.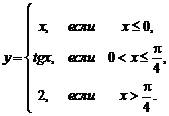
1.4.	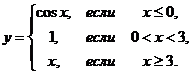1.14.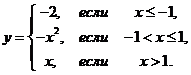
1.5.	1.15.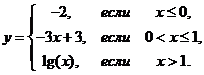
1.6.	1.16.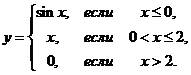
1.7.	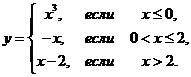1.17.
1.8.	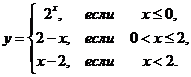1.18.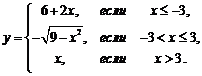
1.9.	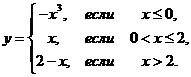1.19.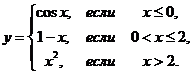
1.10.	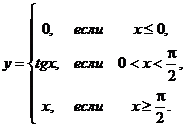1.20.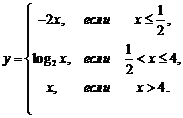

2. Найти производные 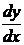данных функций.

№	а	б	в	г
2.1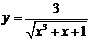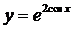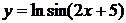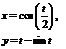
2.2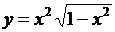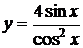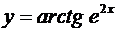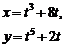
2.3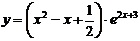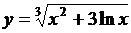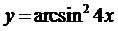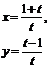
2.4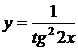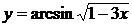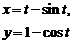
2.5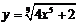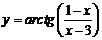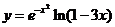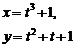
2.6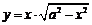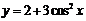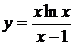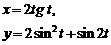
2.7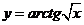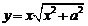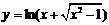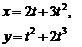
2.8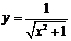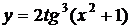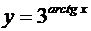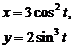
2.9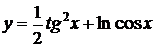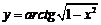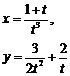
2.10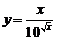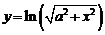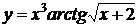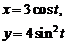
2.11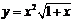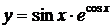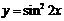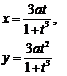
2.12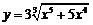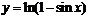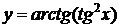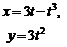
2.13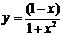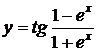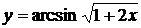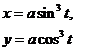
2.14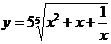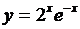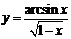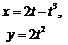
2.15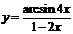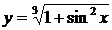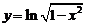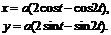
2.16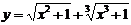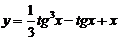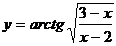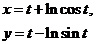
2.17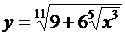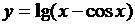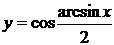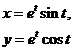
2.18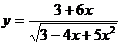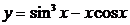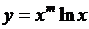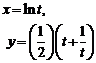
2.19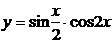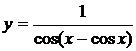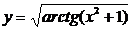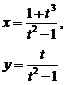
2.20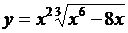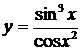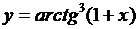

3.Найти указанные пределы, использую правило Лопиталя.

	а	б
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12.
3.13
3.14
3.15
3.16
3.17
3.18
3.19
1.20.

4. Найти интервалы монотонности и экстремумы функции.

4.1. ;	4.11. ;
4.2. ;	4.12. ;
4.3. ;	4.13. ;
4.4. ;	4.14. ;
4.5. ;	4.15. ;
4.6. ;	4.16. ;
4.7. ;	4.17. ;
4.8. ;	4.18. ;
4.9. ;	4.19. ;
4.10. ;	4.20. ;

5. Дана функция двух переменных

Проверить, удовлетворяет ли функция двух переменных указанному дифференциальному уравнению первого порядка.

5.1
5.2	,
5.3	,
5.4	,
5.5	,
5.6	,
5.7
5.8	,
5.9	,
5.10.	,
5.11	,
5.12	,
5.13	,
5.14	,
5.15	,
5.16	,
5.17	,
5.18	,
5.19	,
5.20	,

Библиографический список

1. Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры. –М.: Наука, 2005.

2. Письменный Д. Конспект лекций по высшей математике, Айрис Пресс, т.1, 2, 2011 г.

3. Пискунов Н.С.Дифференциальное и интегральное исчисления. Т. 1, 2. - М.: Наука, 2009.

4. Минорский В.П. , Сборник задач по высшей математике, 2009 г.

5. Данко П.Е., Попов А.Г. и др., Высшая математика в упражнениях и задачах,

т.т. 1-2, 2007 г.

Вопросы к зачету

№ п/п	Формулировка вопроса
	Матрицы и определители
	Системы линейных уравнений. Формулы Крамера
	Векторы в геометрической и координатной форме (свойства и действия)
	Произведения векторов
	Прямая на плоскости, различные виды её уравнения
	Угол между прямыми, условия их параллельности и перпендикулярности
	Кривые второго порядка(окружность, эллипс, гипербола, парабола), их канонические уравнения, свойства, чертёж
	Плоскость в пространстве, различные виды её уравнения
	Прямая в пространстве, различные виды её задания
	Предел функции. Теоремы о пределах. Раскрытие неопределённостей
	Производная, её определение, геометрический и механический смысл, правила вычисления
	Дифференциал функции, его геометрический смысл
	Производные и дифференциалы высших порядков
	Теоремы Ролля и Лагранжа, их геометрический смысл
	Правило Лопиталя для раскрытия неопределённостей
	Применение понятия производной для исследования свойств функции: - возрастание и убывание, - точки экстремума, - выпуклость и вогнутость её графика, - точки перегиба графика, - асимптоты (вертикальные и наклонные)
	Функции двух переменных (определение, область определения, способы задания, частные производные)