Решение системы трех линейных уравнений методами Крамера и Гаусса.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
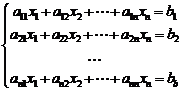 | 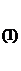 |
Вычислим определитель системы 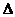
 | 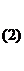 |
Как известно, если 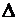 ¹0, то система (1) имеет решение, и при том единственное. Если
¹0, то система (1) имеет решение, и при том единственное. Если 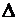 =0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
=0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
В дальнейшем мы будем предполагать, что 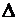 ¹0.
¹0.
1. Решение с помощью формул Крамера.
Если определитель системы 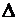 ¹0, то, согласно формулам Крамера, решение системы (1) можно представить в виде
¹0, то, согласно формулам Крамера, решение системы (1) можно представить в виде
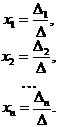 | 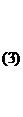 |
Здесь
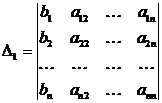 ; ; | 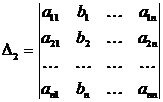 ; ; | ||
 . . | 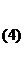 | ||
Определитель 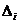 (i=1, 2,…, n) отличается от определителя системы
(i=1, 2,…, n) отличается от определителя системы 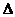 тем, что
тем, что 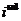 столбец
столбец 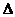 заменен столбцом из свободных членов, т.е. столбец
заменен столбцом из свободных членов, т.е. столбец 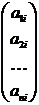 заменен на столбец
заменен на столбец  .
.
Пример. Дана расширенная матрица системы 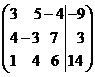 . Решить систему методом Крамера.
. Решить систему методом Крамера.
Решение. Запишем систему в стандартной форме
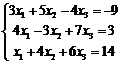 .
.
Определитель данной системы
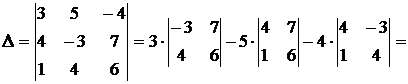
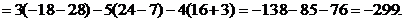
Вычислим определители 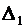 ,
, 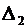 и
и 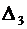 :
:
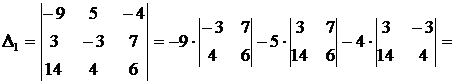
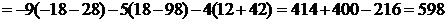 .
.
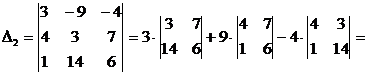
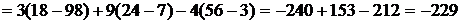 .
.
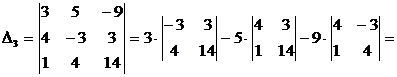
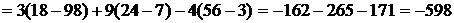 .
.
Решение системы: 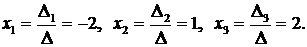
Для того чтобы убедиться в правильности решения, подставим эти значения 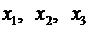 в исходную систему
в исходную систему
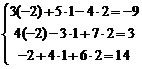 .
.
2. Решение методом Гаусса. Пусть есть система (1) с определителем 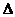 ¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
 . . | 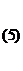 |
Метод Гаусса состоит в том, что система (1) с помощью ряда элементарных преобразований сводится к новой системе, расширенная матрица которой имеет вид
 . . |  |
Т.е. в результате преобразований все коэффициенты матрицы 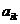 становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:
становятся равными нулю, кроме диагональных элементов, которые становятся равными единице: 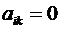 при
при 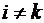 и
и 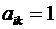 при
при 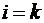 . Столбец свободных членов
. Столбец свободных членов  превращается в новый столбец
превращается в новый столбец  .
.
Если мы привели нашу матрицу к диагональному виду, то решение системы записывается очень просто:
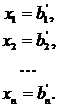 |
Таким образом, решение системы сводится к совершению элементарных преобразований, в результате которых расширенная матрица (5) превращается в расширенную матрицу (6).
К элементарным преобразованиям системы (1) относятся следующие:
1) перемена местами уравнений (т.е. перемена местами строк расширенной матрицы);
2) умножение или деление любого уравнения системы (1) на число, отличное от 0 (т.е. умножение или деление строки расширенной матрицы на число, отличное от 0);
3) изменение любого уравнения системы (1) путем прибавления к нему другого уравнения системы, умноженного на число, отличное от 0 (т.е. изменение строки расширенной матрицы путем прибавления к ней другой строки, умноженной на число, отличное от 0).
Пример. Найти решение системы методом Гаусса.
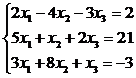 .
.
Решение.Определитель системы 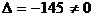 . Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
. Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
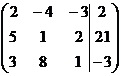 .
.
Далее мы будем приводить нашу матрицу к диагональному виду и выписывать ее вид после каждого шага преобразований.
1-й шаг. Разделим 1-ю строку матрицы на 2.
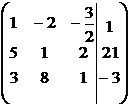 .
.
2-й шаг. 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:
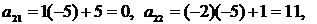
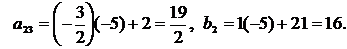
Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда
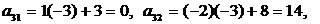
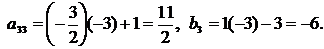
Расширенная матрица примет вид
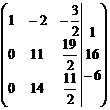 .
.
В результате первых 2-х шагов 1-й столбец  преобразовался в
преобразовался в  .
.
3-й шаг. Делим вторую строку на 11.
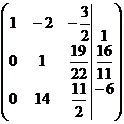 .
.
4-й шаг. 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда
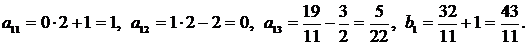
Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на (-14) и складываем ее с 3-й строкой, тогда
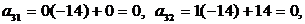
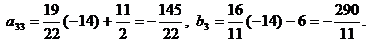
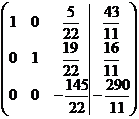 .
.
В результате 3-го и 4-го шагов 1-й столбец матрицы не изменился, а 2-й превратился в 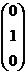 .
.
5-й шаг. Делим 3-ю строку на 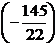
 .
.
6-й шаг. 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 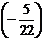 и складываем ее с 1-й строкой, тогда
и складываем ее с 1-й строкой, тогда
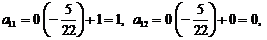
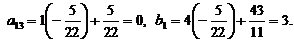
Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 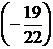 и складываем ее со 2-й строкой, тогда
и складываем ее со 2-й строкой, тогда
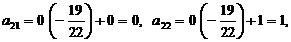
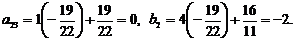
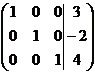 .
.
В результате 5-го и 6-го шагов 3-й столбец принял вид 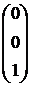 .
.
Таким образом, решение системы следующее: 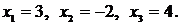 Проверка
Проверка
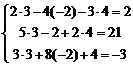
Таким образом, смысл метода Гаусса состоит в том, что сначала 1-й столбец исходной матрицы приводим к виду  , затем 2-й - к виду
, затем 2-й - к виду  и, наконец, 3-й – к виду
и, наконец, 3-й – к виду  . При этом происходит преобразование столбца свободных членов.
. При этом происходит преобразование столбца свободных членов.
Решение методом исключений.Метод исключений является модификацией метода Гаусса и удобен для небольших систем.
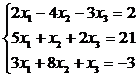 .
.
Умножим первое уравнение на коэффициент при х1 из второго уравнения, т.е. на 5, а второе на коэффициент при х1 из второго уравнения, т.е. на 2 и вычтем друг из друга. Потом умножим первое на коэффициент при х1 из второго уравнения, т.е. на 3, а третье на 5 и снова вычтем
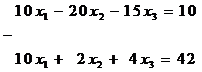
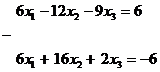
_______________________________ ___________________
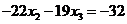
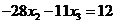
Поменяем в первом уравнении знаки и запишем подсистему
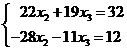
Умножим первое уравнение на 28, второе на 22 и сложим. Слагаемые с х2 сократятся и мы получим уравнение для х3
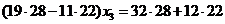
х3 = 4, подставляя х3 в первое уравнение подсистемы получим х2
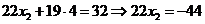 , х2 = -2,
, х2 = -2,
Подставляя х2 и х3 в первое уравнение системы найдем х1
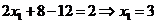
Объем вычислений при этом методе существенно меньше.
Системы координат
Пример. Найти расстояние между точками М1(1, -2, -3) и М2(-3, 1, 1). Определить координаты точки С, делящей отрезок М1М2 в отношении 2:3.
Решение.
Используя формулу
М1М2 = 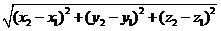
 ,
,
получим М1М2 = 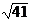 .
.
2. Координаты точки С определим по формуле вида
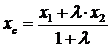 ,
,
где 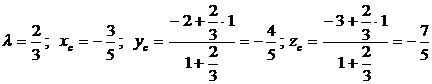 .
.
Векторная алгебра
Пример 1. Даны точки М1(1, -2, -3), М2(-3, 1, 1). Найти длину вектора 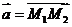 .
.
Решение.Вектор 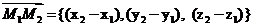 . Следовательно
. Следовательно 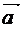 = {-3-1, 1+2, 1+3} ={-4, 3, 4}. Длина вектора находится по формуле ça ç=
= {-3-1, 1+2, 1+3} ={-4, 3, 4}. Длина вектора находится по формуле ça ç= 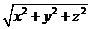 .
. 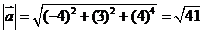
Пример 2.Найти угол φ между векторами 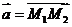 и
и 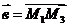 , если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
, если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
Решение. Для нахождения cosφ используем формулу
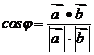
где 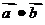 - скалярное произведение векторов
- скалярное произведение векторов 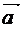 и
и 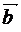 .
.
Определим координаты векторов 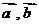 и cosφ:
и cosφ:
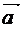 = (-3-1, 1+2, 1+3) =(-4, 3, 4),
= (-3-1, 1+2, 1+3) =(-4, 3, 4), 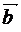 = (3-1, 2+2, 2+3) = (2, 4, 5),
= (3-1, 2+2, 2+3) = (2, 4, 5),
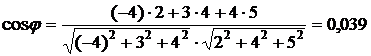 ,
,
φ = 87045'54".
Пример 3. Даны координаты вершин пирамиды А1(1, -2, -3), А2(-3, 1, 1), А3(4, 3, -1), А4(3, 2, 2). Найти площадь грани А1 А2 А3 и объем пирамиды.
Решение. Площадь треугольника А1А2А3 найдем, используя геометрический смысл векторного произведения векторов
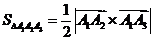 ,
,
где 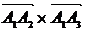 - векторное произведение векторов.
- векторное произведение векторов.
Вначале находим 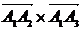
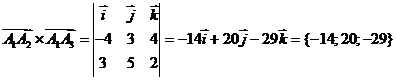 ,
,
а затем
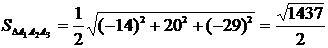 ед2.
ед2.
Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
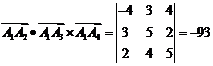 ,
,
следовательно, 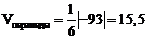 ед3.
ед3.
