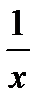Вычисление определённого интеграла
Рассмотрим на примере нахождения первообразной. Пусть в интеграле  аргумент изменяется от x=2 до x=4. Найдём приращение первообразной функции
аргумент изменяется от x=2 до x=4. Найдём приращение первообразной функции 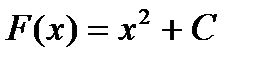
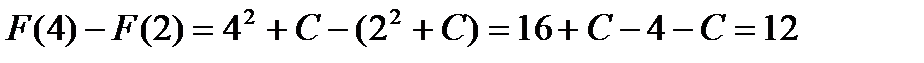
Приращение первообразной функции от постоянной не зависит; его и назвали определённым интегралом.
Обозначается символом: 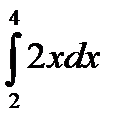 .
.
Вычисления записывают: 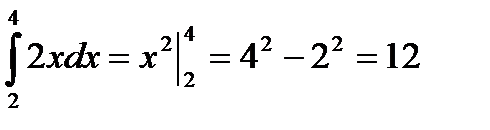
Определение. Приращение первообразной 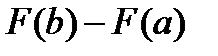 при изменении аргумента от x=a до x=b называется определённым интегралом
при изменении аргумента от x=a до x=b называется определённым интегралом 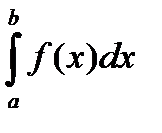 ,
,
где a – нижний предел интегрирования,
b - верхний предел интегрирования.
Правило. Чтобы вычислить определённый интеграл, нужно найти соответствующий неопределённый интеграл, в полученное выражение подставить вместо x сначала верхний, затем нижний пределы интегрирования, а результат найти вычитанием.
Для вычисления определённого интеграла используется формула Ньютона-Лейбница: 
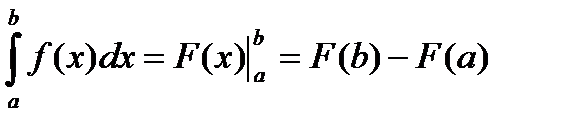
Свойства определённого интеграла:
1)постоянный сомножитель можно выносить за знак интеграла (k=const)
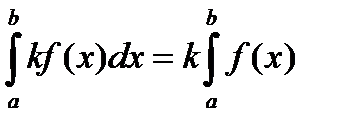
2)определённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждой функции
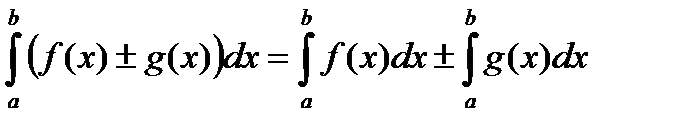
3)если переставить пределы интегрирования, то знак определённого интеграла измениться на противоположный
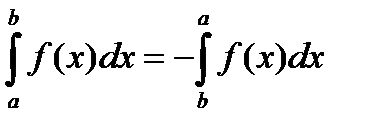 .
.
Пример 1. Вычислить 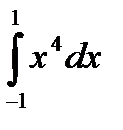 .
.
Решение. Согласно формуле Ньютона-Лейбница имеем: 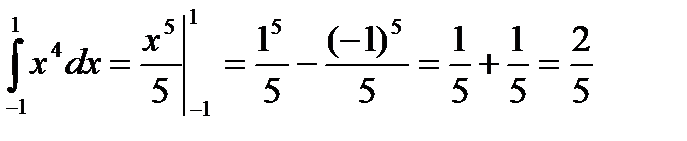 .
.
Пример 2. Вычислить 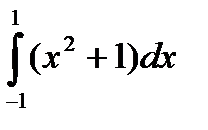 .
.
Решение. 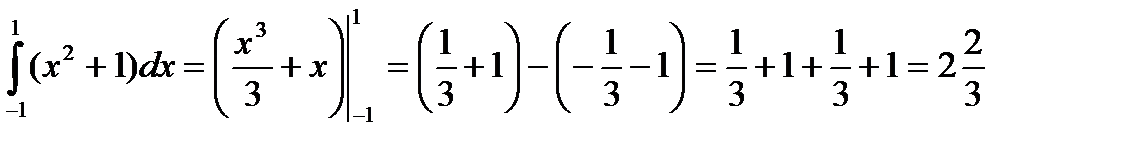 .
.
Пример 3. Вычислить 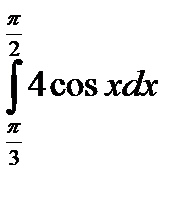 .
.
Решение. 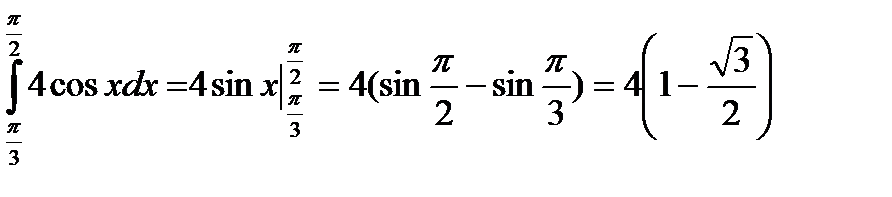 .
.
Примечание. Значения тригонометрических функций смотри в приложении.
Пример 4. Вычислить 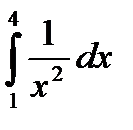 .
.
Решение: 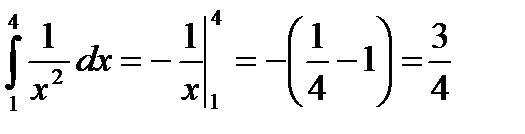 .
.
Пример 5. Вычислить 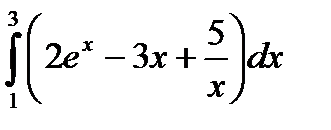
Решение: 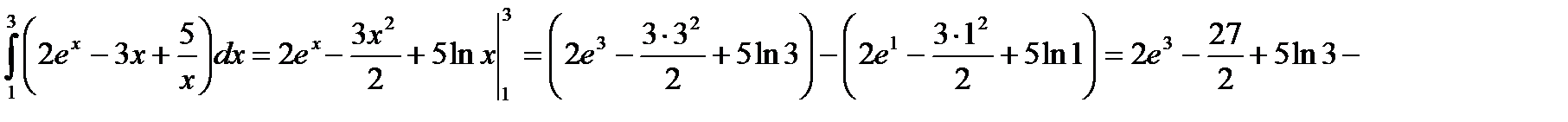

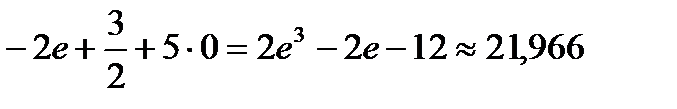
Вычисление площадей фигур
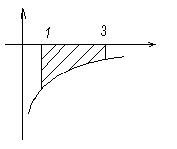
Определение.Криволинейной трапецией (рис. 1) называют фигуру, которая ограничена:
| · сверху - графиком непрерывной функции y=y(x) · снизу – осью OX (y=0) · слева – прямой x=a · справа – прямой x=b |
Утверждение.Геометрический смысл определённого интеграла в том, что его значение равно площади соответствующей криволинейной трапеции:
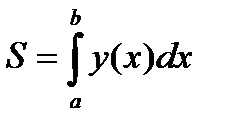 (1)
(1)
Рассмотрим различные методы вычисления площадей плоских фигур.
Пример 1.Вычислить площадь плоской фигуры, ограниченной линиями: 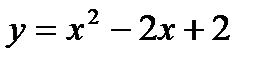 , x=-1, x=2 и осью OX.
, x=-1, x=2 и осью OX.
Решение: данная фигура (рис. 2) представляет собой криволинейную трапецию, поэтому её площадь вычисляется по формуле (1).
| 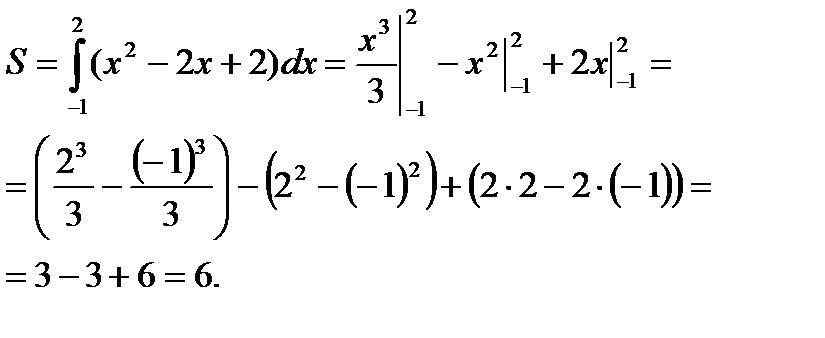 Ответ: 6 кв.ед. Ответ: 6 кв.ед. |
Пусть y=f(x) – непрерывная функция при x 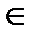 [a, b], график которой расположен ниже оси OX (рис. 3). Значение определённого интеграла будет отрицательным, поэтому для расчёта площади берём значение интеграла по модулю.
[a, b], график которой расположен ниже оси OX (рис. 3). Значение определённого интеграла будет отрицательным, поэтому для расчёта площади берём значение интеграла по модулю.
| 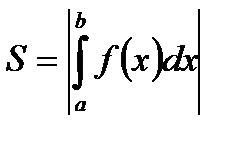 (2) (2) |
Пример 2. Вычислить площадь плоской фигуры, ограниченной графиком функции 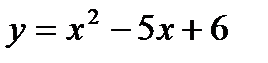 и осью OX.
и осью OX.
Решение: данная фигура (рис. 4) расположена ниже оси OX, поэтому применим формулу (2).
| 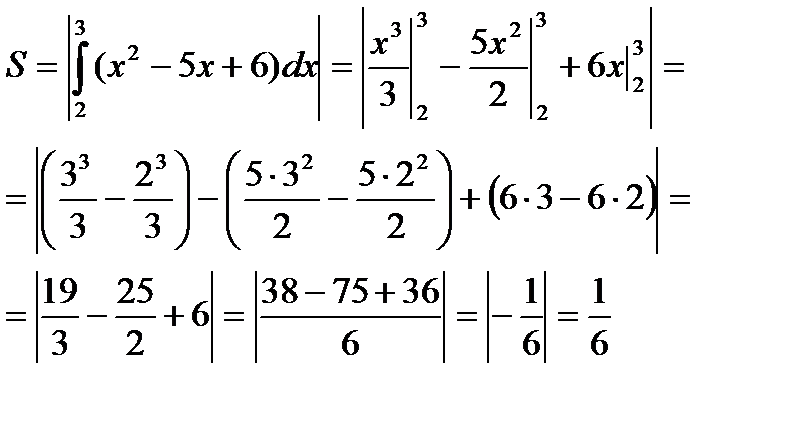 Ответ: 1/6 кв.ед. Ответ: 1/6 кв.ед. |
Пример 3. Вычислить площадь плоской фигуры, ограниченной графиками функций 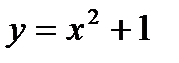 и
и 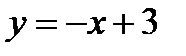 .
.
Решение: данная фигура (рис. 5)представляет собой разность криволинейных трапеций
Абсциссы точек пересечения находим по чертежу: x1=-2 и x2=1.
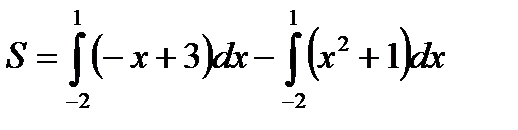 . Можно записать под один интеграл:
. Можно записать под один интеграл:
|
| 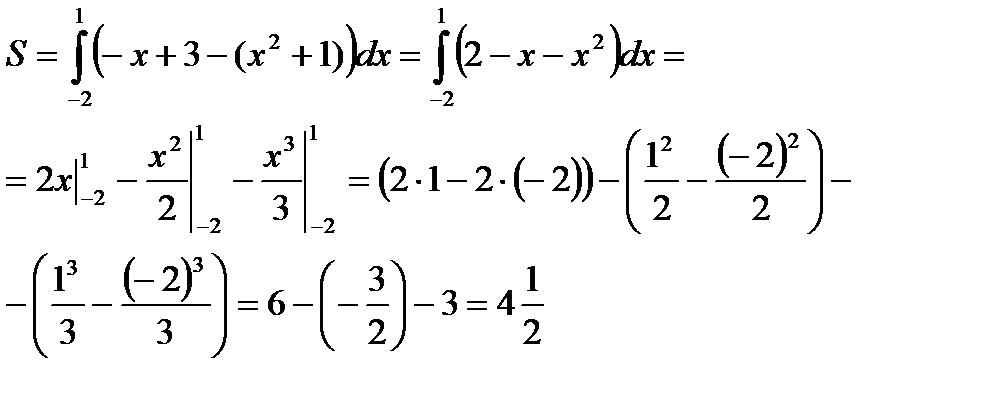 Ответ: 4,5 кв.ед. Ответ: 4,5 кв.ед. |
Пример 4.Вычислить площадь плоской фигуры, ограниченной графиками функций 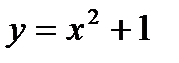 и
и 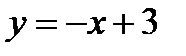 , и координатными осями.
, и координатными осями.
Решение: данная фигура (рис. 6) представляет собой сумму криволинейных трапеций S=S1+S2, где 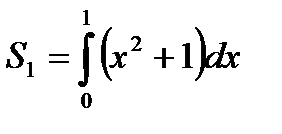 и
и 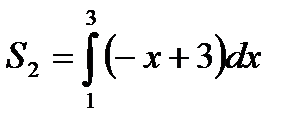 . Получим формулу:
. Получим формулу:
|  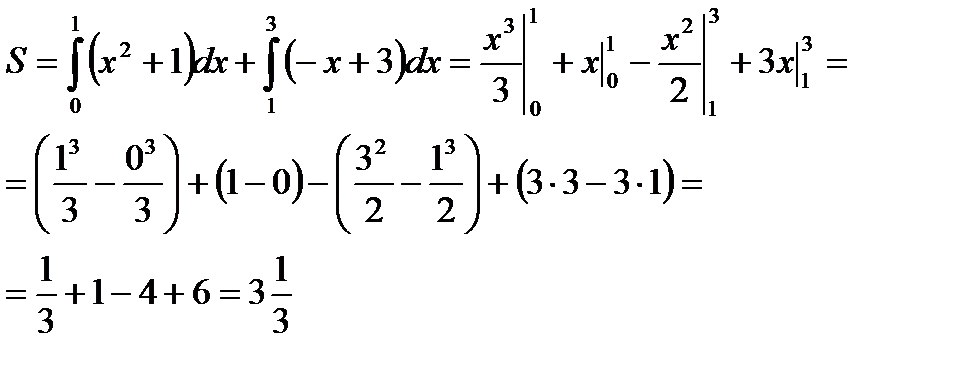 Ответ: Ответ: 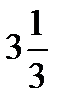 кв.ед. кв.ед. |
Вычисление площадей фигур
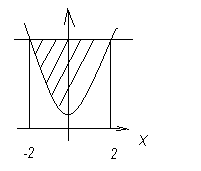
| №1 | №2 | №3 | |||||
|
 |
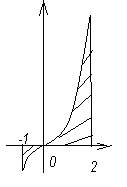 |
Ответы: №1ln3 кв.ед.,№2 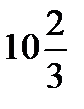 кв.ед.,№3
кв.ед.,№3 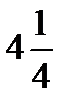 кв.ед.
кв.ед.
Контрольные вопросы:
1. Что называют определённым интегралом?
2. Приведите формулу вычисления определённого интеграла.
3. Перечислить свойства определённого интеграла.
4. Приведите определение криволинейной трапеции.
5. В чём геометрический смысл определённого интеграла?
Практическая работа 2
«Интегрирование подстановкой»
Цель работы: формировать умения по решению основных задач
Выполнить задания