Матричный метод решения системы уравнений. Метод Гаусса.

Методом Гаусса решаются системы линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений ( 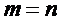), либо отлично от него ( 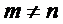). Исключим сначала неизвестное 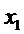из всех уравнений системы, кроме первого. Для этого прежде всего разделим обе части первого уравнения на коэффициент 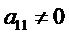; тогда получим новую систему, равносильную данной:

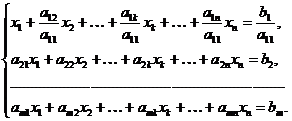
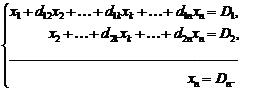
Система вида (13) называется ступенчатой, а система вида (14) – треугольной.

Переход системы (2) к равносильной ей системе (13) или (14) называется прямым ходом метода Гаусса, нахождение неизвестных из последних систем – обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу

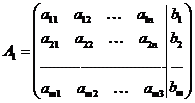, (15)

называемую расширенной матрицей системы (2), так как в ней кроме матрицы системы 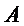, дополнительно включен столбец свободных членов.

7) Векторы. Линейные операции над векторами. Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов.Определение 3.1. Вектором называется направленный отрезок 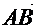с начальной точкой 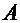и конечной точкой 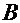(который можно перемещать параллельно самому себе).

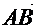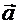Если даны начало вектора (точка А) и его конец (точка В), то вектор обозначается или .Определение 3.1. Длиной (или модулем) 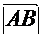вектора 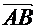называется число, равное длине отрезка 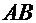, изображающего вектор. Определение 3.2. Нуль-вектором называется вектор, у которого конец совпадает с началом, он обозначается: .

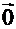Направление нуль-вектора не определено. Можно считать, что нуль-вектор имеет любое желаемое в данный момент направление.

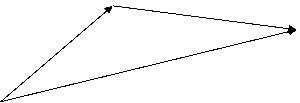
Суммой двух векторов 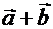называется вектор, полученный по правилу «треугольника»: второй вектор 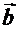откладывается так, чтобы его начало совпало с концом первого вектора .

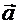Суммой будет являться «замыкающий» вектор 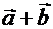, начало которого совпадает с началом первого вектора 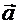, а конец – с концом второго вектора .

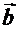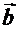
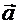
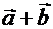
Свойства сложения векторов.

1. Коммутативный закон сложения: .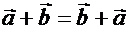

2. Ассоциативный закон сложения: .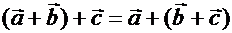

3. .

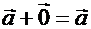Определение 3.6. Противоположным к вектору 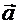называется такой вектор, что его сумма с 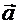равна нуль-вектору.

Противоположный к 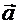вектор обозначается 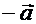: 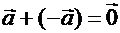. Определение 3.7. Разностью двух векторов 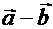называется сумма векторов 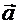и противоположного к 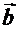: 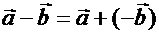. Определение 3.8. Произведением вектора 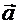на действительное число 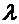называется вектор 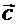, коллинеарный вектору 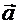имеющий длину 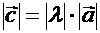, направление которого совпадает с направлением вектора 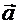, если 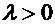, и противоположно ему, если .

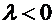Свойства умножения вектора на число.

1. Коммутативный закон: .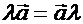

2. Ассоциативный закон: .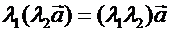

3. Дистрибутивный закон: .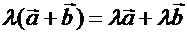

Доказательства этих свойств вытекают непосредственно из определения операции.

Теорема 3.1. Два вектора 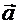и 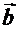коллинеарны тогда и только тогда, когда 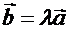или .

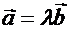Определение 3.9. Единичным называется вектор, длина которого равна единице.

Вектор характеризуется длиной и направлением. Длина вектора (его модуль) вычисляется по формуле (8). Направление вектора в пространстве можно задать углами 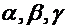, которые составляет вектор с осями координат. Косинусы этих углов 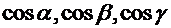называются направляющими косинусами вектора.

Пусть дан вектор 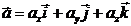. Тогда: 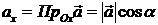; ; 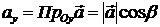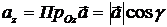, откуда:

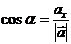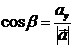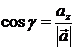; ; . (11)

Подставляя в формулы (11) выражение (8) для 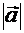, получим:

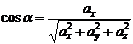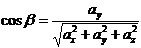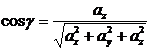; ; (12)

Возводя каждое из выражений (12) в квадрат и складывая, получим:

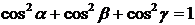. (13)

Таким образом, среди трех углов 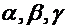независимыми являются только два, а третий определяется из соотношения (13).

Замечание. Вектор в трехмерном пространстве задается тремя скалярными величинами. Это могут быть три координаты или два угла и длина вектора и т.д. Аналогично этому вектор в двумерном пространстве определяется двумя скалярными величинами: двумя координатами или углом и длиной и т.д.

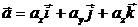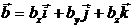Пусть векторы и коллинеарны. В соответствии с теоремой 3.1 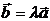или 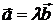, что означает для координат выполнение следующих соотношени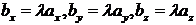й: или 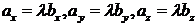. Выразив 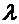из этих равенств и приравняв, получим:

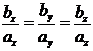или 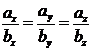. (14)

Таким образом, для того, чтобы два вектора 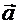и 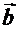были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.