Схема построения графика функции.

Для построения графика функции y=f(x) необходимо определить:

1)область допустимых значений аргумента функции. Четность, нечетность. Периодичность.

2)Асимптоты: а)вертикальные б)наклонные

3)область возрастания и убывания функции. Точки экстремумов.

4)направление выпуклости. Точки перегиба.

5)Точки пересечения с осями координат.

Асимптоты.

Определение: прямая х=х0 называется вертикальной асимптотой графика функции y=f(x),если выполняется хоть одно из условий: 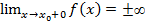или ;

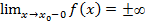Определение: Прямая y=kx+b называется наклонной асимптотой графика функции y=f(x) при х--> 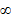(х-->- 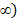,если эта функция представима в виде y=kx+b+α(x) где α(x)à0 при xà (- .

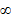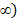Теорема 32 о необходимом и достаточном условии наличия наклонной асимптоты: для того чтобы функция y=f(x) имела наклонную асимптоту при xà 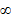(- 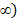необходимо и достаточно, чтобы существовали пределы: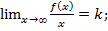

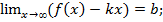
Док-во : Необходимость: предполагается, что график функции y=f(x)имеет наклонную асимптоту: надо доказать, что выполняются соотношения: 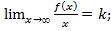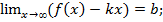По определению, если функция имеет наклонную асимптоту y=kx+b, при х--> 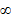,то справедливо представление этой функции в виде: 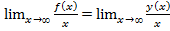= = 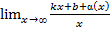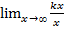+ 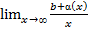=k. 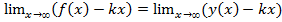= 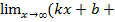α(x)-kx)= 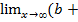α(x))=b- 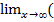α(x))=b. Достаточность: предполагается, что выполняются равенства: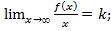 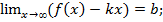Надо доказать, что y=kx+b является наклонной асимптотой Графика функции y=f(x), при х--> 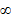.воспользуемся вторым равенством.Док-во :Наличие предела у функции f(x)-kx означает, что f(x)-kx-b= α(x).где α(x) –бесконечно малая при xà 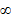функция. Следовательно:f(x)=kx+b+ α(x).

Возрастание и убывание функции в точке.

Определение: функция y=f(x) возрастает (убывает) в точке , если найдется такая окрестность точки , что выполняется: f(x)>f( ) (f(x)<f( ))при x> ;f(x)<f( ) (f(x)>f( ) при x<

Теорема 33.Пусть функция y=f(x) дифференцируема в точке x= и f’( )>0(f’(x)<0)тогда функция f(x) возрастает (убывает) в

Док-во: проведем для случая f’( )>0

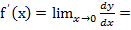
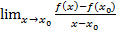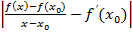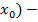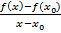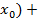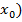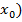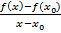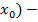По определению наличия производной функции f(x) означает, что следующий предел: тогда в соответствии со вторым определением функции, для любого έ>0 найдется δ>0 такое, что при Іx- І< δ выполняется: < έ; f’( έ< <f’( έ.выберем έ<f’( àf’( - έ>0,тогда >f’( έ>0.

А)f(x)-f( 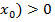при x> Б)f(x)-f( 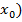<0 при x<

Локальный максимум и минимум функции.

Определение: функция y=f(x) имеет в точке 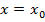локальный макс(мин),если найдется окрестность точки ,в пределах которой значение f( 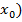является наибольшим(наименьшим) среди всех значений функции в этой окрестности. вместе локальный максимум и минимум получили название локального экстремума.

Теорема 34.

Пусть функция y=f(x)имеет локальный экстремум в точке и дифференцируема в этой точке. Тогда f’( )=0.

Док-во: так как точка локального экстремума не является ни точкой возрастания ни точкой убывания функции, значит не выполняется равенство f’( )>0,f’( )<0,то очевидно, что f’( )=0.

Теорема 35(Ролля).

Пусть функция y=f(x) непрерывна на сегменте 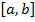и дифференцируема в любой внутренней точке этого сегмента. Пусть кроме того f(a)=f(b).Тогда внутри 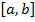найдется точка d , такая, что f’(d)=0.

Док-во: так как функция непрерывна на сегменте 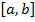,то она достигает на этом сегменте своих наибольшего M и наименьшего m значения. Могут реализоваться 2 случая:

a)значения m и M достигается на краях сегмента. Тогда из условия f(a)=f(b)следует, что M=m,но такое возможно только при f(x)=const.значит найдется точка d такая,что f’(d)=0.

Б)одно из значений m или M достигается на краю отрезка а другое внутри него в некоторой точке d,значит d-точка экстремума и f’(d)=0.

Теорема 36(Логранжа).

Пусть функция f(x) непрерывна на 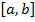и дифференцируема в любой точке внутри сегмента:f(b)-f(a)=f’(d)(b-a)-формула Логранжа. d- точка внутри .

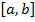Док-во: Построим вспомогательную функцию F(x)=f(x)-f(a)- 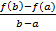(b-a).Эта функция удовлетворяет условиям теоремы Ролля. Действительно, функция непрерывна на 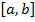.F(a)= 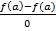- 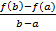(a-a)=0;F(b)=f(b)-f(a)- 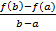(b-a)=0 таким образом F(a)=F(b) Вычислим F'(x):по теореме Ролля найдется точка d такая, что F’(d)=0=f’(d)= 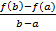àf(b)-f(a)=(b-a)f’(d).