Определители 2го и 3г порядка. Определение. Теоремы разложения и аннулирования

Определители 2го и 3г порядка. Определение. Теоремы разложения и аннулирования

1. Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали:

2. Определителем третьего порядка называется следующее выражение:

Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. правило Саррюса

Определители любого порядка. Свойства определителей.

Сначала опишем основные свойства определителей относительно преобразования матриц. Знание этих свойств поможет упрошать вычисления и находить определители произвольного порядка.

Свойство 1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).

Матрицы. Определение. Действия над матрицами.

Матрицей размерности m x n называется прямоугольная таблицаmxnчисел a _ij , i=1,..., m, j=1,..., n:

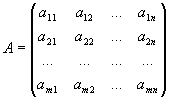
расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n -порядок матрицы).

Линейные матричные операции
По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.
Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

, ,

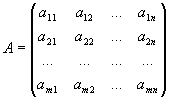то произведением матриц A и B, называется матрица

,

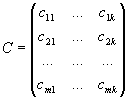Элементы которой вычисляются по формуле

c _ij =a _i1 b _1j + a _i2 b _2j + ... +a _in b _nj , i=1, ..., m, j=1, ..., k.

Произведение матриц A и B обозначается AB, т.е. C=AB.

ПРИМЕР 1. Действия с матрицами.

Произведение матриц, вообще говоря, зависит от порядка сомножителей. Если AB=BA, то матрицы A и B называются перестановочными.

ПРИМЕР 2. Проверка перестановочности матриц.

Для квадратных матриц определена единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули:

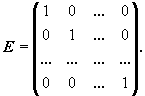
Единичная матрица чаще всего обозначается буквой E или E _n, где n - порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы:

AE=EA=A.

Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица - частный случай скалярной матрицы.

ПРИМЕР 3. Умножение матрицы на матрицы специального вида

Для квадратных матриц определена операция возведения в целую неотрицательную степень:

A ⁰ =E, A ¹ =A, A ² =AA, ..., A ⁿ =A ^n-1 A, ....

ПРИМЕР 4. Возведение матрицы в степень.

Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A ^T:

, .

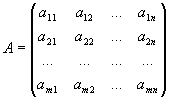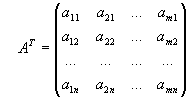Верны соотношения:
(A^T)^T=A;
(A+B)^T=A^T +B^T;
(AB)^T =B^TA^T.

Квадратная матрица A, для которой A ^T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица A называется обратимой, если существует такая матрица X, что
AX=XA=E.
Матрица X называется обратной к матрице A и обозначается A ^-1, т.е.
A A ^-1 =A ^-1A=E.

Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A ^-1.

Верно соотношение:(A^-1)^T=(A^T) ^-1.

Свойства обратной матрицы

§ , где обозначает определитель.

§ для любых двух обратимых матриц A и B.

§ где * ^T обозначает транспонированную матрицу.

§ для любого коэффициента .

ранг матрицы. Базисный минор. Элементарные преобразования матриц. Метод элементарных преобразования для нахождения ранга.

Следующие случаи.

a). Если D¹0, то система (1) имеет единственное решение, которое может

быть найдено по формулам Крамера : x₁=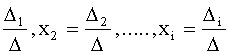

, где

определитель n-го порядка D_i ( i=1,2,...,n) получается из

определителя системы путем замены i-го столбца свободными членами b₁

, b₂ ,..., b_n.

б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

__________________________________________

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

]Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

]Следствия

§ Количество главных переменных системы равно рангу системы.

§ Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Метод Гаусса

Метод Гаусса- классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовате

Получим

(a₁₁*М + a₂₁) x₁ + ... = b₁*M + b₂

Для того, чтобы член при x₁ равнялся нулю, нужно, чтобы M = - a₂₁ / a₁₁. Проделав эту операцию, получившееся уравнение запишем вместо второго и приступим к третьему уравнению. К нему мы прибавим первое уравнение, умноженное на M = - a₃₁ / a₁₁и тоже получим ноль вместо члена при x₁. Такую операцию нужно проделать над всеми остальными уравнениями. В результате получим систему такого вида:

a11x1 +	a12x2 +	a13x3 +	...	a1NxN = b1
	a22x2 +	a23x3 +	...	a2NxN = b2
	a32x2 +	a33x3 +	...	a3NxN = b3
...
	aN2x2 +	aN3x3 +	...	aNNxN = bN

После этого будем избавляться от членов при x₂ в третьем, четвертом, N-ом уравнении. Для этого нужно к уравнению с j-м номером прибавить 2-ое уравнение, умноженное на M = - a_j2 / a₂₂. Проделав эту операцию над всеми остальными уравнениями, получим систему где нет членов с x₂ в уравнениях с номером больше 2.

И так далее... Проделав это для третьего члена, четвертого... до тех пор, пока не кончатся уравнения, получим в итоге систему треугольного вида.

Определители 2го и 3г порядка. Определение. Теоремы разложения и аннулирования

1. Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали:

2. Определителем третьего порядка называется следующее выражение:

Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. правило Саррюса