Экстремумы. Наибольшее и наименьшее значение функции.

В Maple для исследования функции на экстремум имеется команда extrema(f,{cond},x,’s’) , где f- функция, экстремумы которой ищутся, в фигурных скобках {cond} указываются ограничения для переменной, х – имя переменной, по которой ищется экстремум, в апострофах ’s’ – указывается имя переменной, которой будет присвоена координата точки экстремума. Если оставить пустыми фигурные скобки {}, то поиск экстремумов будет производиться на всей числовой оси. Результат действия этой команды относится к типу set. Пример:

> readlib(extrema):

> extrema(arctan(x)-ln(1+x^2)/2,{},x,’x0’);x0;

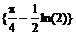
{{x=1}}

В первой строке вывода приводится экстремум функции, а во второй строке вывода – точка этого экстремума.

К сожалению, эта команда не может дать ответ на вопрос, какая из точек экстремума есть максимум, а какая – минимум. Для нахождения максимума функции f(x) по переменной х на интервале 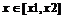используется команда maximize(f,x,x=x1..x2), а для нахождения минимума функции f(x)по переменной х на интервале 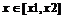используется команда minimize(f, x, x=x1..x2). Если после переменной указать ’infinity’или интервал

x=-infinity..+infinity, то команды maximize и minimize будут искать, соответственно, максимумы и минимумы на всей числовой оси как во множестве вещественных чисел, так и комплексных. Если такие параметры не указывать, то поиск максимумов и минимумов будет производиться только во множестве вещественных чисел. Пример:

> maximize(exp(-x^2),{x});

Недостаток этих команд в том, что они выдают только значения функции в точках максимума и минимума, соответственно. Поэтому для того, чтобы полностью решить задачу об исследовании функции y=f(x) на экстремумы с указанием их характера (max или min) и координат (x, y) следует сначала выполнить команду:

> extrema(f,{},x,’s’);s;

а затем выполнить команды maximize(f,x); minimize(f,x).После этого будут полностью найдены координаты всех экстремумов и определены их характеры (max или min).

Команды maximize и minimize быстро находят абсолютные экстремумы, но не всегда пригодны для нахождения локальных экстремумов. Команда extrema вычисляет так же критические точки, в которых функция не имеет экстремума. В этом случае экстремальных значений функции в первой строке вывода будет меньше, чем вычисленных критических точек во второй строке вывода. Выяснить характер найденного экстремума функции f(x)в точке x=x₀ можно, если вычислить вторую производную в этой точке и по ее знаку сделать вывод: если 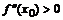, то в точке x₀ будет min, а если 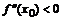- то max.

В последней версии пакета аналитических вычислений Maple 6 описанный выше недостаток команд maximize и minimize устранен. Координаты точек максимума или минимума можно получить, если в параметрах этих команд после переменной записать через запятую новую опцию location. В результате в строке вывода после самого максимума (минимума) функции будут в фигурных скобках указаны координаты точек максимума (минимума). Например:

> minimize(x^4-x^2, x, location);

, { , }

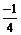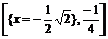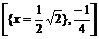В строке вывода получились координаты минимумов и значения функции в этих точках.

Команды extrema,maximize и minimizeобязательно должны быть загружены из стандартной библиотеки командой readlib(name), где name – имя загружаемой команды.

Задание 3.2.

1. Найти max и min .

> readlib(extrema):

> y:=(x^2-1/2)*arcsin(x)/2+x*sqrt(1-x^2)/4-

Pi*x^2/12:

> extrema(y,{},x,'s');s;

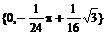
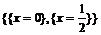
После выполнения этих команд найдены экстремумы функции и точки экстремумов. Порядок следования x–координат экстремумов во второй строке вывода соответствует порядку следования значений экстремумов в первой строке вывода. Таким образом, найдены экстремумы в точках (0,0) и (1/2, –p/24+ 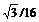). Осталось выяснить, какая из них является максимумом, а какая – минимумом. Для этого используйте команды maximize и minimize.

> readlib(maximize):readlib(minimize):

> ymax:=maximize(y,{x});

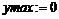
> ymin:=minimize(y,{x});

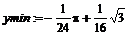
Ответ наберите в текстовом режиме в новой строке:

“Экстремумы: , .”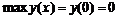

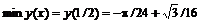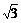Для набора математических символов и греческих букв в текстовом режиме следует нажать кнопку со значком суммы на Панели инструментов. В появившейся строке ввода формул ниже Панели инструментов следует набирать обычные команды Maple,после чего нажать Enter. Например, для отображения формулы следует набрать в строке ввода формул sqrt(3).

Для возвращения в текстовый режим снова следует нажать на кнопку с буквой «Т».

Поэтому порядок набора второй формулы в ответе такой:

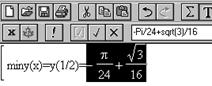
§ находясь в текстовом режиме, набрать: miny(x)=y(1/2)= ;

§ нажать на кнопку

§ в строке ввода формул набрать: -Pi/24+sqrt(3)/16

§ нажать Enter;

§ вернуться в текстовый режим.

2. Найдите наибольшее и наименьшее значение 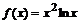на интервале 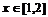. Наберите:

> f:=x^2*ln(x):

> maximize(f,{x},{x=1..2});

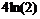
> minimize(f,{x},{x=1..2}):simplify(%);

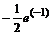
Ответ наберите в текстовом режиме в новой строке:

”Наибольшее значение: 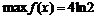, наименьшее значение “.

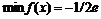3. Найти экстремумы функции 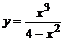и установить их характер с помощью второй производной. Наберите:

> restart:y:=x^3/(4-x^2): readlib(extrema):

readlib(maximize): readlib(minimize):

> extrema(y,{},x,'s');s;

{ }

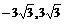{{x=0},{ },{ }}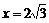

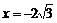Получено два экстремума и три критические точки. Исследование можно продолжить с помощью второй производной:

> d2:=diff(y,x$2): x:=0: d2y(x):=d2;

d2y(0):=0

> x:=2*sqrt(3):d2y(x):=d2;

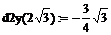
> x:=-2*sqrt(3):d2y(x):=d2;

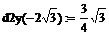
Так как 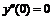, то в точке x=0 нет экстремума; так как 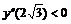, то в точке 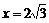будет max; так как 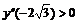, то в точке 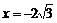будет min. Перейдите в текстовый режим и запишите ответ в виде:

“Максимум в точке ( 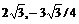), минимум в точке ( )”.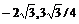