Общий случай полиномиального интерполирования.

Метод неопределенных коэффициентов

Полином Q_m(x)=a₀+a₁x+…+a_mx^m называется интерполяционным для данной функции f(x) если в заданных точках x_i (i = 1,2,…,n) он принимает те же значения, что и функция f(x), т.е. имеет место равенство Q_m(x_i)=f(x_i). Интерполяционный полином, принимающий в заданных точках x₀,x₁,…,x_n те же значения, что и f(x) всегда единственен. Степень интерполяционного полинома определяется как m=n-1, где n - число экспериментальных точек. Таким образом, для данной экспериментальной зависимости, состоящей из 5 точек, степень интерполирующего полинома равна 4, т.е. искомая функция имеет вид Q₄(x)=a₀+a₁x+a₂x²+a₃x³+a₄x⁴. Неизвестные коэффициенты полинома а₀, а₁, а₂, а₃, а₄ можно определить из системы уравнений

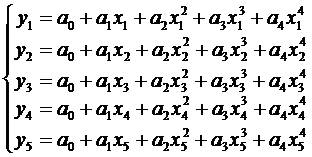Выполним интерполяцию заданной табличной зависимости, используя средства электронных таблиц Excel. Вначале снова построим график табличной зависимости в форме точечной диаграммы. При построении графика ряд данных формируется указанием сразу всех координат экспериментальных точек. График может быть построен более быстро, если перед вызовом Мастера Диаграмм предварительно выделить диапазон ячеек $B$3:$F$4.

Интерполяционный полином построим выполнив Меню Диаграмма - Добавить линию тренда. В появившемся окне Линия Тренда во вкладке Тип выберем Полиномиальная, Степень 4. Во вкладке Параметры снова поставим флажок Показывать уравнение на диаграмме. Результат представлен на рис.11.

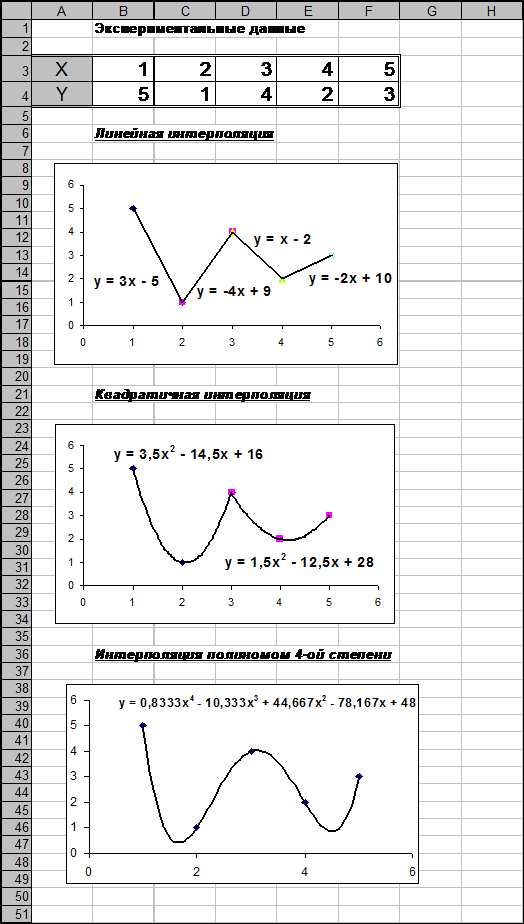
Рис. 11

Аппроксимация функций

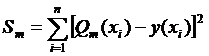Полином Q_m(x)=a₀+a₁x+…+a_mx^m называется аппроксимирующим заданную функцию y(x), если он имеет наименьшее отклонение от заданной функции y(x). Максимальная степень m аппроксимирующего полинома, как правило, всегда значительно меньше числа экспериментальных точек. За меру отклонения полинома Q_m(x)=a₀+a₁x+…+a_mx^m от функции y(x) принимают величину

где S_m есть функция от неизвестных коэффициентов а₀, а₁, …, а_m, которые нужно подобрать так, чтобы величина S_m была минимальной. Этот метод носит название метода наименьших квадратов.

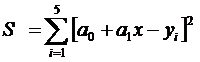Аппроксимируем заданную табличную зависимость полиномом 1-й степени. Аппроксимирующий полином будет иметь вид Q(x)=a₀+a₁x. Величина

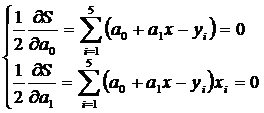должна быть минимальна, а значит, должно быть выполнено условие равенства нулю всех ее частных производных, т.е.

Таким образом, получаем систему из 2-х линейных уравнений, позволяющий найти неизвестные коэффициенты а₀, а₁:

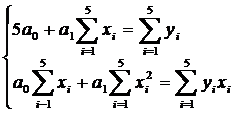Выполним аппроксимацию полиномом 1-ой степени, используя средства электронных таблиц Excel. Построим график табличной зависимости. Для этого выделим всю таблицу значений и далее на этом диапазоне ячеек построим точечную диаграмму. Искомый аппроксимирующий полином построим выполнив Меню Диаграмма - Добавить линию тренда. В появившемся окне Линия Тренда во вкладке Тип выберем Линейная, во вкладке Параметры снова поставим флажок Показывать уравнение на диаграмме. Результат представлен на рис. 12.

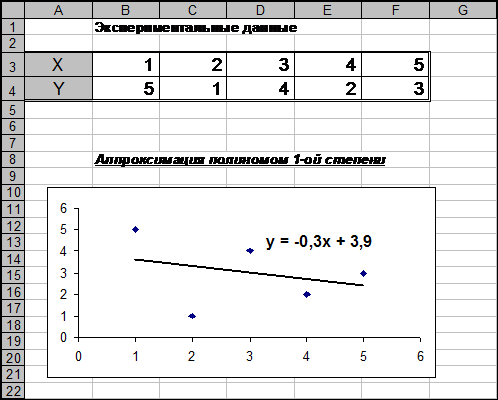
Рис. 12