Общий случай подвижной границы

Очевидно, что подвижная граница не обязательно должна быть вертикальной прямой: если экстремаль имеет дополнительную степень свободы, то естественно допустить, что она может принадлежать любой кривой (не исключается случай вертикальной и горизонтальной прямой).

Рассмотрим задачу в общей постановке.

Пусть в вариационной задаче об отыскании экстремума функционала

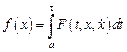(10)

одна граничная точка фиксирована 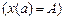, а вторая – 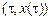– может перемещаться по некоторой кривой 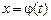. Тогда класс кривых, на которых ищется экстремум, расширяется, но вариационная задача остается содержательной. Функционал в этом случае начинает зависеть, вообще говоря, от трех переменных: функции 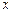и параметров .

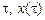Пусть 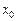– экстремаль, удовлетворяющая граничным условиям 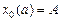, 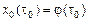; здесь 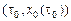– вторая граничная точка. В силу необходимого условия экстремума 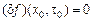. Вычисляя вариацию функционала (10), получаем:

.

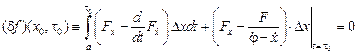Полагая 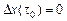, получаем, что должно быть выполнено основное необходимое для достижения экстремума в задаче с неподвижными границами условие – функция 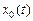является решением уравнения Эйлера. Значит, на функции 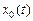уравнение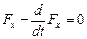

обращается в тождество. А тогда в формуле для вариации функционала (10) первое интегральное слагаемое обращается в нуль и вариация приобретает вид

.

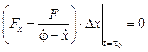Теперь положим 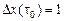, получим следующее условие

,

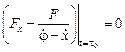которому, если 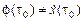(то есть экстремаль пересекает кривую 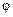, а не касается ее!), удобнее придать вид:

.

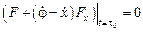Полученное равенство называется условием трансверсальности.

Аналогичное условие возникнет и на левом конце, если ему разрешить меняться на какой-нибудь кривой.

Замечание. Условию трансверсальности часто удается придать простой геометрический смысл: например, для функционалов вида

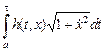(11)

(функция 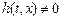), имеем:

.

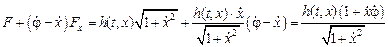Отсюда следует, что условие трансверсальности эквивалентно требованию

,

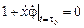что означает ортогональность кривых 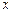и 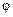в точке их пересечения.

Итак, для решения вариационной задачи с подвижной границей следует:

1. Решить уравнение Эйлера, определив тем самым семейство экстремалей, зависящих от двух произвольных постоянных.
2. Используя условия жесткого закрепления (если они есть), получитьсоотношение для определения произвольных постоянных.
3. С учетом вида множества, которому принадлежит подвижная граница, найти дополнительные соотношения для определения произвольных постоянных.

Пример 7. Исследовать на экстремум функционал

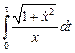
при условии 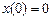, а вторая граница принадлежит прямой .

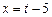Решение. Во-первых, составим и решим уравнение Эйлера. Данный функционал имеет специальный вид: функция 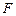не зависит от переменной 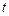. Следовательно, уравнение Эйлера допускает первый интеграл

,

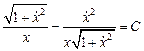представляющий собой дифференциальное уравнение первого порядка, не разрешенное относительно производной. Разрешая его относительно 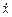, получаем уравнение в разделяющихся переменных

,

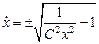интегральными кривыми которого являются окружности

.

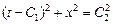Во-вторых, учтем первое граничное условие 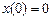. Получим .

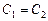В-третьих, множество, которому принадлежит свободная граница, представляет собой кривую, значит, нужно использовать условие трансверсальности, но наш функционал имеет вид (11) и для него, согласно вышеприведенному замечанию, условие трансверсальности совпадает с условием ортогональности. Следовательно, прямая 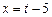должна быть ортогональна окружности, что возможно только тогда, когда прямая лежит на диаметре окружности .

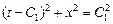Значит, центр этой окружности находится в точке (5,0) пересечения прямой 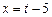с осью .

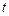Итак, экстремалями данной задачи являются две ветви окружност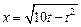и: и 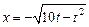(рис.2).