Определение коэффициента истечения из отверстия

И насадок различной формы

Цель работы: экспериментальное определение коэф­фициентов истечения жидкости φ, ε, ξ и μ дляразличных условий истечения.

Теоретическое введение

Отверстие в стенке сосуда, через которое происходит ис­течение жидкости, считается малым, если оно одновременно удовлетворяет двум условиям:

1) Скорость подхода жидкости к отверстию истечения пренебрежимо мала, что имеет место при Ω / F₀ > 4,0, где Ω – площадь подходного живого сечения; F₀ – площадь отверстия.

2) Скорости движения частиц жидкости в верхней и нижней точках отверстий примерно одинаковы. Это условие выполняется в случае, если d / H 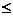0,1, где d – диаметр отверстия; Н – заглубление центра тяжести отверстия под горизонтом жидкости в сосуде.

Как показывают опыты, картина истечения жидкости из некоторого сосуда через малое круглое отверстие в вертикаль­ной тонкой стенке имеет вид, изображенный на рис. 31, где Р₀ – давление на поверхности жидкости в сосуде; F_c – площадь поперечного сечения струи в некотором сечении С–С, называемом сжатым сечением; Q – расход жидкости.

При выходе из отверстия струя по сечению С–С сжимается, что обусловлено инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям.

Согласно опытам расстояние от внутренней поверхности стенки сосуда до сжатого сечения составляет

L₀ ≈ 0,5 ∙ d (1)

Величина 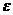называется коэффициентом сжатия струи.

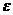= F_c / F₀ (2)

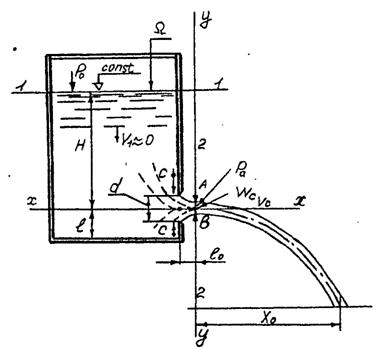
Рис. 31 – Схема истечения свободной незатопленной струи

На участие струи внутренней поверхности стенки сосуда до сечения С–С имеется резко изменяющееся движение; в сече­нии С–С и далее – плавно изменяющееся движение. К сжатому сечению (в связи с равномерным распределением скоростей по сечению) применимо уравнение Бернулли, пользуясь которым, можно определить расход жидкости Q и среднюю скорость V_c в сечении С–С. Соединив уравнением Бернулли два сечения 1–1 и 2–2, из них первое намечаем на уровне жидкости в сосуде и вто­рое – по линии С–С. Плоскость сравнения 0–0 проведем на уров­не центра тяжести площади Х–Х.

Уравнение Бернулли имеет вид:

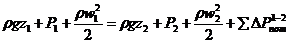, (3)

где 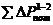– потери энергии между сечениями 1–1 и 2–2, обусловленные в данном случае только сужением струи, т.е. местным сопротивлением.

С учетом того, что w₁ ≈ 0 (скорость жидкости в сечении 1–1 пренебрежимо мала), а также z₁ – z₂ = H и p₁ ≈ p₂ (оба сечения сообщаются с атмосферой, и разность атмосферных давлений на уровне этих сечений невелика ввиду малости плотности воздуха по сравнению с плотностью жидкости), уравнение (3) может быть записано в виде:

.

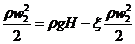Тогда действительная скорость истечения (м/с) жидкости из отверстия

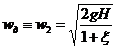. (4)

Скорость, которую имела бы истекающая жидкость при отсутствии потерь энергии на местное сопротивление, называется теоретической скоростью истечения. При ξ = 0 из (4) получаем формулу Торричелли:

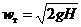(5)

Введя безразмерную величину

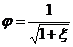, (6)

можно записать

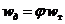, (7)

где j – коэффициент скорости, который может быть определен опытным путем в результате измерения координат точек струи и использования уравнения ее траектории.

Объемный расход (м³/с) вытекающей жидкости может быть выражен через скорость жидкости в сжатом сечении струи и площадь этого сечения:

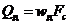. (8)

Теоретический расход может быть достигнут, если бы жидкость с теоретической скоростью вытекала струей с диаметром, равным диаметру отверстия.

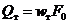. (9)

Отношение действительного расхода к теоретическому называется коэффициентом расхода:

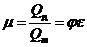. (10)

Отношение действительного расхода к теоретическому называется коэффициентом расхода:

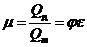. (11)

Этот коэффициент учитывает потери напора, и степень сжатия струи, истекающей из отверстия. Степень сжатия струи в свою очередь зависит от расположения отверстия относительно боковых стенок и дна сосуда. В зависимости от удаления отвер­стия от боковых стенок и дна сосуда различают совершенное, а также неполное сжатие струи.

Совершенное сжатие струи возникает, когда боковые стенки и дно сосуда практически не влияют на истечение. Усло­вием совершенного сжатия является удаленность отверстия на расстояние L > 3d от стенок и дна сосуда, тогда последние не влияют на форму струи и характер истечения. Степень сжатия в этом случае будет наибольшей.

При несоблюдении условия L > 3d , т.е. когда отверстие расположено сравнительно близко к боковой стенке или дну со­суда, сжатие струи получается несовершенным.

В этом случае величина коэффициента сжатия зависит от расположения отверстия относительно дна сосуда или его сте­нок. Чем ближе отверстие расположено к дну или стенкам, тем меньше сжатие и, следовательно, тем больше величина ε.

Приложив к этой материальной частице истекающей жидкости уравнения движения, известные из теоретической механики:

; ,

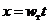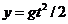где t – время, х, у – текущие координаты струи.

Получим (после совместного решения уравнений движения) уравнение траектории материальной частицы, движущейся со скоростью :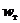

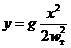_. (12)

Решая совместно уравнение (12) и 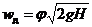, определяют, что

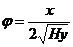(13)

Пользуясь (13), можно вычислить величину коэффициента скорости, если предварительно, опытным путем, определить координаты x и y какой-либо точки траектории струи.

Коэффициент сопротивления отверстия может быть вы­ражен через коэффициент скорости следующим образом:

.

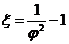В процессе проведения опыта действительный расход воды определяется при помощи мерного цилиндра. Измерив се­кундомером время истечения τ определенного объема воды W, можно вычистить действительный расход из выражения:

Q_д = W/ .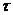

Насадки. Струя жидкости, входя в насадку, вначале подвергается сжатию также как и при истечении из отверстия, но потом постепенно расширяется, заполняет насадку и вытекает из нее полным сечением (рис. 32).

В месте расположения сжатого сечения образуются зоны, заполненные вихревым движением жидкости, отчего потери в насадке значительно возрастают, вследствие увеличения потерь скорость выхода жидкости из насадки меньше скорости истечения из отверстия. Однако, увеличение сечения струи приводит к тому, что, несмотря на пониженную скорость истечения, расход жидкости при истечении через насадку существенно больше, чем при истечении через отверстие.

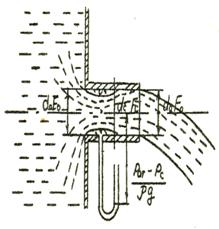
Рис. 32.Истечение из цилиндрического и насадка

Если сделать насадку конически суживающейся, то, бла­годаря уменьшению размеров застойных зон, потери энергии по сравнению с насадкой цилиндрической уменьшаются, вследствие чего скорость истечения увеличивается.

С другой стороны с увеличением угла конусности сжа­тие струи на выходе растет. Вследствие этого имеется опти­мальный угол конусности равный 13° 24', при котором расход жидкости оказывается максимальным. При правильном конструктивном выполнении конически суживающееся насадки расход жидкости, при одинаковом сечении выходного отверстия, существенно превосходит расход через насадку цилиндрической формы.

Максимальный расход жидкости дает конически расши­ряющаяся насадка, которая, вследствие значительных разреше­ний, устанавливающихся в узком сечении, как бы подсасывает жидкость из сосуда.

Во избежание отрыва струи от стенок угол расширения конической насадки не должен превышать некоторого предела 6–7°.

Скорость выхода из конической расширяющейся насадки вследствие увеличенного сечения выхода сравнительно неве­лика. Из-за значительного расширения потока, происходящего в насадке, потери энергии весьма велики. Конически расходящие­ся насадки приводят к торможению и распылению струи.

Таким образом, насадки всех видов в большей или меньшей степени уменьшают скорость истечения вследствие увеличения гидравлических потерь при выходе. С другой сторо­ны, в результате увеличения поперечного сечения выходящей струи, расход жидкости при истечении через насадки больше, чем при истечении через отверстие с таким же поперечным се­чением.

В данной работе рассматриваются три типа насадок, коэффициенты истечения которых, даны в таблице 1:

Таблица 1

Коэффициенты истечения для отверстий и насадок

Тип отверстия или насадка	j	e	m	ξ
Насадок конический сходящийся	0,96	0,98	0,94	0,09
Внешний цилиндрический насадок	0,82	1,0	0,82	0,5
Насадок конический расходящийся	0,45-0,5	-	0,45-0,5	3,94-3

Основные расчетные зависимости для насадок остаются теми же, что и для случая истечения жидкости из отверстия.

Для того, чтобы рассматриваемая, весьма короткая ци­линдрическая труба «работала», как насадка (без отрыва тран­зитной струи от боковых стенок и в условиях, когда потери на­пора по длине получаются пренебрежительно малыми) требует­ся соблюдение следующих двух условий:

1. Длина насадки должна быть ограничена следующими пределами

(3,5 – 4,0) d 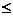L_н 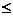H < (6,0 – 7,0) d,

где d – диаметр отверстия насадки.

При L_н < (3,5 – 4,0) d длина насадки может оказаться не­достаточной для расширения транзитной струи после сжатия на входе, т.е. возможен «проскок» струи через насадку (отрыв по­тока от боковых стенок трубы).

При L_н > (6,0 – 7,0) d потери набора по длине соизмери­мы с местными потерями, т.е. имеет место случаи «короткого» трубопровода, когда необходимо учитывать, как местные поте­ри, так и потери напора по длине.

2. Максимальная величина вакуума при истечении в ат­мосферу в тонкой стенке.

Благодаря вакууму насадка дополнительно подсасывает жидкость, что и приводит к увеличению его производительно­сти, несмотря на увеличение потерь напора.

Основные расчетные зависимости для насадок остаются те же, что и для случая истечения жидкости из отверстия.

,

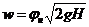где w – средняя скорость в выходном сечении насадки; φ_н – коэффициент скорости для насадки.

,

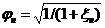где ξ_н – полный коэффициент сопротивления насадка, учитывающего потери внутри насадка.