Теоремы ферма, ролля, лагранжа, коши
ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА, КОШИ
ТЕОРЕМА ФЕРМА. (О равенстве нулю производной)
утверждает, что любая действительная дифференцируемая функция, принимающая одинаковые значения на концах интервала, должна иметь в этом интервале хотя бы одну стационарную точку, т.е. точку, в которой первая производная равна нулю.Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
ТЕОРЕМА РОЛЛЯ. (О нуле производной функции, принимающей на концах отрезка равные значения) Пусть функция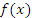 
дифференцируема в открытом промежутке 
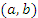, на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения: 
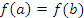. Тогда существует точка 
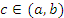, в которой производная функции 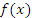равна нулю: 
.
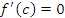Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Следствие.
Если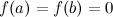 
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
ТЕОРЕМА ЛАГРАНЖА. (О конечных приращениях)
Пусть функция 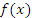дифференцируема в открытом промежутке 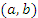и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 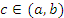, что
  |
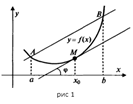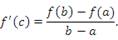Следствие. (Геометрический смысл теоремы Лагранжа)
На кривой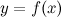 
между точками 
и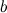 
найдется точка 
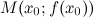, такая, что через эту точку можно провести касательную, параллельную хорде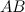 
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
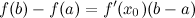
ТЕОРЕМА КОШИ. (Об отношении конечных приращений двух функций
Если функци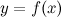и и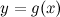 
:
1. непрерывны на отрезке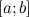 
;
2. дифференцируемы на интервале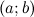 
;
3. производная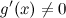 
на интервале ,
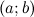тогда на этом интервале найдется по крайней мере одна точка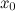 
, такая, что
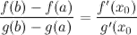
Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.
Теорема
Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.
ПРИЗНАК МОНОТОННОСТИ ФУНКЦИИ
ПЕРВООБРАЗНАЯ, ТЕОРЕМА ОБ ОБЩЕМ ВИДЕ ПЕРВООБРАЗНЫХ К ДАННОЙ ФУНКЦИИ (ВЫВОД). ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ПЕРВООБРАЗНОЙ.
(Об общем виде первообразной для функции)
9. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ СВОЙСТВА.
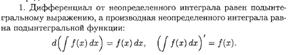
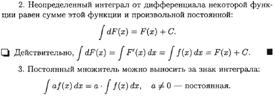
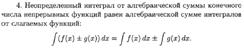
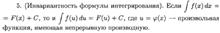
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
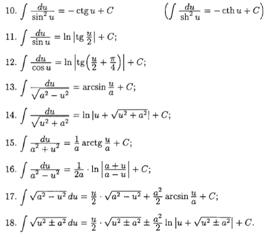
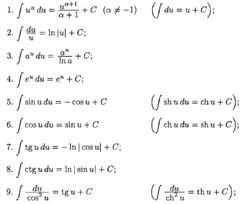
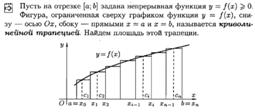
ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ (ВЫВОД). ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ИНТЕГРАЛА.
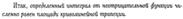
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
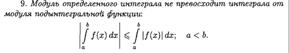
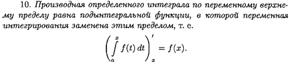
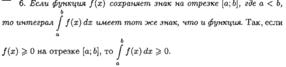
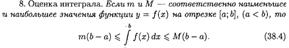
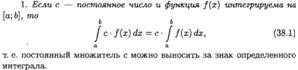
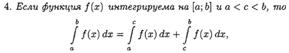
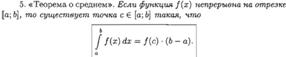
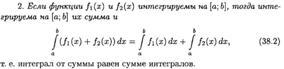
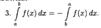
ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ (ВЫВОД, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ). ЧТО НАЗЫВАЕТСЯ СРЕДНИМ ЗНАЧЕНИЕМ ФУНКЦИИ НА ОТРЕЗКЕ?
ПРОИЗВОДНАЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПО ВЕРХНЕМУ ПРЕДЕЛУ (ВЫВОД).
16. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
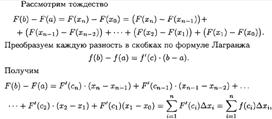
17. ФОРМУЛА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ ДЛЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
18. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
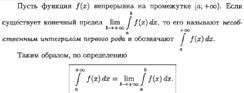
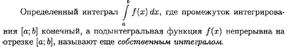
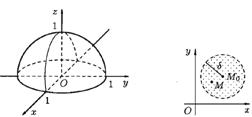
19. ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ГРАФИК ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ.
ОБЩИЙ ВИД ЛИНЕЙНОГО ДУ N-ГО ПОРЯДКА. ЛИНЕЙНОЕ ОДНОРОДНОЕ ДУ 2-ГО ПОРЯДКА. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ. МОЖЕТ ЛИ НУЛЕВОЕ РЕШЕНИЕ ВХОДИТЬ В ФУНДАМЕНТАЛЬНУЮ СИСТЕМУ РЕШЕНИЙ? СКОЛЬКО ФУНДАМЕНТАЛЬНЫХ СИСТЕМ РЕШЕНИЙ ИМЕЕТ ТАКОЕ ДУ?
СТРУКТУРА ОБЩЕГО РЕШЕНИЯ ЛИНЕЙНОГО НЕОДНОРОДНОГО ДУ 2-ГО ПОРЯДКА. В КАКИХ СЛУЧАЯХ, И В КАКОМ ВИДЕ МОЖЕТ БЫТЬ НАЙДЕНО ЧАСТНОЕ РЕШЕНИЕ ЛИНЕЙНОГО НЕОДНОРОДНОГО ДУ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ МЕТОДОМ ПОДБОРА ЧАСТНОГО РЕШЕНИЯ?
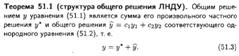
ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА, КОШИ
ТЕОРЕМА ФЕРМА. (О равенстве нулю производной)
утверждает, что любая действительная дифференцируемая функция, принимающая одинаковые значения на концах интервала, должна иметь в этом интервале хотя бы одну стационарную точку, т.е. точку, в которой первая производная равна нулю.Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
ТЕОРЕМА РОЛЛЯ. (О нуле производной функции, принимающей на концах отрезка равные значения) Пусть функция 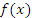дифференцируема в открытом промежутке 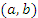, на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения: 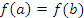. Тогда существует точка 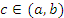, в которой производная функции 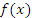равна нулю: .
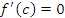Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Следствие.
Если 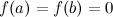, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
ТЕОРЕМА ЛАГРАНЖА. (О конечных приращениях)
Пусть функция 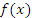дифференцируема в открытом промежутке 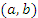и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 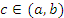, что
| |
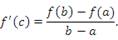Следствие. (Геометрический смысл теоремы Лагранжа)
На кривой 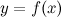между точками и 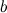найдется точка 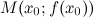, такая, что через эту точку можно провести касательную, параллельную хорде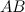
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
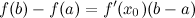
ТЕОРЕМА КОШИ. (Об отношении конечных приращений двух функций
Если функци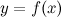и и :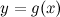
1. непрерывны на отрезке ;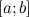
2. дифференцируемы на интервале ;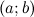
3. производная 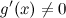на интервале ,
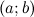тогда на этом интервале найдется по крайней мере одна точка 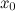, такая, что
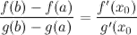
Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.
Теорема
Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.