Критерий прочности Губера – Мизеса

Выделим в окрестности точки тела бесконечно малый параллелепипед, рёбра которого параллельны осям декартовой системы координат (рис. 3.1). В общем случае на гранях этого параллелепипеда будут действовать нормальные напряжения 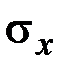, , 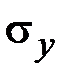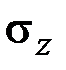и касательные напряжения 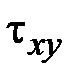, , 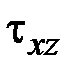, , 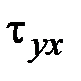, 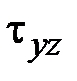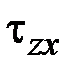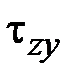(рис. 3.1, а). Из данных величин можно составить матрицу напряжений

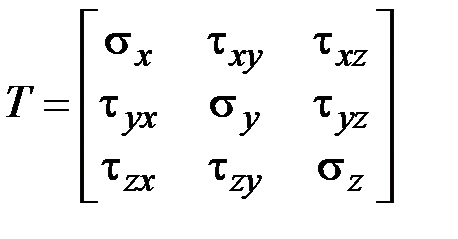, (3.1)

элементы которой называются компонентами тензора напряжений в данной системе координат. По закону парности касательных напряжений

, , .

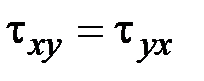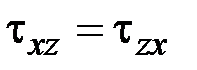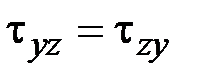Поэтому матрица напряжений (3.1) является симметрической:

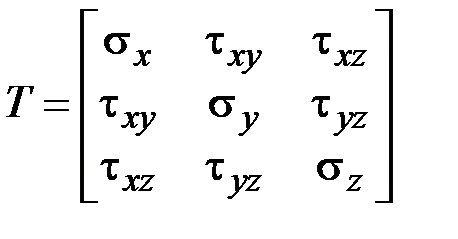. (3.2)

У неё только шесть независимых элементов.

Рис. 3.1. Напряжённое состояние в точке тела:
а – общий случай; б – случай всестороннего сжатия

Сумма диагональных элементов любой матрицы 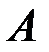называется следом матрицы и обозначается через . Матрица с нулевым следом называется девиатором и обозначается через . Корень квадратный из суммы квадратов всех элементов матрицы 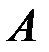называется её нормой и обозначается как 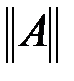. Например, для матрицы (3.2)

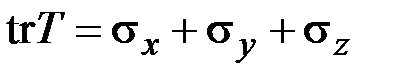, (3.3)

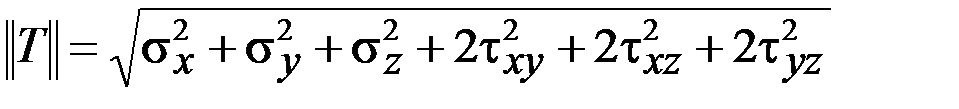. (3.4)

Следует подчеркнуть, что все введённые здесь понятия имеют смысл для любой матрицы, а не только для матрицы напряжений.

Величина

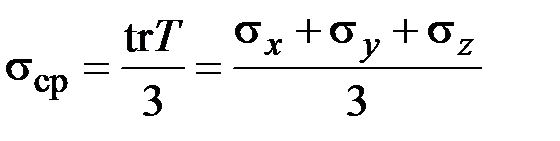(3.5)

называется средним напряжением. Используя единичную матрицу

,

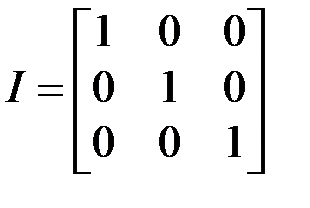след которой 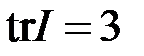, матрицу (3.2) можно представить в виде

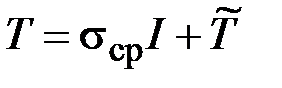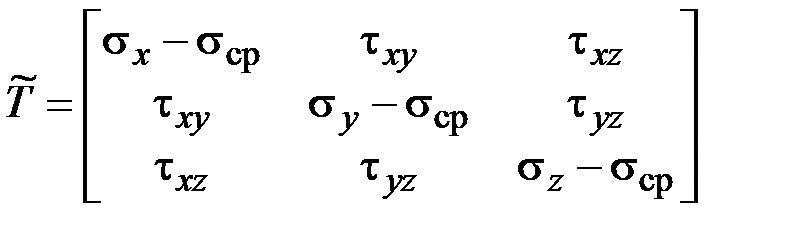, . (3.6)

Поскольку

,

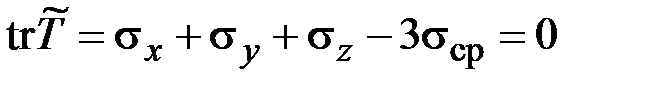матрица 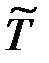в (3.6) является девиатором матрицы напряжений. Очевидно, что у матрицы 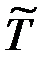только пять независимых элементов.

При всестороннем сжатии (рис. 3.1, б) матрица напряжений имеет вид

,

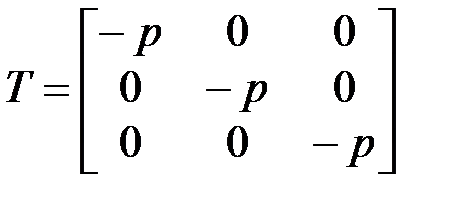где 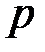– гидростатическое давление (при всестороннем растяжении 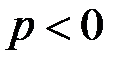). При этом все элементы девиатора матрицы напряжений (3.6) равны нулю. Как показывает опыт, при таком виде нагружения любой материал деформируется упруго. Поэтому переход в пластическое состояние может произойти только при отличном от нуля девиаторе матрицы напряжений .

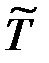По условию пластичности Губера – Мизеса (четвёртой теории прочности)

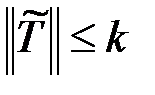, (3.7)

где 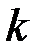– некоторая постоянная. Когда в (3.7) выполняется строгое неравенство, материал деформируется упруго. Знак равенства соответствует предельному состоянию начала пластического деформирования.

Критерий прочности (3.7) допускает простую геометрическую интерпретацию. Для любого напряжённого состояния в данной точке тела девиатору матрицы напряжений 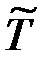можно поставить в соответствие вектор напряжений 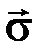с пятью независимыми компонентами, длина которого 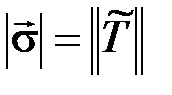. Пока приложенные к телу нагрузки таковы, что конец вектора 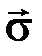находится внутри сферы радиусом 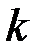(рис. 3.2, а), имеет место упругое состояние. Когда по мере увеличения приложенных нагрузок конец вектора 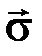достигает сферы радиусом 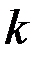(рис. 3.2, б), наступает предельное состояние в данной точке тела.

б)

а)

Рис. 3.2. Интерпретация условия пластичности Губера – Мизеса

Чтобы определить значение постоянной 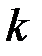для данного материала, достаточно провести испытания на растяжение (рис. 3.3), при которых

, , .

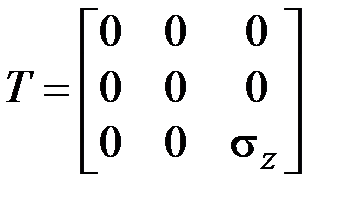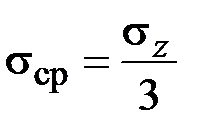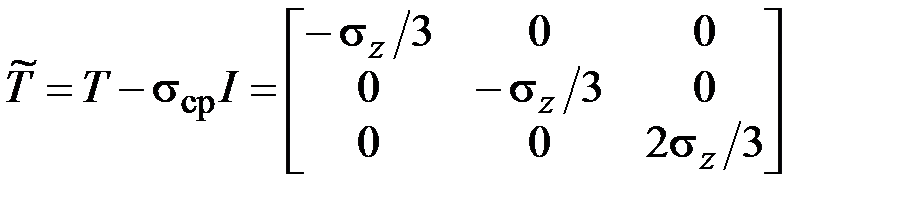Рис. 3.3. Испытание образца материала на одноосное растяжение

Отсюда получаем

.

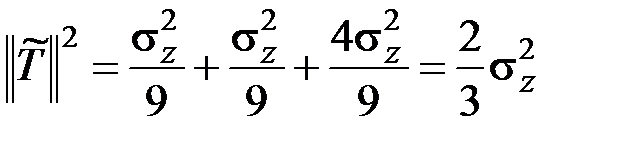Следовательно, для предельного состояния в соответствии с (3.7)

.

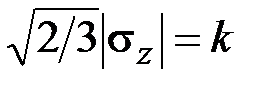С другой стороны, наступление пластического состояния при одноосном растяжении (сжатии) характеризуется пределом текучести :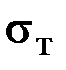

.

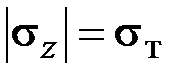Сравнивая последние два равенства, находим

.

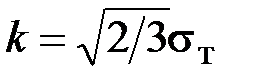Это позволяет переписать критерий (3.7) в виде

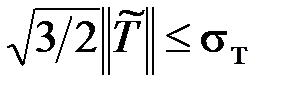. (3.8)

В сопротивлении материалов левая часть (3.8) называется[2] эквивалентным напряжением 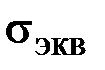, а правая часть – допускаемым напряжением :

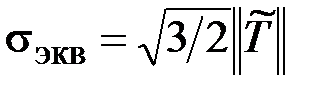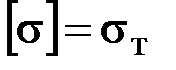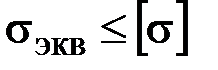, , . (3.9)

В то же время по ряду причин допускаемое напряжение нельзя принимать равным пределу текучести (необходимо иметь некоторый запас прочности на случай возможных перегрузок в процессе эксплуатации, неточного изготовления детали, отклонения свойств применяемого материала от тех свойств, которые установлены при испытании образца и т. д.). Поэтому для пластических материалов принимают следующее значение допускаемого напряжения:

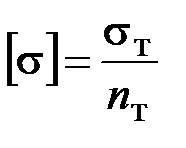, (3.10)

где 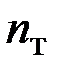– коэффициент запаса прочности по отношению к пределу текучести; этот коэффициент всегда больше, чем единица. Например, в строительных машиностроительных конструкциях обычно 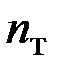= 1.5.

Таким образом, в общем случае напряжённого состояния критерий прочности имеет вид

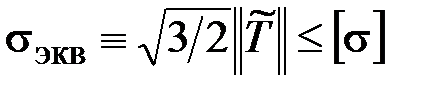. (3.11)

3.2. Формулировка критерия прочности
для частных случаев напряжённого состояния стержня

Для суждения о прочности стержня необходимо знать вид напряжённого состояния в наиболее опасной точке. В общем случае стержень подвергается растяжению (сжатию), кручению и изгибу. При этом в поперечных сечениях стержня возникают нормальные напряжения 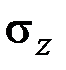от нормальной силы и изгибающих моментов, определяемые формулой Навье (2.53), и касательные напряжения 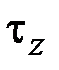от крутящего момента и перерезывающих сил (рис. 3.4).

Рис. 3.4. Напряжённое состояние в точке стержня

В данном напряжённом состоянии

, , .

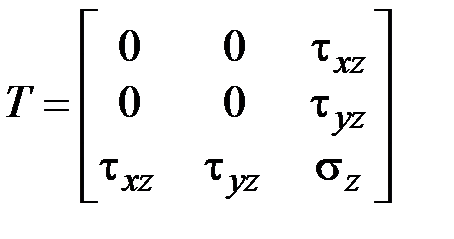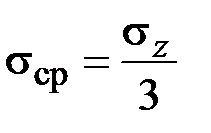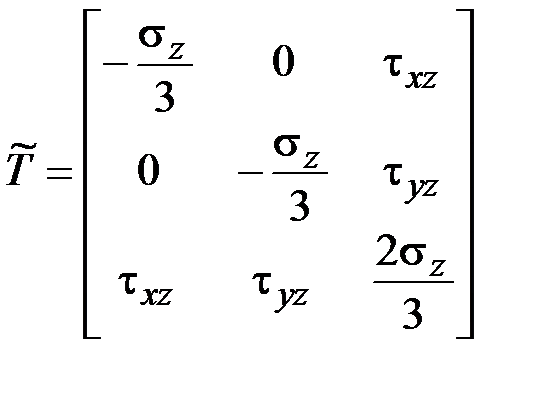Поэтому

,

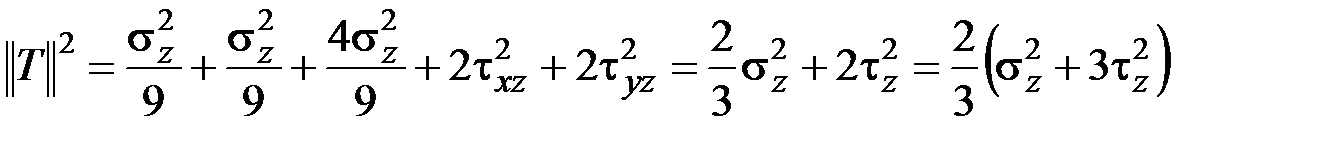где 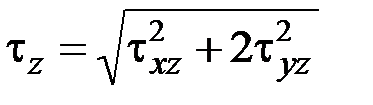– полное касательное напряжение в сечении
(рис. 3.4). Подставив полученное значение

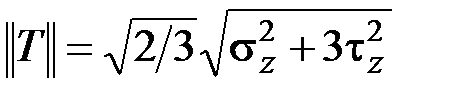
в общее условие прочности (3.11), будем иметь

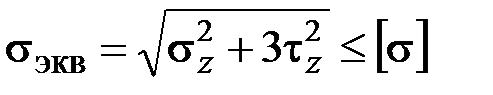. (3.12)

Детализируем условие прочности (3.12) применительно к частным случаям напряжённого состояния, наиболее часто встречающимся на практике. Для упрощения записи конечных выражений введём обозначения

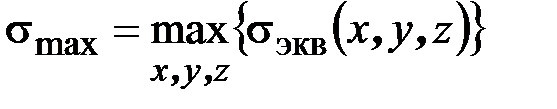
для эквивалентного напряжения в наиболее опасной точке стержня,

, ,

,

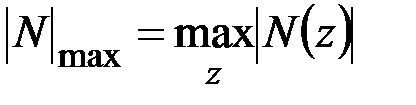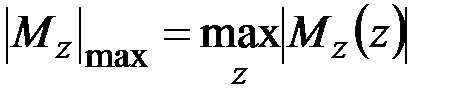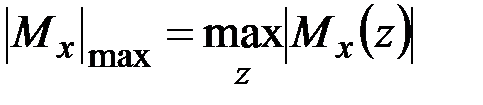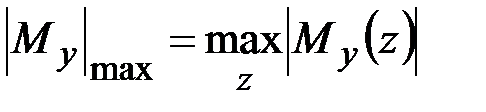
для наибольших абсолютных значений продольной (нормальной) силы, крутящего и изгибающих моментов в поперечных сечениях стержня.

Растяжение-сжатие стержня. В данном случае согласно (2.53)

, , .

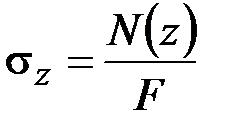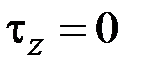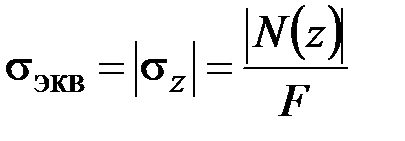Поэтому

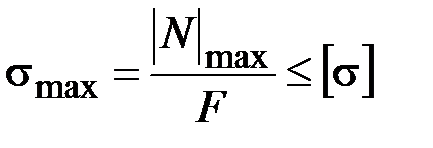. (3.13)

Кручение стержня. В данном случае по формуле (2.56)

, , .

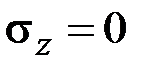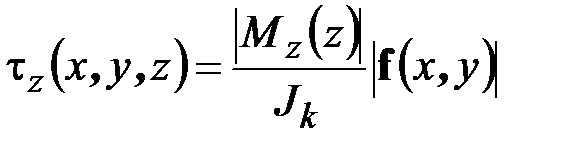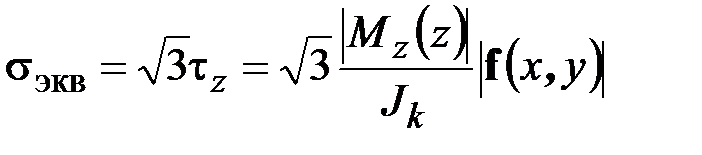Следовательно,

.

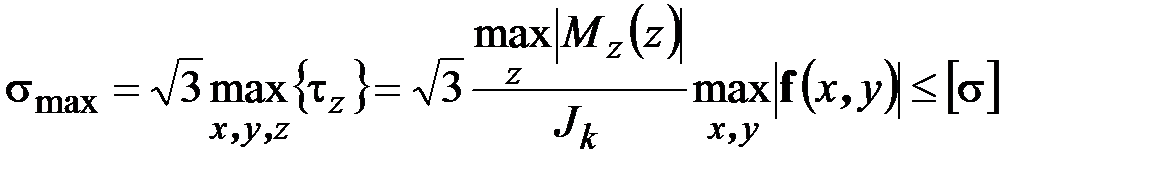Величина

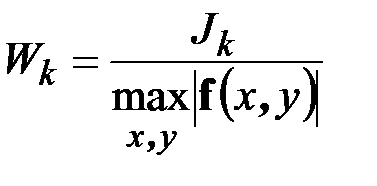(3.14)

называется моментом сопротивления сечения стержня при кручении.
Поэтому

.

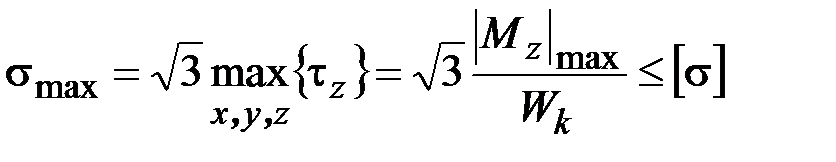Данное выражение можно переписать в виде

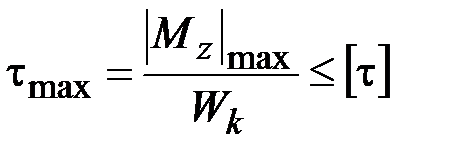, (3.15)

где

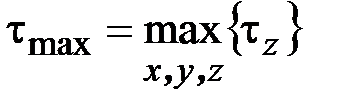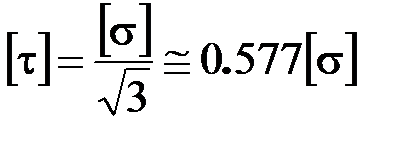, (3.16)

– модуль полного касательного напряжения в опасной точке и допускаемое касательное напряжение при кручении соответственно.

В случае стержня кругового или кольцевого сечения формулы (3.14), (3.15) принимают следующий вид:

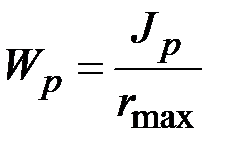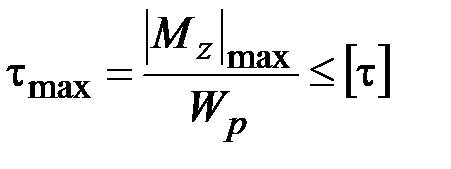, , (3.17)

где 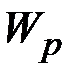– полярный момент инерции сечения, 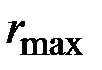– радиус наибольшей окружности кольцевого сечения или радиус круга.

Изгиб стержня в главной плоскости 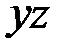. В данном случае по (2.53)

, , .

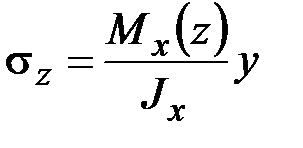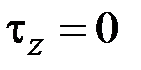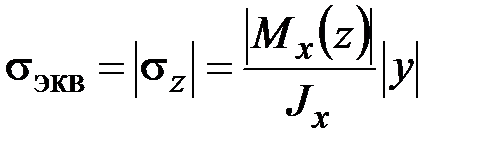Поэтому

,

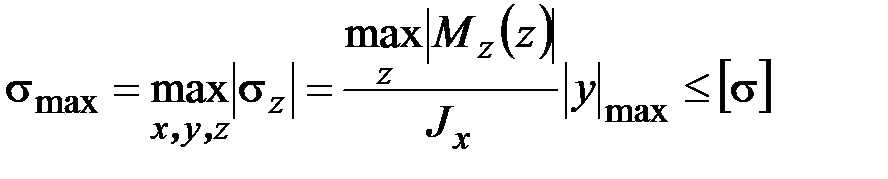где 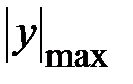– модуль координаты 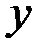наиболее удалённой точки сечения.

Величина

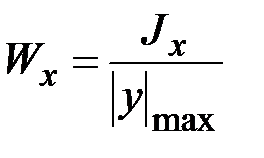(3.18)

называется моментом сопротивления сечения относительно оси .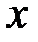
Поэтому

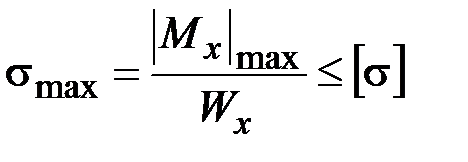. (3.19)

Изгиб стержня в главной плоскости 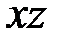. Пользуясь аналогией с предыдущим случаем, можно сразу записать условие прочности

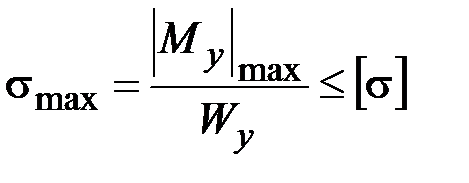, (3.20)

где

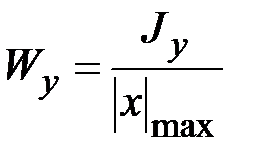(3.21)

– момент сопротивления сечения относительно оси 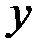, 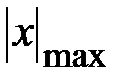– модуль координаты 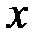наиболее удалённой точки сечения.

Растяжение, изгиб, кручение стержня кругового (кольцевого) сечения. В данном случае по формулам (2.53), (2.54), (3.12)

, , .

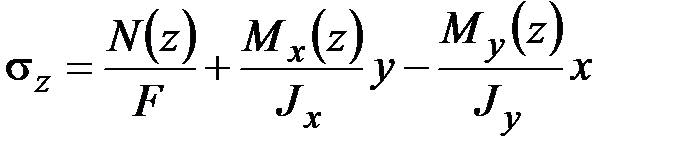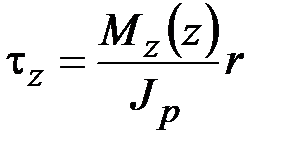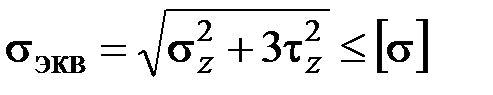Благодаря симметрии сечения данные формулы можно упростить, перейдя к новой системе координат (рис. 3.5, а), относительно которой

, , .

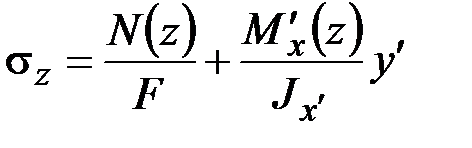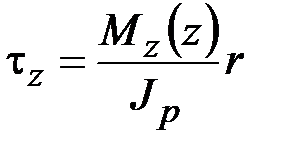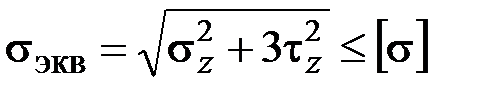Здесь 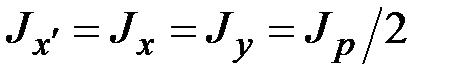, 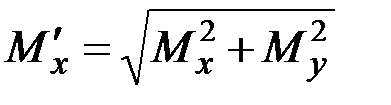– результирующий изгибающий момент. На основании этого можно записать

.

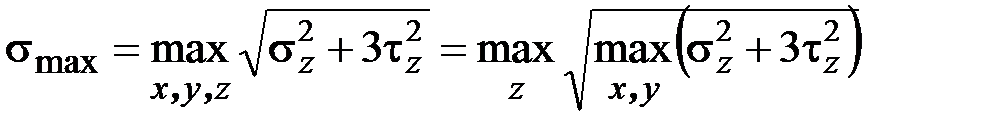б)

а)

Рис. 3.5. К замене системы координат

Нетрудно заметить (рис. 3.5, б), что в поперечном сечении с координатой 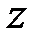опасной является точка 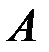, в которой складываются нормальные напряжения от действия продольной силы 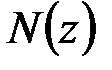и изгибающего момента 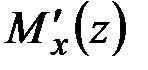. Для данной точки с координатой 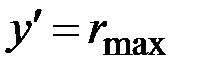с учётом (3.17), (3.18) имеем

.

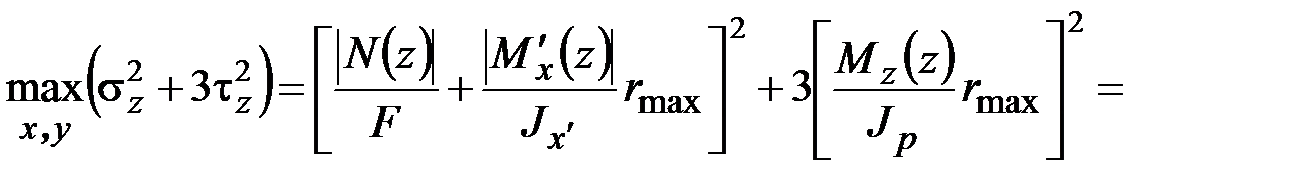
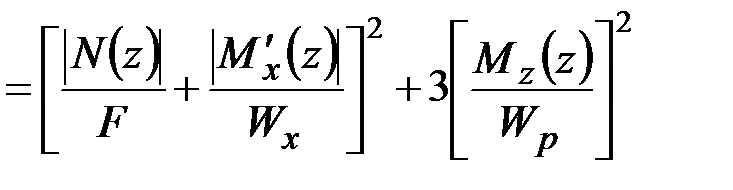Отсюда получаем искомое условие прочности

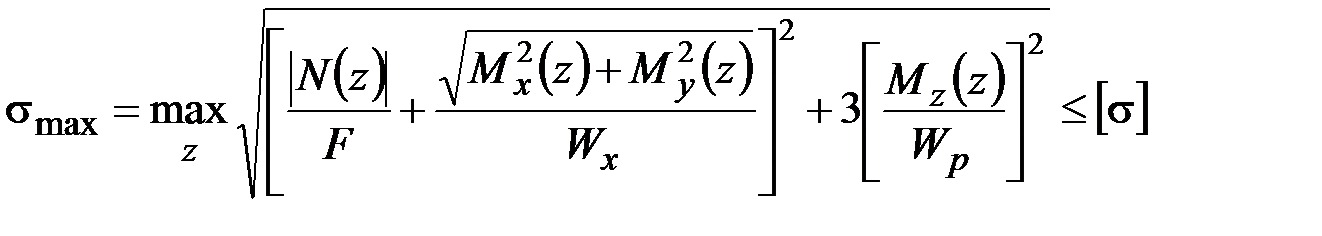. (3.22)

4. Единое представление распределённой
нагрузки и характеристик жёсткости
стержней через обобщённые функции
Дирака и Хевисайда

Рассмотрим одну из типовых схем нагружения прямого стержня распределённой нагрузкой интенсивностью 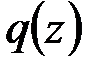и сосредоточенной силой 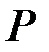, которые для простоты изложения и без ограничения общности положим действующими перпендикулярно оси стержня (рис. 4.1).

Рис. 4.1. Схема нагружения прямого стержня

В данном случае распределение внешних сил по длине стержня описывается функцией погонной нагрузки 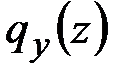, которая складывается из непрерывной функции 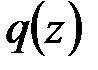и некоторой функции 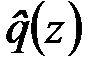, учитывающей действие сосредоточенной силы :

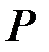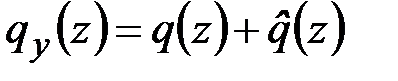. (4.1)

Поскольку сила 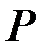приложена в точке 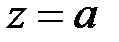, чисто формально имеем

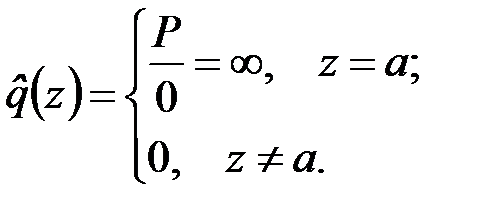(4.2)

В рамках математического анализа функция вида (4.2) не имеет смысла. Чтобы преодолеть эту трудность, можно пойти по простейшему пути и отказаться от использования единого представления распределённой нагрузки (4.1). Однако такой шаг влечёт за собой ряд неудобств из-за необходимости привлечения искусственных приёмов при решении задач сопротивления материалов. Другой, более продуктивный путь состоит в привлечении достаточно простого и наглядного математического аппарата обобщённых функций, который широко применяется в математической физике, квантовой механике и других дисциплинах для описания точечных масс и зарядов, точечных источников теплоты, сосредоточенных сил и моментов.