Обобщённые функции Дирака и Хевисайда

В 1926 г. английский физик Дирак ввёл в квантовой механике символ 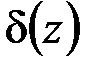, названный им дельта-функцией, которая явилась первой систематически применяемой обобщённой функцией. С физической точки зрения d-функция представлялась Дираком как плотность единичного заряда, помещённого в начале координат. Если этот заряд имеет величину 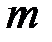, то его линейная плотность (величина заряда на единицу длины)

.

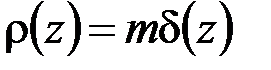Из физических соображений следует, что символ 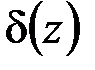обладает свойст­вами

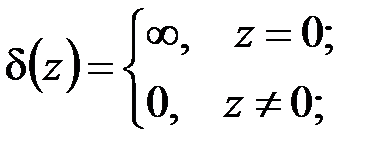
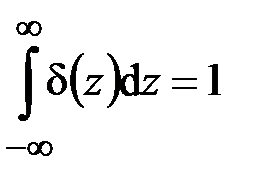. (4.3)

С математической точки зрения символ 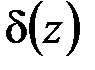со свойствами (4.3) не представляет собой функцию в обычном понимании. В результате сложился некоторый интуитивно ясный формализм в применении d-функции Дирака, с помощью которого физиками достаточно просто были исследованы некоторые важные физические явления. Математикам понадобилось несколько десятков лет, чтобы строго обосновать методы, широко используемые физиками.

Не ставя перед собой задачи полного изложения основ теории обобщённых функций[3], познакомимся с техникой применения обобщённых функций, опираясь на физическое содержание моделируемых явлений.

Дельта-функцию Дирака 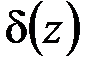можно определить соотношением

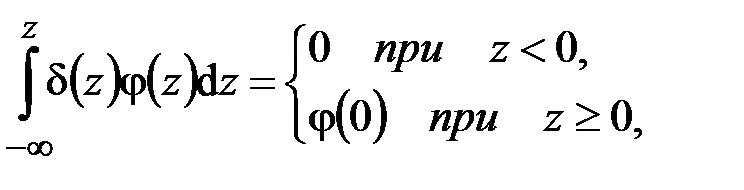(4.4)

где 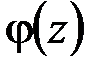– любая непрерывная функция.

Из (4.4) вытекает, что при сдвиге координаты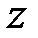

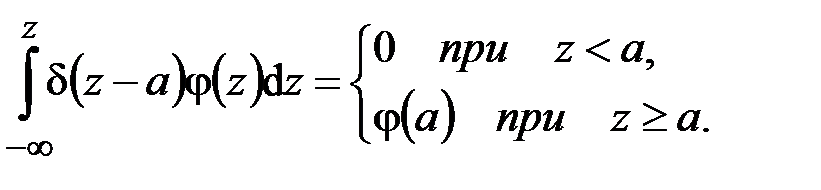(4.5)

Действительно, при замене переменной 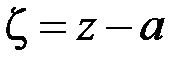из (4.4) будем иметь

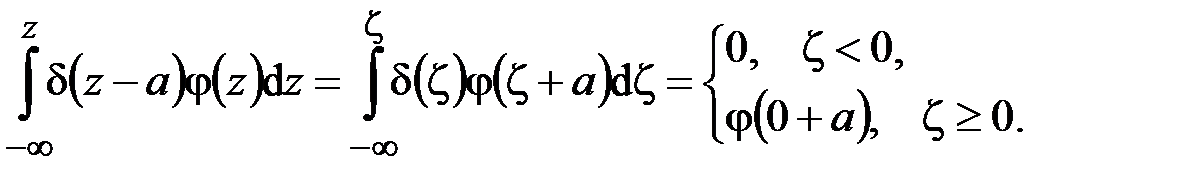
Если в (4.4) положить 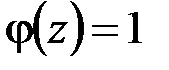, придём к соотношениям

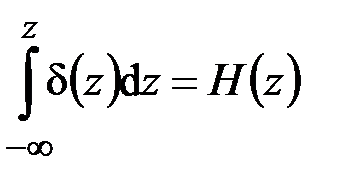Û 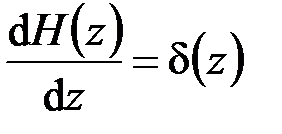, (4.6)

связывающим d-функцию Дирака и так называемую единичную функцию Хевисайда[4] (рис. 4.2, а):

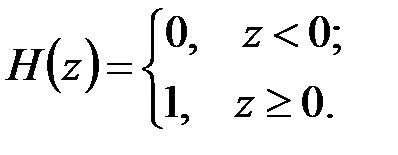(4.7)

Очевидно, что при сдвиге координаты 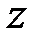на величину 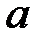(рис. 4.2, в)

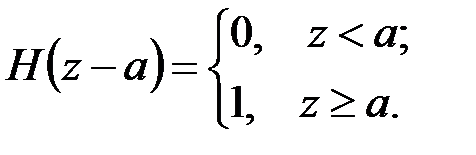(4.8)

Функция Хевисайда обладает следующими интересными свойствами:

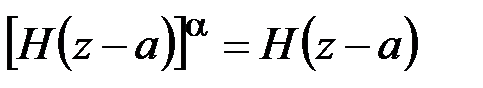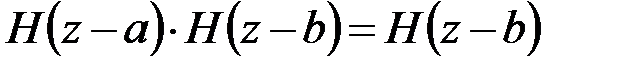, , (4.9)

т. е. при возведении в любую степень 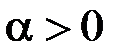функция Хевисайда остаётся неизменной, при перемножении двух функций Хевисайда результат равен тому сомножителю, у которого сдвиг координаты больше: 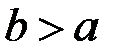. В частности, функция Хевисайда безразмерна. Поэтому, как следует из (4.6), размерность d-функции Дирака обратна размерности аргумента .

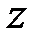Рис. 4.2. Единичная функция Хевисайда

Исходя из (4.7), можно записать (рис. 4.2, б)

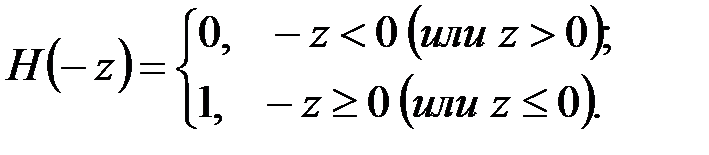
Поэтому

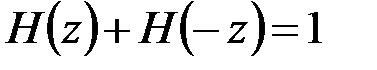. (4.10)

Дифференцируя (4.10) по 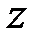и учитывая (4.6), будем иметь

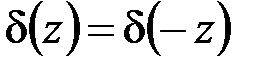. (4.11)

Равенство (4.11) указывает на чётность d-функции Дирака.

Для практических целей чрезвычайно важно, что обобщённую
d-функцию Дирака можно представить как предел последовательности некоторых «хороших» функций, которые называются дельтообразными последовательностями.

Самой простой является последовательность вида (рис. 4.3, а)

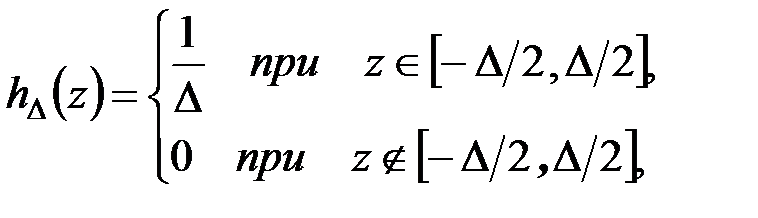
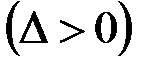. (4.12)

Действительно, для любой непрерывной функци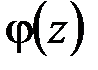и при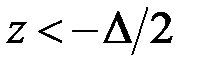

,

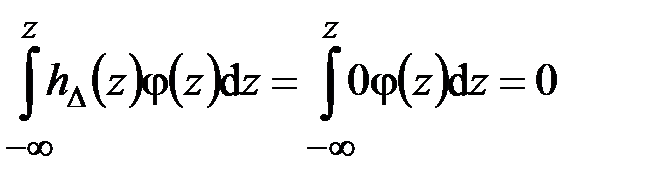а при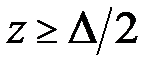

,

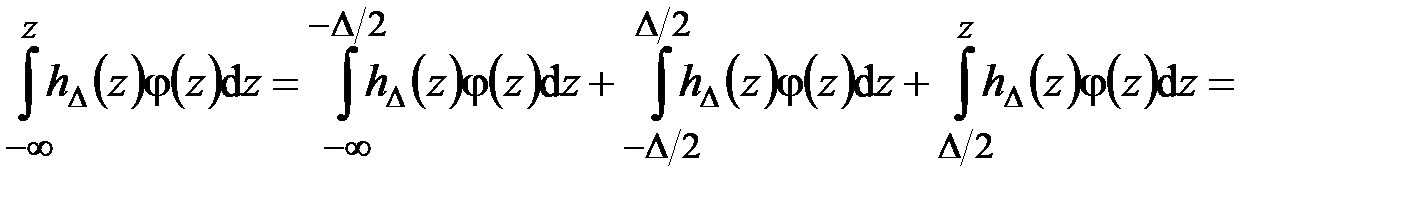
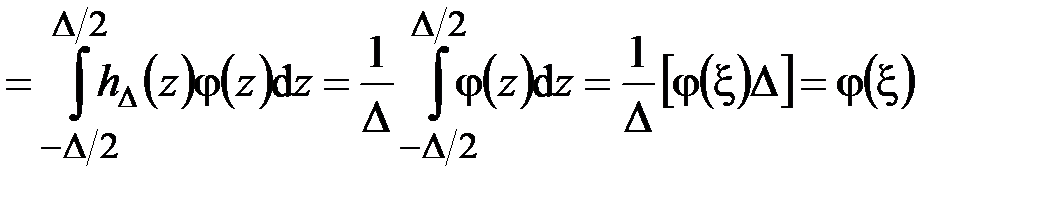где по интегральной теореме о среднем 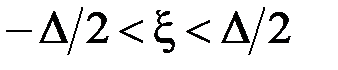. Устремляя теперь положительное число к нулю, приходим к равенству

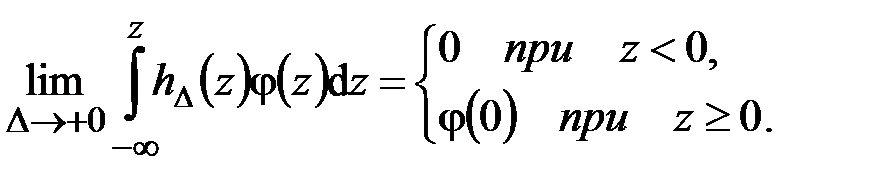
Следовательно,

.

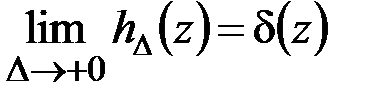Данное предельное равенство обеспечивается благодаря тому, что при любом площадь каждого прямоугольника равна единице (рис. 4.3, а).

Рис. 4.3. Возможные представления d-функции Дирака

Чуть более сложной является последовательность вида (рис. 4.3, б)

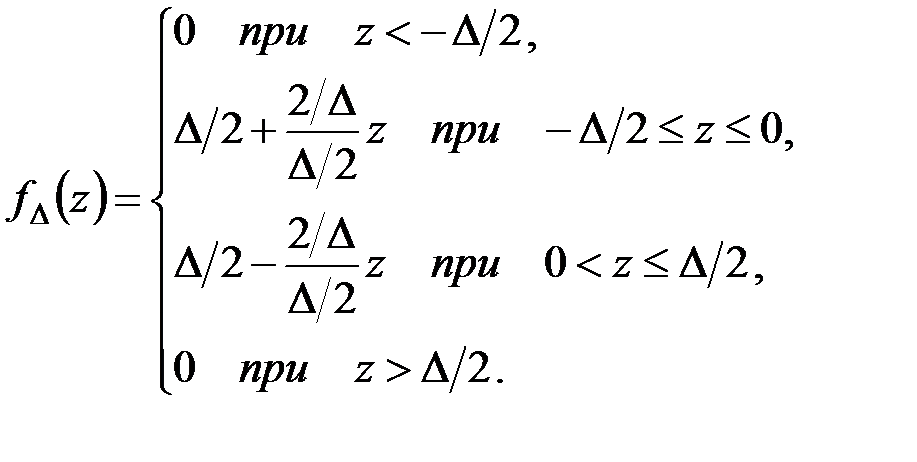(4.13)

Так как площадь каждого треугольника равна единице при любом (рис. 4.3, б), легко убедиться в справедливости равенства

,

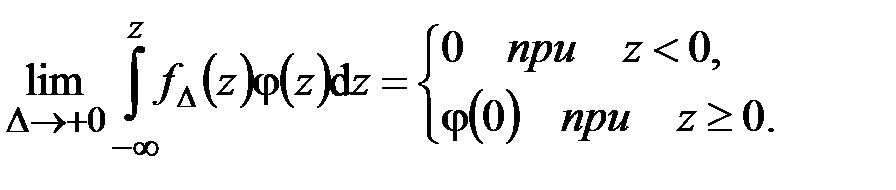
которое означает, что

.

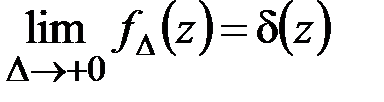Дельтообразных последовательностей, подобных (4.12) и (4.13), существует бесконечно много. Каждую из них можно использовать для представления сосредоточенной силы (или сосредоточенного момента) при проведении численных расчётов на ЭВМ. Делается это следующим простым способом.

Рассмотрим равномерно распределённую на отрезке 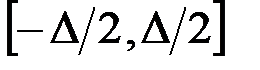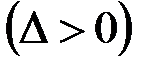погонную нагрузку (рис. 4.4, а)

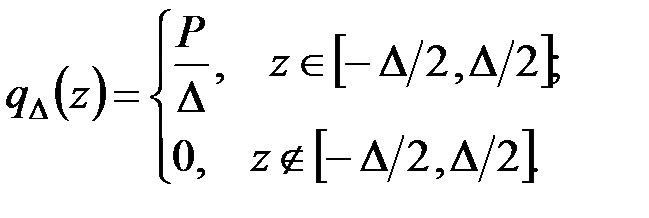(4.14)

Используя дельтообразную последовательность (4.12), распределение (4.14) можно представить в виде

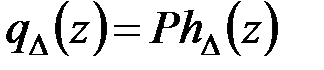. (4.15)

Переходя в (4.15) к пределу 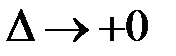, получаем

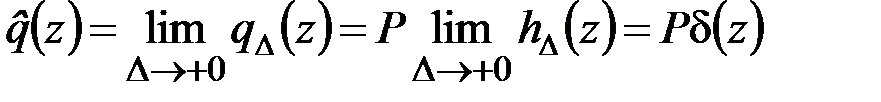. (4.16)

Это и есть математическое представление распределённой нагрузки от действия сосредоточенной силы. В векторной форме (4.16) можно записать так:

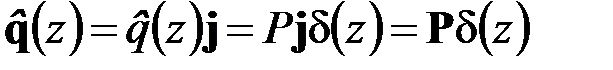, (4.17)

где 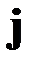– орт оси 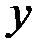. Если сила 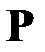приложена не в начале координат, а в другой точке с координатой 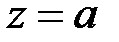(рис. 4.4, б), то тогда соответствующее распределение получается из (4.17) простым сдвигом:

.

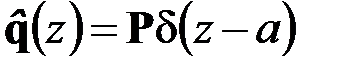Рис. 4.4. Представление сосредоточенной силы
в виде равномерно распределённой нагрузки

Рис. 4.5. Представление сосредоточенной силы
в виде линейно распределённой нагрузки

Заметим, что в (4.15), (4.16) функция 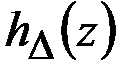играет вспомогательную роль. Вместо неё можно использовать любую другую дельтообразную последовательность, например (4.13). В последнем случае надо рассмотреть нагрузку, распределённую в виде равнобедренного треугольника площадью 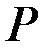(рис. 4.5):

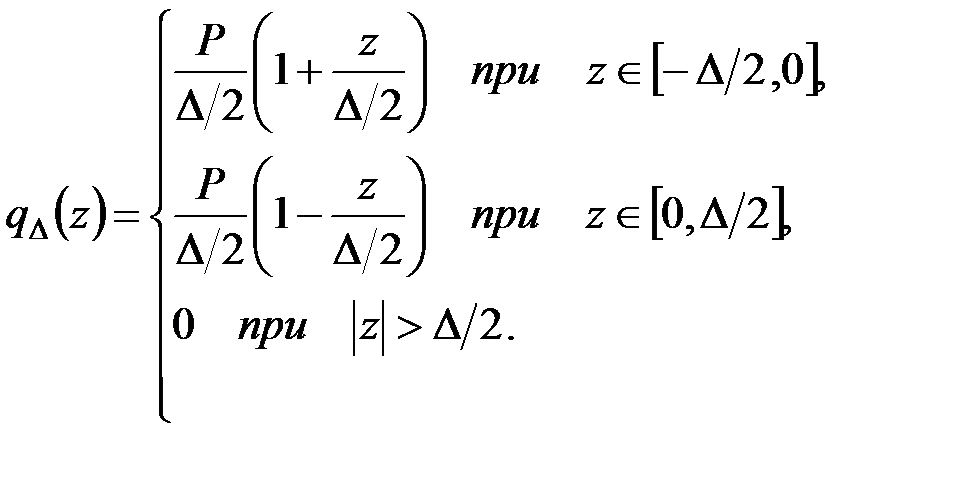
Если переписать (4.13) эквивалентным образом

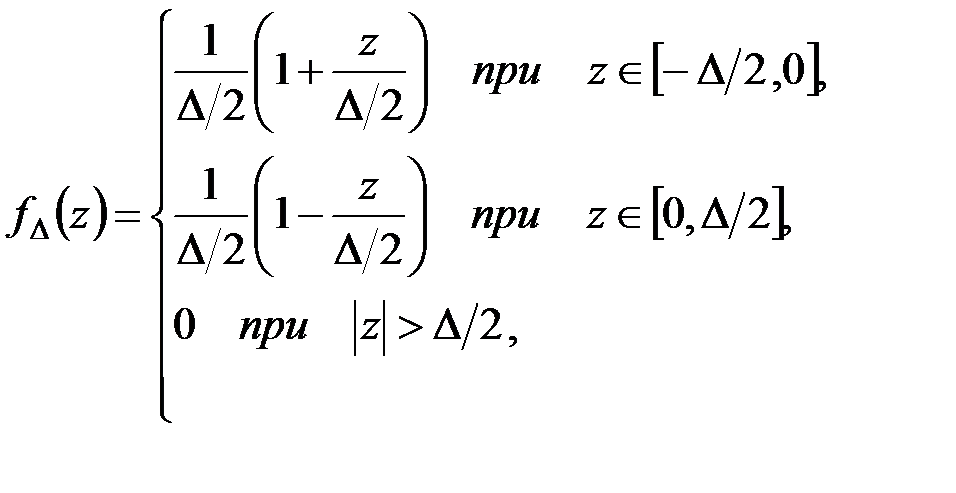
то тогда будем иметь

.

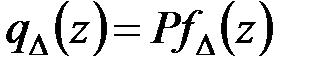Переходя к пределу 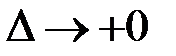, получаем

,

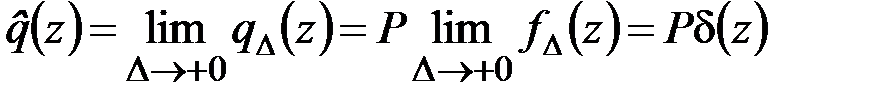что совпадает с представлением (4.16).

Рис. 4.6. К представлению сосредоточенной силы
в виде поверхностной и объёмной распределённой нагрузки

Замечание. До сих пор рассматривалась распределённая нагрузка, приходящаяся на единицу длины. Если сила 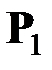приложена в точке 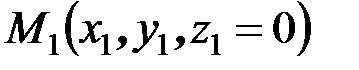на грани параллелепипеда, то она может быть представлена в виде распределённой нагрузки, приходящейся на единицу площади
(рис. 4.6):

.

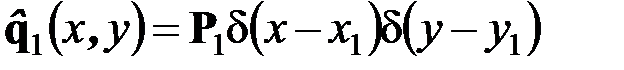Соответственно, сосредоточенная сила 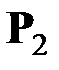, приложенная в некоторой внутренней точке 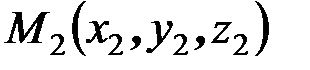параллелепипеда, может быть представлена в виде нагрузки, распределённой по объёму (рис. 4.6):

,

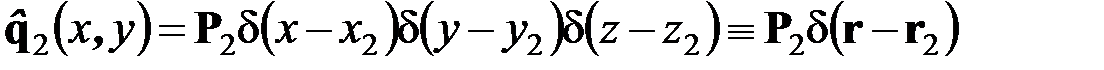где 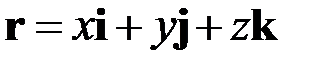– радиус-вектор произвольной точки пространства, 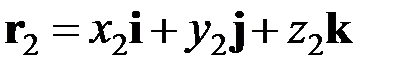– радиус-вектор точки .

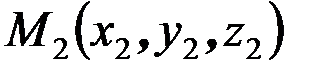4.2. Табличные интегралы
и их практическое применение

При решении задач сопротивления материалов достаточно располагать двумя табличными интегралами, содержащими обобщенные функции Дирака и Хевисайда:

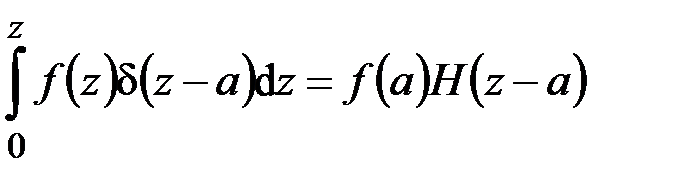, (4.18)

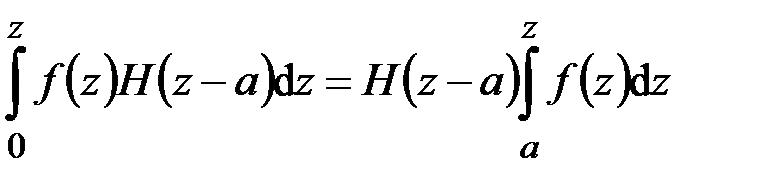, (4.19)

где 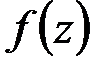– некоторая непрерывная функция, 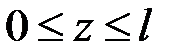, 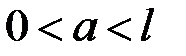. Справедливость (4.18), (4.19) вытекает из (4.5), (4.8):

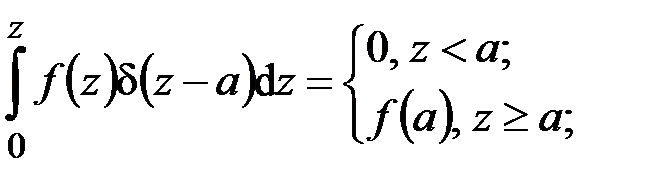
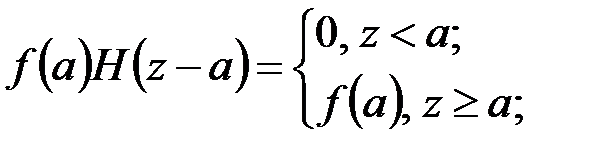
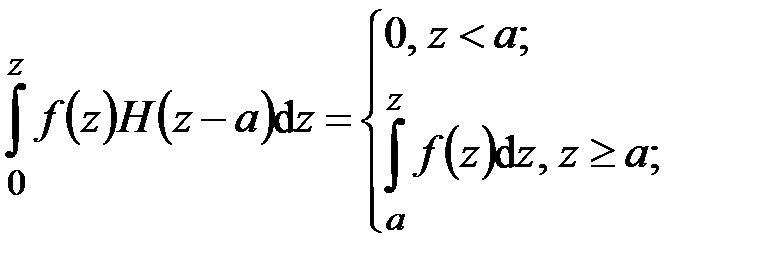
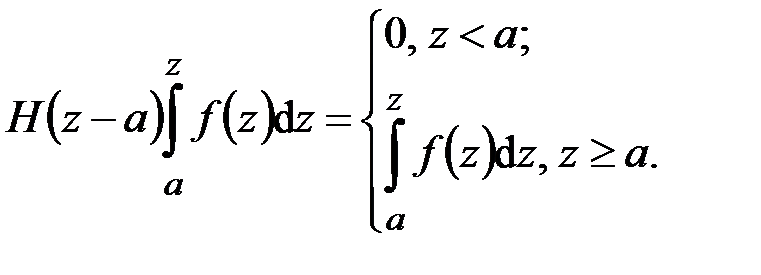
Рис. 4.7. Пример представления активной распределённой нагрузки

Приведём пример вычисления интегралов, содержащих обобщённые функции Дирака и Хевисайда. Глядя на рис. 4.7, а, можно записать

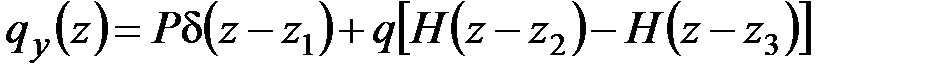
или в развёрнутом виде

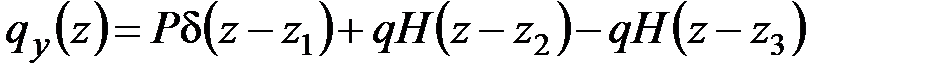. (4.20)

Последние два слагаемых в (4.20) можно интерпретировать как продолжение действия равномерно распределённой нагрузки интенсивностью 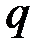до конца стержня и одновременное добавление нагрузки с интенсивностью обратного знака 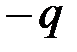, которая, чтобы ничто не изменилось, равномерно распределена на крайне правом участке стержня (рис. 4.7, б).

Вычисляя интеграл от (4.20) с учётом (4.18) и (4.19), получим

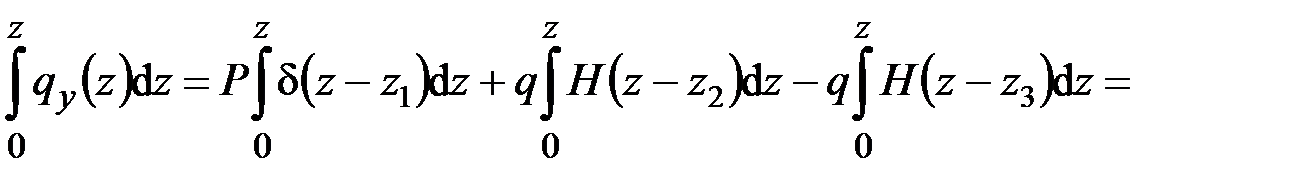
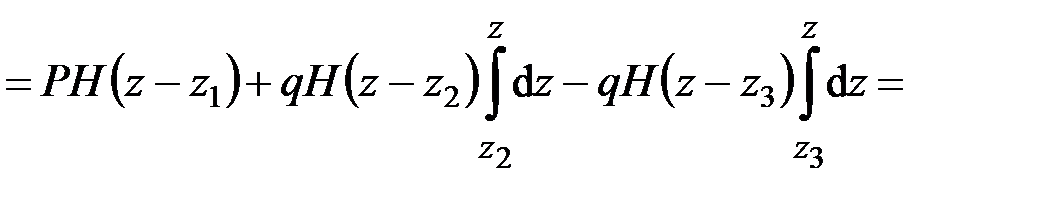
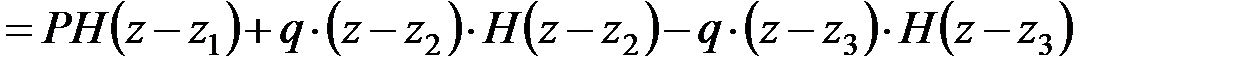
или в развёрнутом виде

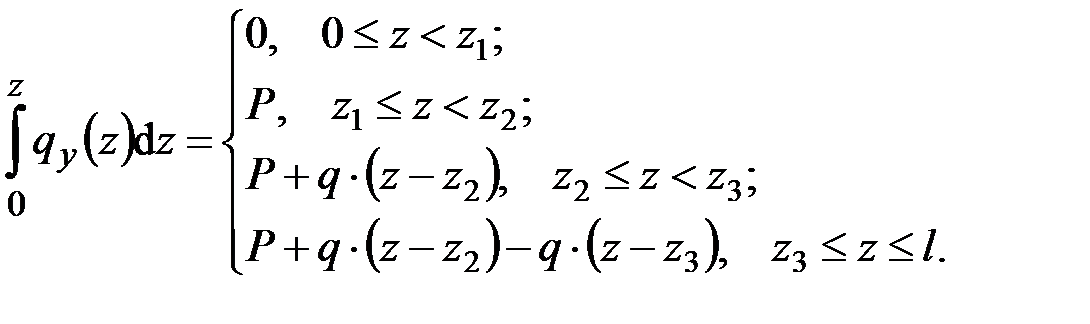
Для полноты общей картины возьмём повторный интеграл:

.

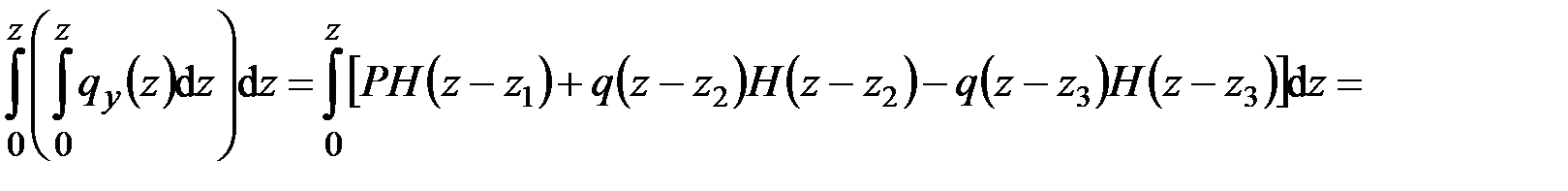
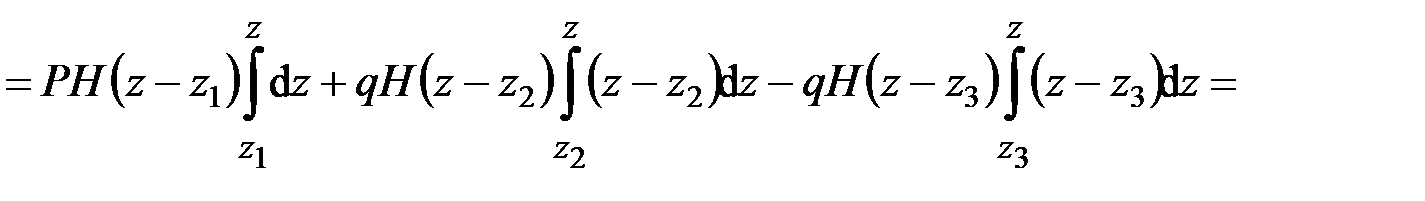
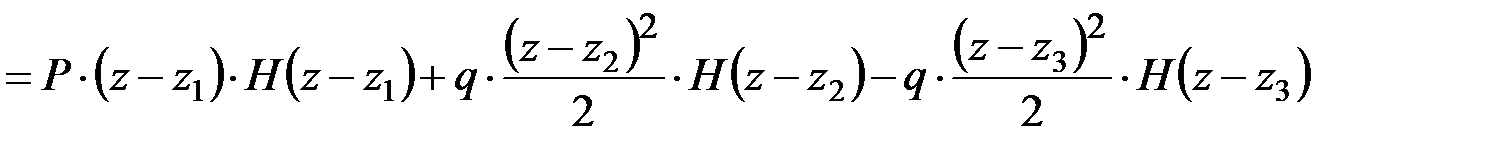В развёрнутом виде данное выражение предстанет так:

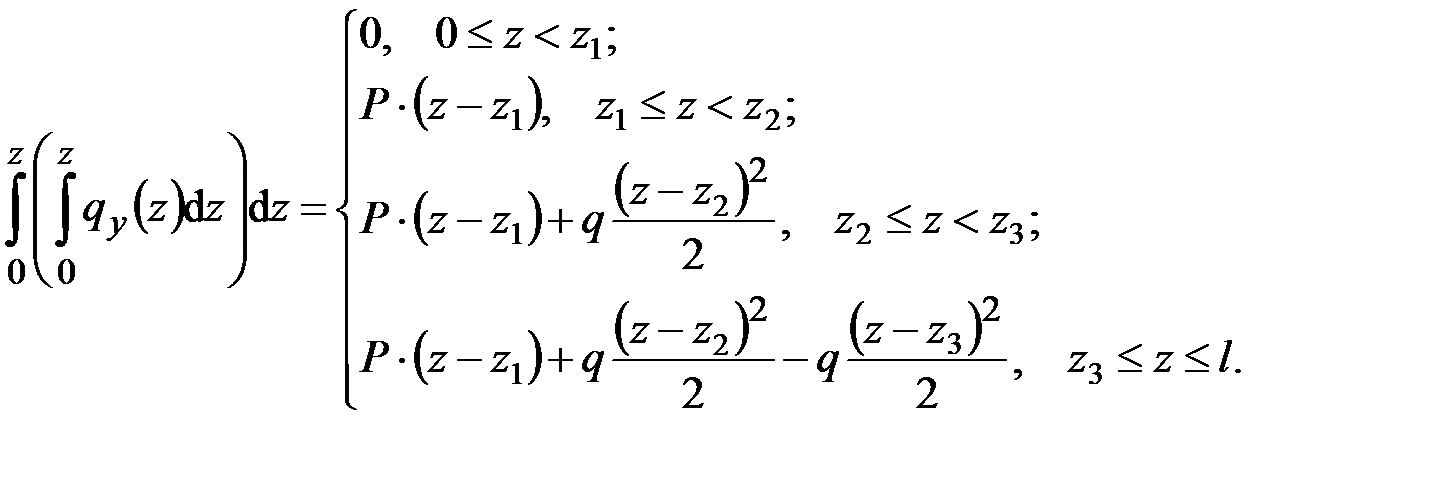
Во всех этих выражениях нетрудно усмотреть простую закономерность.