Гармонический анализ периодических движений.
б) Колебания пилообразной формы
Периодические колебания пилообразной формы, представленные на рис. 111, можно описать функцией 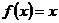 , определяемой в промежутке
, определяемой в промежутке 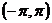 . При других значениях аргумента
. При других значениях аргумента 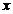 функция повторяется с периодом
функция повторяется с периодом 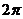 .
.
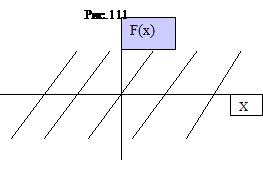 |
Как видно, 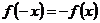 , т.е. функция является нечётной, поэтому из (347) следует, что
, т.е. функция является нечётной, поэтому из (347) следует, что
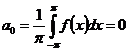 (352).
(352).
Коэффициенты Фурье 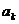 определяется в соответствии с (343)
определяется в соответствии с (343)
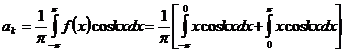 (353).
(353).
Значение интеграла 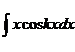 удобно находить по правилу интегрирования по частям. По этому правилу, если подынтегральное выражение можно представить в виде
удобно находить по правилу интегрирования по частям. По этому правилу, если подынтегральное выражение можно представить в виде 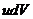 , то с точностью до постоянной интегрирования можно записать:
, то с точностью до постоянной интегрирования можно записать:
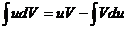 (354).
(354).
Полагая 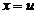 и
и 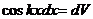 , находим далее, что
, находим далее, что 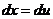 , а
, а 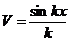 . Используя правило (354) интегрирования по частям, можно записать, что (с точностью до постоянной интегрирования)
. Используя правило (354) интегрирования по частям, можно записать, что (с точностью до постоянной интегрирования)
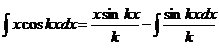 (355).
(355).
Учитывая это, значения коэффициентов 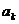 в форме (353) перепишем в виде
в форме (353) перепишем в виде
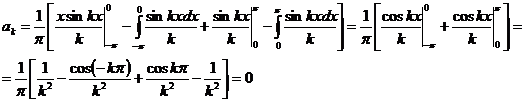 (356).
(356).
Коэффициенты 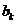 определяются из (354):
определяются из (354):
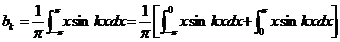 (357).
(357).
Интегралы записанного вида также удобно находить по правилу интегрирования по частям. В этом случае полагаем 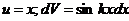 . Учитывая это, получаем далее, что
. Учитывая это, получаем далее, что 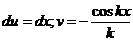 .
.
55.1. Упругие волны.
Рассмотренные в разделе "Колебательное движение" колебательные системы могут служить моделью основной части источника или приёмника упругих колебаний. Теперь обратимся к изучению процесса распространения колебаний, передачи колебательного процесса от источника колебаний к приёмнику.
Изучая колебания различных колебательных систем, мы, как правило, не учитываем тех изменений, которые колебательная система производит в окружающей её среде. Между тем, колеблющееся тело, отклоняясь от положения равновесия, вызывает деформации окружающего его участка среды и, соответственно, упругие напряжения. Силы упругости в деформированном участке среды действуют как на колеблющееся тело, так и на частицы слоев среды, граничащих с деформированным. Под действием упругих сил частицы совершают движение в соответствии с законами динамики. Таким образом колебательный процесс, возбуждаемый колеблющимся телом, начинает распространяться в среде. При периодических колебаниях источника периодическими будут и колебания различных частиц среды около их положений равновесия. С течением времени в колебательный процесс вовлекаются всё более и более удалённые от источника частицы среды. Такой процесс и называют обычно волновым, а изменяющиеся с течением времени периодические деформации среды - волной. Более того, даже если источник возмущений в среде является импульсным, а не периодическим, процесс распространения возмущений в среде всё равно называют волновым. Следовательно, для распространения колебаний, возбуждаемых источником, необходимо наличие упругой среды. Здесь и далее рассматриваются только упругие волны, хотя волновым процессом можно описывать и изменения в пространстве с течением времени и других по природе физических величин, например, температуры (для температурных или тепловых волн), напряженности электрического поля для электромагнитных волн и т.д.
