Тема: исследование функции с помощью производной

Цель: научиться исследовать свойства функции и строить её график с помощью

производной.

Оснащение занятия: учебник, конспект, справочник.

Порядок выполнения работы

Задание 1. Организуйте работу парами и дайте (устно) ответы на вопросы:

1. Что называется, областью определения функции?

2. Характеризуется ли возрастание и убывание функции знаком её производной? Если да, то сформулируйте правило возрастания и убывания функции.

3. Какие точки называют стационарными?

4. Какие точки называют точками экстремума? Как называют значения функции в точках экстремума?

По окончании работы в парах ответы будут заслушаны перед группой.

Задание 2. Выполните №923.

Задание 3. Повторите схему исследования свойств функции (п.51, стр.268).

Задание 4. Рассмотрите решение задачи 1, стр.267, затем по схеме исследования свойств функции постройте график данной функции самостоятельно. Сравните результаты.

Задание 5. Постройте график функции

Задание 6. Рассмотрите решение задачи 3, стр.269 и запишите вывод.

Задание 7. Выполните №927(1,3).

Задание 8. Рассмотрите решение задачи 4, стр.271. Полное её решение запишите самостоятельно.

Задание 9. Постройте график функции:

В-1. №926(1), №928(2), № 930(3), № 932(1).

В-2. №926(3), №928(1), №930(2), №932(2).

Литература: Алимов Ш. А. Алгебра и начала анализа стр.267.

Практическая работа № 33

Тема: Первообразная

Цели:

– научиться находить первообразные заданных функций;

– закрепить теоретические знания по теме «Производная».

Оснащение занятия: учебники, справочники, конспекты, таблица первообразных.

Порядок выполнения работы

Задание 1. Повторение теоретического материала.

1.Что следует понимать под дифференцированием функции? Устно №802.

2.Что называется первообразной функции? Выполните устно №983.

Задание 2. Рассмотрите решение задачи 2 стр.289 и составьте план нахождения первообразной для заданной функции, график которой проходит через некоторую точку. Ответ будет заслушан перед группой.

Задание 3. Выполните №1033(1) в парах. В-1. №1033(3). В-2. №1033(5).

Задание 4. Повторите таблицу первообразных на стр.290. Организуйте работу парами и проверьте друг друга.

Задание 5. Рассмотрите решение задачи 1, стр.291 и выполните №988(3), №989(5;7), №990(3).

В-1. №988(1), №989(1), №990(5). В-2. №988(5), №989(3), №990(1).

Задание 6. Рассмотрите решение задачи 2, стр.291 и выполните №991(5;7).

В-1. №991(1), №992(3). В-2. №991(3), №992(1).

Задание 7. В группе выполните №993(2;4), №994(2;4)–№998(2;4).

В-1. №993(3), №994(1), №995(1). В-2. №993(1), №994(3),№995(3).

Литература: Алимов Ш. А. Алгебра и начала анализа стр.287-290.

Практическая работа № 34

Тема: Вычисление площадей плоских фигур

Цель: научиться находить площадь фигуры, ограниченной заданными линиями.

Оснащение занятия: учебники, конспекты, плакаты.

Порядок выполнения работы

Задание 1. Повторение учебного материала.

1. Сформулируйте определение криволинейной трапецией?

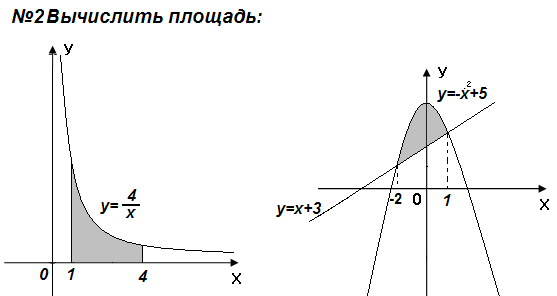
2. Запишите формулы для вычисления площади фигур, заштрихованных на рисунке.

Задание 2. Выполните в парах № 1015(2), № 1039(4).

Задание 3. Выполните самостоятельно.

Вариант 1. № 1014 (1), № 1016(1), № 1038(1), № 1017(2).

Вариант 2. № 1014 (3), № 1016(2), № 1038(2), № 1017(1).

Литература: Алимов Ш. А. Алгебра и начала анализа стр. 293, стр. 300.

Практическая работа № 35

Тема:Комбинаторика

Комбинаторными задачами называются задачи, в которых необходимо подсчитать, сколькими способами можно сделать тот или иной выбор, выполнить какое-либо условие.

Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k элементов:

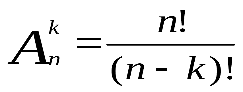, где n!=1*2*3*…*n

Пример.Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных урока?

Решение.Число способов равно числу размещений из 7 элементов по 4, т.е. равно 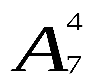. Получаем = .

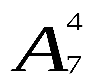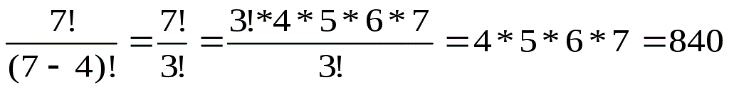Размещения из nэлементов поnэлементов называютсяперестановками из n элементов:

.

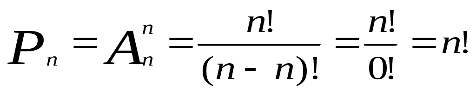Пример.Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?

Решение.Цифра 5 обязана стоять на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е. 5!=5*4*3*2*1=120.

Сочетания.Пусть имеется множество, состоящее изnэлементов. Каждое его подмножество, содержащееkэлементов, называетсясочетанием из nэлементов по k элементов:

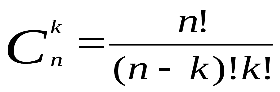
Пример.Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?

Решение.Матчей состоится столько, сколько существует двухэлементных подмножеств у множества, состоящего из 16 элементов, т.е. их число равно .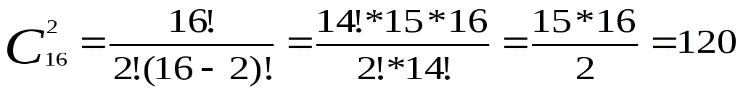

Свойства сочетаний:

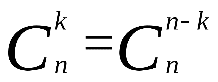
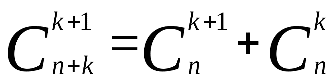
Задача № 1. Сколькими способами могут быть расставлены 5 участниц финальногозабега на 5-ти беговых дорожках?

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждаяцифра входит в изображение числа только один раз?

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шестидевушек на танец?

Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,6, 7, 8, 9 при условии, что в записи числа каждая цифра используется толькоодин раз?

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3человек?

Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантовраспределения призовых (1, 2, 3) мест?

Практическая работа № 36