Раскрытие неопределенности по правилу Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида  или
или  , то
, то 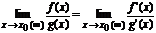 .
.
Доказательство. Рассмотрим доказательство теоремы для неопределенности вида  при
при 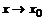 .
.
Для простоты будем предполагать, что функции 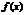 и
и 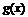 , а также их производные непрерывны в точке
, а также их производные непрерывны в точке 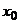 , причем
, причем 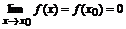 и
и 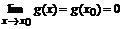 . В этом случае
. В этом случае 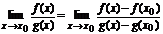 .
.
Применяя теорему Лагранжа для функций 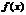 и
и 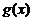 на отрезке
на отрезке 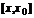 , получим
, получим 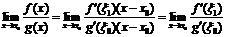 , где
, где 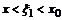 ,
, 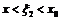 .
.
При 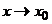 в силу непрерывности производных
в силу непрерывности производных 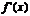 и
и 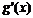 имеем
имеем 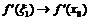 и
и 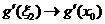 . Используя теорему о пределе частного получаем равенство
. Используя теорему о пределе частного получаем равенство 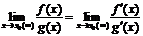 .
.
Пример. Раскрыть неопределенность по правилу Лопиталя и найти предел функции: 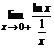 .
.
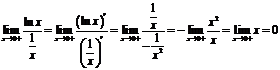 .
.
44.Правила исследования функций.
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Исследовать функцию 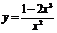 и построить ее график.
и построить ее график.
1. Область определения функции.
Область определения функции 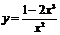 :
: 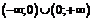 .
.
2. Исследование функции на четность-нечетность.
Так как 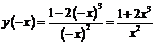 , то функция
, то функция 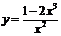 общего вида.
общего вида.
3. Исследование функции на наличие вертикальных асимптот.
Прямая 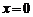 является вертикальной асимптотой, так как
является вертикальной асимптотой, так как 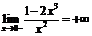 ,
, 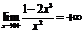 .
.
4. Исследование поведение функции в бесконечности, нахождение горизонтальных и наклонных асимптот.
Так как 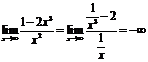 , то функция горизонтальных асимптот не имеет.
, то функция горизонтальных асимптот не имеет.
Так как 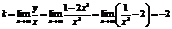 ,
, 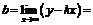
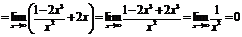 , то прямая
, то прямая 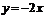 является наклонной асимптотой.
является наклонной асимптотой.
5. Экстремумы и интервалы монотонности функции.
Найдем производную первого порядка 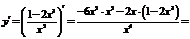
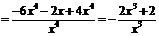 . Приравняем первую производную к нулю
. Приравняем первую производную к нулю 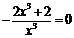 , откуда
, откуда 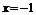 ,
, 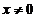 . Знаки производной первого порядка указаны на рисунке.
. Знаки производной первого порядка указаны на рисунке.
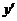 | - | + | - | |
 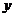 | -1 | 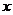 |
Функция возрастает на интервале 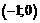 , убывает -
, убывает - 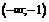 ,
, 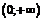 . Точка
. Точка 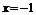 является точкой минимума
является точкой минимума 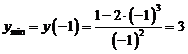 .
.
6. Определим интервалы выпуклости функции и точки перегиба.
Найдем производную второго порядка 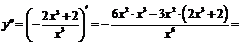
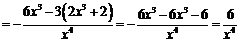 . Приравняем вторую производную к нулю
. Приравняем вторую производную к нулю 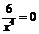 , откуда
, откуда 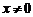 . Знаки производной второго порядка указаны на рисунке.
. Знаки производной второго порядка указаны на рисунке.
 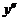 | + | + | |
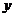 | 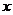 |
Функция выпукла вверх на интервалах 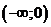 ,
, 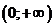 . Точек перегиба нет.
. Точек перегиба нет.
7. Точки пересечения с осями координат.
Точка 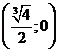 является точкой пересечения функции с осью абсцисс.
является точкой пересечения функции с осью абсцисс.
ВОПРОС 45. Функции нескольких переменных. Поверхности и линии уровня, поверхности и кривые безразличия.
Функции нескольких переменных. Определение. Если каждой паре (x,y) значений двух независимых переменных из области W ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y). z=f(x,y)
Геометрическое изображение функции двух переменных - поверхность.
Частное и полное приращение функции.
Полное приращение функции Dz=f(x+Dx, y+Dy)-f(x,y)
Частное приращение функции Dx z=f(x+Dx)-f(x,y)
Поверхности и линии уровня
Поверхностью уровня поля 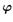 называют геометрическое место точек, в которых поле принимает постоянное значение. Согласно такому определению, уравнение поверхности уровня будет иметь вид:
называют геометрическое место точек, в которых поле принимает постоянное значение. Согласно такому определению, уравнение поверхности уровня будет иметь вид: 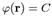 или
или 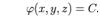
Кривые безразличия — представляют собой совокупность точек на координатной плоскости, каждая из которых является потребительским набором, обеспечивающим потребителю одинаковый уровень удовлетворения его потребностей. Кривая безразличия является графическим отображением набора безразличия
