Предел функции. Непрерывность в точке, на интервале. Свойства.

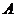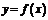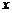Определение. Число называется пределом функции при , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 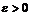, найдется такое положительное число 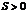(зависящее от 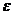; 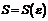), что для всех 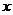таких, что 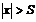, верно неравенство: .

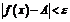Определение. Число 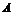называется пределом функци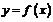и при 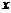, стремящемся к 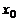(или в точке 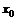), если для любого, даже сколь угодно малого положительного числа 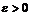, найдется такое положительное число 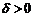(зависящее от 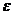; 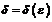), что для всех 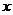, не равных 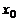и удовлетворяющих условию 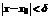, выполняется неравенство: .

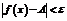Теоремы о пределах:

Функция не может иметь более одного предела.

1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. .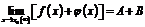

2. Предел произведений конечного числа функций равен произведению пределов этих функций, т.е. .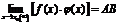

3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е. .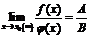

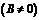4. Если 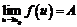, , 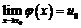то предел сложной функции .

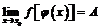5. Если в некоторой окрестности точки 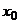(или при достаточно больших 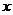) 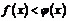, то .

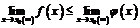Пример. Вычислить .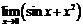

.

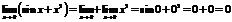Определение. Функция 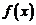называется непрерывной в точке 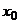, если она удовлетворяет следующим трем условиям: 1) определена в точке 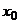(т.е. существует 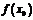); 2) имеет конечный предел функции при 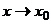; 3) этот предел равен значению функции в точке 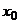, т.е. .

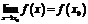Свойства функций, непрерывных в точке:

1. Если функция 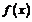и 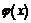непрерывны в точке 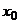, то их сумма 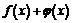, произведение 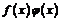и частное 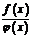(при условии 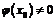) являются функциями, непрерывными в точке .

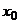2. Если функция 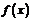непрерывны в точке 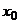и 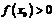, то существует такая окрестность точки 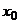, в которой .

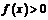3. Если функция 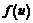непрерывны в точке 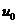, а функция 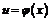непрерывны в точке 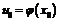, то сложная функция 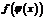непрерывна в точке .

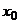Пример. Функция 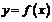задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.

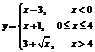
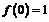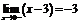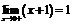Так как , и , , т.е. 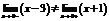, то в точке 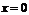функция 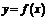не является непрерывной.

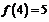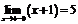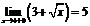Так как , и , , т.е. 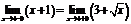, то в точке 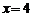функция 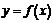непрерывна.

30 вопрос тоже.

Определение. Функция 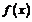называется непрерывной на промежутке 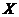, если она непрерывна в каждой точке этого промежутка.

Свойства функций, непрерывных на отрезке:

1. Если функция 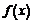непрерывна на отрезке 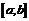, то она ограниченна на этом отрезке.

2. Если функция 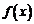непрерывна на отрезке 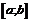, то она достигает на этом отрезке наименьшего значения 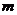и наибольшего значения .

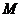3. Если функция 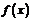непрерывна на отрезке 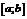и значение ее на концах отрезка 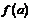и 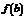имеют противоположные знаки, то внутри отрезка найдется точка 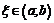такая, что .

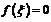Пример. Доказать непрерывность функции .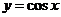

Найдем 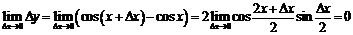. Так как 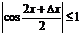, а 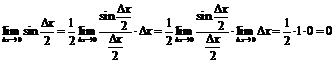, т.е. 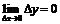, то функция 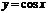является непрерывной на всей числовой оси.

ВОПРОС 27. . Основные теоремы о пределах.

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.

lim_{x a}=

1. Функция ограниченная при x a.
2. Функция ограниченная при x .
3. Теорема. Если lim_{x a} f(x)=b, то функция f(x) ограниченная при x a.
4. Бесконечно малые и их свойства. lim_{x a} (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_{x a} f(x)=b и обратно, если lim_{x a}f(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_{x a} (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

1. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_{x a} u(x)=lim_{x a} v(x)=b, то lim_{x a} z(x)=b. ("Теорема о двух милиционерах").

0.5sin(x) < 0.5x < 0.5tg(x)

1. Первый замечательный предел.

lim x® 0

sin(x) x

=1.

1. Второй замечательный предел.

Переменная величина

æ è 1+ n ö ø n

при n® ¥ имеет предел, заключенный между 2 и 3.

ВОПРОС 32.Бесконечно малые величины, основные теоремы о бесконечно малых.

ВОПРОС 33. Бесконечно большие величины, связь бесконечно малых с бесконечными величинами.

ВОПРОС 36. .Дифференцируемость функции, первый дифференциал и производная первого порядка.. Связь непрерывности и дифференцируемости

Пусть функция задана в некоторой области , и -- внутренняя точка этой области. Пусть -- произвольная точка этой же области . Разность называется приращением аргумента ; , где . Разность значений функции называется приращением, или полным приращением функции в точке , соответствующим приращению аргумента ; -- это функция от точки и приращения .

Предположим, что приращение функции можно представить в виде

(7.2

где -- некоторые числа. Подчеркнём, что эти числа не зависят от , но могут измениться, если сменить точку . Относительно величины мы предположим, что это функция, при базе являющаяся величиной большего порядка малости, чем . Это означает, если вспомнить определение бесконечно малой величины большего порядка малости относительно другой бесконечно малой, что

Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, -- это линейная функция от приращения аргумента , если точка фиксирована. Условие большей малости последнего слагаемого (7.2) относительно означает, что эта линейная функция -- главная часть приращения функции.

Определение 7.11 Если указанное представление (7.2) имеет место, то функцию называют дифференцируемой в точке , а линейную относительно функцию

то есть главную линейную часть приращения функции, -- дифференциалом функции в точке .

Если функция является дифференцируемой в любой точке открытой области , то функцию называют дифференцируемой в области .

Таким образом, приращение дифференцируемой функции можно представить в виде суммы дифференциала , то есть линейной части приращения, и остатка , который имеет более высокий порядок малости, чем приращение :

Теорема 7.8 Дифференцируемая в точке функция является непрерывной в этой точке.

Доказательство. Действительно, если , то стремятся к 0 все слагаемые дифференциала: они имеют вид ; множитель не зависит от , то есть постоянен, а , поскольку Величина также стремится к 0, так как имеет даже больший порядок малости, чем . Значит, . Но условие как раз и означает, что при , то есть что функция непрерывна в точке .

ВОПРОС 37. Правила дифференцирования. Таблица производных.

ВОПРОС 39.Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля).

ТеоремаФерма

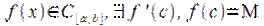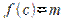Пусть функция или в т.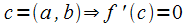

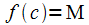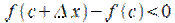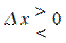Пусть, для определённости, (рис. 10.1), тогда при и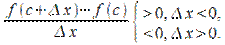

Согласно определению производной имеем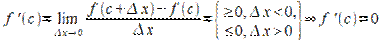

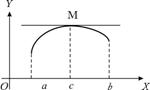
Рис. 10.1

Геометрическоеистолкованиетеоремывытекаетизгеометрическогосмыслапроизводной: касательная к графику функции 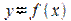в точке с абсциссой 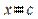параллельна оси .

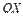Теорема Ролля

Пусть функция 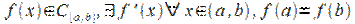. Тогда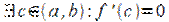

Из условия 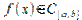следуетпосвойству10непрерывныхна 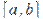функций, что .

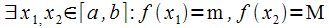Существует две возможности:

1) ;

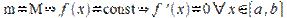2) 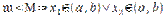в силу .

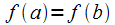Пусть 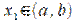, тогда согласно теореме Ферма .

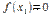Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.

ВОПРОС 40. Теорема Лагранжа (формула конечных приращений). Связь теоремы Коши с теоремой Лагранжа.

Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция 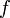непрерывна на отрезке 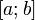и дифференцируема в интервале 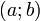, то найдётся такая точка 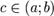, что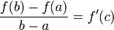

Геометрически это можно переформулировать так: на отрезке 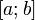найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Вопрос 41.Теорема Коши́

Теорема Коши о среднем значении является обобщением теоремы Лагранжа о конечных приращениях

Пусть на отрезке определены две непрерывные фунции 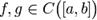. Пусть также 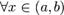существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть 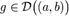, и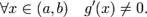

Тогда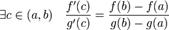

Пример. Проверить, что функци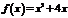и и 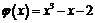на отрезке 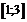удовлетворяют условиям Коши.

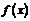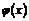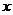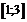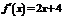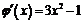Функции и непрерывны при всех , а значит, и на отрезке ; их производные и существуют везде; кроме того, 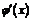на заданном отрезке не обращается в нуль.

Следовательно, к данным функциям применима теорема Коши: 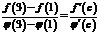, т.е. 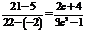, откуда находим два значения : , .

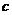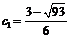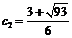Из полученных значений только 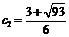удовлетворяет условию задачи, так как 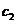является внутренней точкой отрезка .

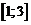Вопрос 43. Формула Тейлора

Формула Тейлора. Пусть функция 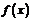имеет в точке 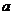и некоторой ее окрестности производные порядка 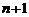. Пусть 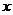- любое значение аргумента из указанной окрестности, 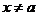. Тогда между точкам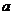и и 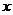найдется точка 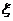така, что справедлива формула Тейлора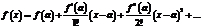 .
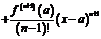