Числовые ряды. Основные теоремы о сходимости

Числовой ряд – это сумма членов числовой последовательности вида .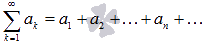

Необходимый признак сходимости числового ряда:
Если ряд 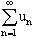сходится, то .

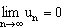Данный признак означает, что если 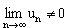, то ряд расходится. Например, 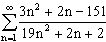расходится, так как 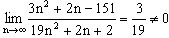. Из выполнения условия 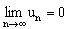в общем случае не следует сходимость ряда 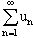. Например, для ряда 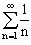(гармонический ряд), условие 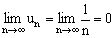выполнено, но данный ряд расходится.

Положительные числовые ряды. Признаки Коши и Даламбера

Положительные ряды

Если a_n ≥ 0 (n = 1, 2, 3, ... ), то ряд a₁ + a₂ + a₃ + ... называется положительным. В том случае, когда при всех n оказывается a_n > 0, будем называть ряд строго положительным.

Положительные ряды обладают многими свойствами, сближающими их с обычными суммами конечного числа слагаемых.

Легко видеть, что частичная сумма

S_n = a₁ + a₂ + ... + a_n

положительного ряда возрастает (может быть, не строго) с увеличением n. Так как всякая возрастающая числовая последовательность имеет конечный или бесконечный предел (причем члены последовательности не превосходят этого предела), то для любого положительного ряда существует предел

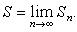
Этот предел будет конечным или бесконечным, смотря по тому, ограничено сверху или нет множество частичных сумм {S_n}

Теорема (признак Даламбера). Пусть для числового ряда с положительными членами:

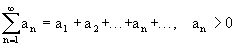
cуществует 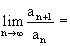l, то

при l<1 ряд сходится,

при l>1 ряд расходится,

при l=1 ряд может сходиться или расходиться (в этом случае признак на вопрос о сходимости ряда ответа не дает).

По определнию предела > 0 N=N( ), что n>N выполняется неравенство:

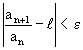или .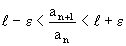

Выберем N так, чтобы для n>N было l+ =q<1, тогда

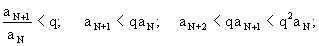
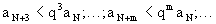
Ряд a_Nq+a_Nq²+...+a_Nq^m+... сходится, так как знаменатель прогрессии q<1. Тогда по теореме 1 ряд 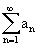также сходится.

Для случая q>1 доказательство аналогично, только нужно рассмотреть .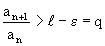

Признак Коши:Если существует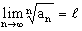, то при l<1 ряд сходится; l>1 - ряд расходится; l=1 — определить сходимость невозможно.

Доказательство признака Коши аналогично доказательству признака Даламбера.

Знакочередующиеся числовые ряды. Абсолютная и условная сходимости

Знакочередующимся числовым рядом называется ряд

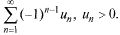
Абсолютная и условная сходимость

Ряд 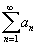называется абсолютно сходящимся, если ряд 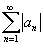также сходится.
Если ряд 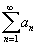сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд 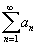называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Функциональные ряды. Равномерная сходимость функционального ряда.

Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция .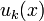

Равномерная сходимость

Существует функция 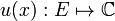такая, что: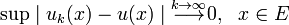

Факт равномерной сходимости последовательности 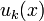к функции 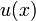записывается: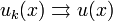

Степенные ряды

Определение

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

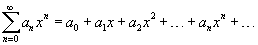
Часто рассматривается также ряд, расположенный по степеням (x − x₀), то есть ряд вида

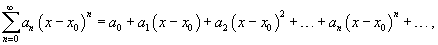
где x₀ − действительное число.