Интегрирование тригонометрических уравнений

1)Интегрирование дифференциалов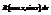

В любом промежутке вида 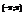для интегрирования указанных дифференциалов можно применить универсальную подстановку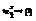

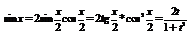
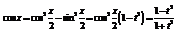
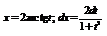
Таким образом, интеграл 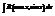всегда выражается в конечном виде. Для их выражения кроме функций встречающихся при интегрировании рациональных выражений нужны лишь тригонометрические функции.

2)Универсальная подстановка всегда ведет к цели, но в силу своей общности, она часто не является лучшей в плане краткости.

Рассмотрим частные случаи:

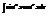, данный интеграл находится с помощью тригонометрических формул в зависимости от n и m.

а)Если хотя бы одно из n и m положительно и нечетно, то от нечетной степени отделяем множитель, а оставшийся, в четной степени, преобразуем через , отделенный множитель вместе с dx дают либо дифференциал синуса, либо косинуса.

б) Если n и m оба положительные и четные, то применяем формулы понижения порядка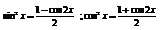

в) Если выгодно выполнить

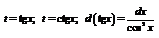
4. Интегрирование иррациональных функций.

1)Интегрирование дробей вида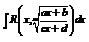

Любой интеграл такого вида рационализируется с помощью подстановки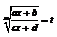

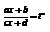
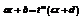
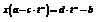
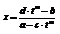
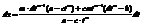
2)Интеграл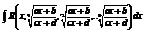

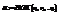, тогда интеграл станет рациональной функцией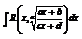

5, 1) Интегрирование правильных рациональных дробей 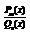m<n

Для интегрирования таких дробей многочлен стоящий в знаменателе разлагаем на действительные множители типа: х-а, или 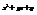, причем множители второго типа не разложимы, тогда разложение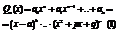

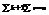
Теорема: всякую правильную рациональную дробь 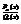, 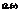разложен на множители в виде (1) можно представить в виде простых дробей в виде: 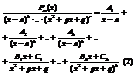Теорема утверждает, что разложение (2) возможно, но точных значений коэффициентов 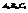не даёт. Для практического нахождения этих коэффициентов можно поступить следующим образом:

1) Метод «неопределенных коэффициентов»

В разложении (2) дроби справа приводятся к общему знаменателю (такому же, как и слева), т.к. дроби слева и справа равны, при равных знаменателях, то должны быть равны и их числители, т.к. в числителях стоят многочлены степени не больше чем n-1 то получим n линейных алгебраических уравнений (приравнивая коэффициенты при равных степенях) для нахождения n неизвестных коэффициентов 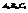. После нахождения коэффициентов правильную рациональную дробь можно проинтегрировать как сумму простых дробей.

2) Метод «придания конкретного значения»

Задаём 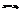из которого возможно найти один из коэффициентов. Имеет смысл применять при наличии множителя первого типа

3) Комбинированный метод

Часть переменных находится по первому способу, часть по второму.

2) Интегрирование произвольных рациональных дробей

Всякая рациональная дробь, представленная в виде 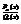, причем, если 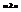, то дробь

не правильная, в этом случае необходимо выделить целую часть, после чего дробь

можно записать в виде: 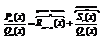, т.о. образом рациональная дробь

интегрируется в любом случае в конечном виде, причем в результат войдут только

рациональные дроби, логарифмы и 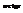.