Отклонение эмпирического распределения от нормального.
Хотя многочисленные био.признаки и подчиняются нормальному распределению, эмпирическая кривая распределения, построенная на основании вариационного ряда, часто отклоняется от кривой нормального распределения.
Наиболее характерным является отклонение вершины эмпирической кривой влево/вправо от значения средней арифметической x̅ выборочной совокупности. Для кривой нормального распределения моды, медианы и средней арифметической совпадают (Mo=Me= x̅). (Мода –это наиболее часто встречающаяся величина. Медианаявляется серединой вариационного ряда, по обе стороны от нее находится одинаковое кол-во вариант). При смещении вершины эмпирического распределения влево (Мо˂ x̅) имеет место правосторонняя асимметрия, при смещении вправо (Мо˃ x̅) – левосторонняя асимметрия. Для количественной характеристики степени асимметрии используют коэффициен асимметрии Аs, численно равный отношению центрального момента третьего порядка (среднего значения кубов отклонений вариант от средней арифметической) к кубу среднего квадратического отклонения: As= ∑p(xi - x̅)3/nσ3
Если вершина сдвинута влево от значения x̅, коэффициент As˃0, поэтому такую асимметрию называют положительной. При смещении вершины вправо As˂0, асимметрию называют отрицательной. Коэффициент асимметрии является неименованной величиной, абсолютное значение которой колеблется от 0 до 1. Асимметрия считается незначительной, если As≤0,2.
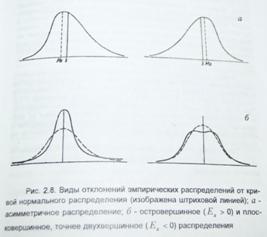 .Не менее характерным является смещение вершины эмпирического распределения вверх по отношению к кривой нормального распределения (островершинное распределение) или вниз (плосковершинное распределение). Для оценки степени этого отклонения применяется коэффициент эксцесса
.Не менее характерным является смещение вершины эмпирического распределения вверх по отношению к кривой нормального распределения (островершинное распределение) или вниз (плосковершинное распределение). Для оценки степени этого отклонения применяется коэффициент эксцесса
Ех=(∑(xi - x̅)4 / nσ4) -3.
При кривой нормального распределения Ех=0; при островершинном распределении Ех˃0 и может иметь самое различное значение; при плосковершинном распределении Ех˂0, его предельное значение равно минус двум.
Асимметрия и эксцесс могут встречаться одновременно в одном эмпирическом распределении.
Причиной ложной асимметрии вариационного ряда может быть «неудачный» выбор границ классов, классового интервала.
При изменении их такая асимметрия исчезает. Если же этого не происходит, то асимметрия обусловлена био.причинами, в частности, превалирующим односторонним влиянием факторов. Вероятно, симметричное распределение имеет место при стационарном состоянии био.систем, в процессе же изменения признака под воздействием различных причин распределение становится асимметричным.
Вычисление теоретических частот эмпирических распределений.
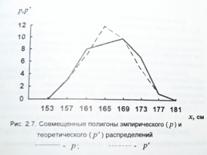
Нахождение теоретических частот вариационного ряда называется выравниванием эмпирического распределения. Значение теоретической частоты определяется по формуле: p′=(n‧i/σ)‧f(t), где где n – объем эмпирической выборки; i – классовый интервал; t – нормированное отклонение.
Значение f(t) является табличным, причем знак при величине t на эту функцию не влияет, т.е. f(t) = f(-t)
При постарении графиков полигона эмпирического распределения (p) и теоретического распределения (p′) в единых осях, чаще всего свидетельствуют о достаточно близком к нормальному характере варьирования эмпирических значений вариант, при небольшом расхождении графиков.