Производные тригонометрических функций.

А. Производная функции y = sinx выражается формулой .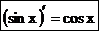

В случае сложной функции u = u(х) получим формулу .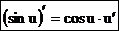

Б.Производная функции y = cosx выражается формулой .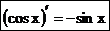

В случае сложной функции u = u(х) получим формулу .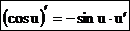

В.Производная функции y = tgx выражается формулой 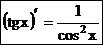, где .

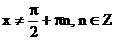В случае сложной функции u = u(х) получим формулу .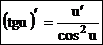

Г.Производная функции y = ctgx выражается формулой 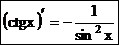,где .

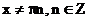В случае сложной функции u = u(х) получим формулу .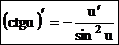

Производные обратных тригонометрических функций.

А.Производная функции y = arcsinx, |x|£1, выражается формулой .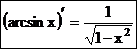

В случае сложной функции u = u(х) получим формулу .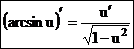

Б.Производная функции y = arccosx, |x|£1, выражается формулой .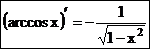

В случае сложной функции u = u(х) получим формулу .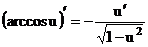

В.Производная функции y = arctgx выражается формулой .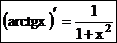

В случае сложной функции u = u(х) получим формулу .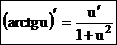

Г.Производная функции y = arcctgx выражается формулой .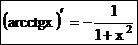

В случае сложной функции u = u(х) получим формулу .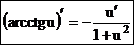

Пример. Вычислить производные функций:

1) 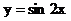; 2) .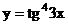

Решение

1)

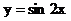
Производную сложной функции вычисляем по формуле .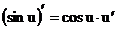

Получим .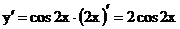

2)

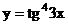
Сначала используем формулу для производной степенной функции 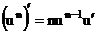, где .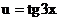

Получим

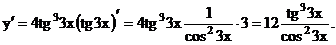
Вопрос 4. Производные высших порядков

Производная у′ = f′(х) функции у = f(х) есть так же функция от х и называется производной первого порядкаили первой производной. Возможно, что эта функция сама имеет производную.

О.4.1. Производная от первой производной функции у = f(х) называется производной второго порядка или второй производнойданной функции и обозначается одним из символов

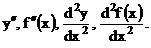
Таким образом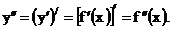

О.4.2. Производная от второй производной функции у = f(х) называется производной третьего порядка или третьей производнойданной функции и обозначается одним из символов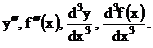

Таким образом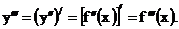

Производные, начиная со второй, называются производными высших порядков.

О.4.3. Производная от (n‒1)-й производной функции у = f(х) называется производной n-го порядка или n-й производнойданной функции и обозначается одним из символов

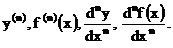
Таким образом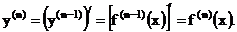

Начиная с производной 4-го порядка, производные обозначают римскими цифрами или числами в скобках.

Пример. у^V или у⁽⁵⁾ - производная 5-го порядка.

Для некоторых элементарных функций можно вывести формулы нахождения производных любого порядка.

Пример. Найти производную n-го порядка функции у = а^х.

Решение

…..,

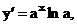
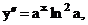
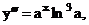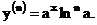
Механический (физический) смысл второй производной

Производные второго и вообще высших порядков оказываются необходимыми для определения важных понятий математики, механики, физики, а так же для более полного исследования функций.

Пусть материальная точка движется прямолинейно по закону S = S(t). Известно, что ʋ = S′(t) - скорость точки в данный момент времени t.

Можно показать, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т.е.