Вопрос 1. производная сложной и обратной функций

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

1. Производная сложной и обратной функций.
2. Правила дифференцирования.
3. Производные основных элементарных функций.
4. Производные высших порядков.

Введение

Процесс нахождения производной функции называется ее дифференцированием. При дифференцировании функции нет необходимости использовать определение производной. Вместо этого можно применять ряд правил, с помощью которых дифференцирование функций, обычно встречающихся в анализе, сводится к чисто механическим процедурам.

Вопрос 1. Производная сложной и обратной функций

Дифференцирование сложной функции

Пусть даны функции у = f(u) и u = φ(х), тогда у = f(φ(х)) - сложная функция с промежуточным аргументом u и независимым аргументом х.

Т.1.1. (производная сложной функции)

Если функция u = φ(х) имеет производную 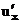в некоторой точке х, а функция у = f(u) имеет производную 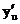в соответствующей точке u = φ(х), то сложная функция у = f(φ(х)) имеет производную 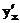в точке х, которая вычисляется по формуле

.

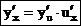Правило нахождения производной сложной функции.

Производная сложной функции по независимой переменной равна производной данной функции по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной.

Коротко: производная сложной функции равна произведению производных от функций ее составляющих.

Данное правило распространяется на случай суперпозиции трех и большего числа дифференцируемых функций. Например, если у = f(u), u = φ(v), v = g(х), то

.

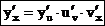Дифференцирование обратной функции

Пусть у = f(х) и х = g(у) - взаимно-обратные функции.

Т.1.2. (производная обратной функции)

Если функция у = f(х) строго монотонна на интервале (а;b) и имеет в произвольной точке х этого интервала производную 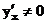, то в соответствующей точке у обратная функция х = g(у) имеет производную 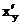, причем справедлива формула

.

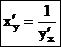Правило нахождения производной обратной функции

Производная обратной функции равна обратной величине производной данной функции.

Вопрос 2. Правила дифференцирования

1. Производная постоянной величины С равна нулю: С′ = 0.

2.Производная функции у = х равна 1: х′ = 1.

3. Если функции u = u(х) и v = v(х) дифференцируемы в данной точке х, то сумма, разность, произведение и частное этих функций (частное при условии, что v(х)¹0) так же дифференцируемы в этой точке и имеют место формулы:

, , .

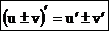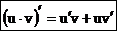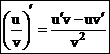Следствия

1. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные. Например, если у = u·v·w, то

.

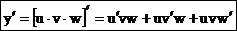1. Постоянный множитель можно выносить за знак производной:

.

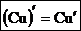1. Если С – постоянное число, то справедливы формулы:

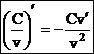и .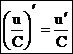

Вопрос 3. Производные основных элементарных функций

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

1. Производная сложной и обратной функций.
2. Правила дифференцирования.
3. Производные основных элементарных функций.
4. Производные высших порядков.

Введение

Процесс нахождения производной функции называется ее дифференцированием. При дифференцировании функции нет необходимости использовать определение производной. Вместо этого можно применять ряд правил, с помощью которых дифференцирование функций, обычно встречающихся в анализе, сводится к чисто механическим процедурам.

Вопрос 1. Производная сложной и обратной функций