Классификация ду с частными производными второго порядка.
Введение.
Уравнения математической физики – дифференциальные уравнения, в них входят частные производные.
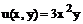
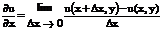
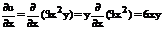
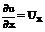
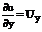
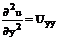
Примеры уравнений первого порядка:
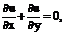
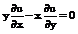 (1)
(1)
Примеры уравнений второго порядка:
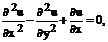
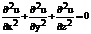 (2)
(2)
Рассмотрим простейшее уравнение:
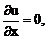
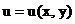 . (3)
. (3)
Очевидно, что его решение:
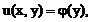 (4)
(4)
Где φ(y) – произвольная функция.
Следующий пример уравнения
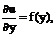 где f(y) – заданная функция. (5)
где f(y) – заданная функция. (5)
Общее решение
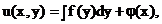 (6)
(6)
Где φ(y) – произвольная функция.
Упражнение. Проверить, что общее решение уравнения
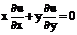 (7)
(7)
Есть
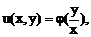 (8)
(8)
Где φ – произвольная дифференцируемая функция.
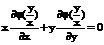
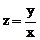
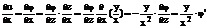
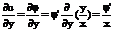
Простейшее уравнение второго порядка:
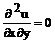 (9)
(9)
Заменим 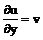 . Тогда наше уравнение принимает вид:
. Тогда наше уравнение принимает вид:
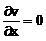 (10)
(10)
Его общее решение v=f(y). Тогда, возвращаясь к замене, получаем:
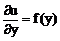 (11)
(11)
Общее решение
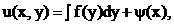 (12)
(12)
Или
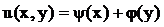 (13)
(13)
Упражнение. Проверить, что функция 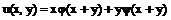 является общим решением уравнения
является общим решением уравнения
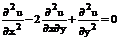 (14)
(14)
Уравнения гиперболического типа.
Основные задачи.
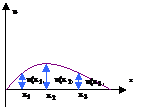 3.1.1. Поперечные колебания струны.
3.1.1. Поперечные колебания струны.
Рассмотрим струну, колеблющуюся в одной плоскости. Для описания процесса колебаний вводится функция u(x,y) – вертикальное смещение струны, так что u=u(x,y) – уравнение струны в данный момент. В нашей модели струна – гибкая упругая нить, что означает, что напряжение в струне всегда направлены по касательной к струне. Мы будем рассматривать малые колебания струны. В этом приближении можно показать, что сила натяжения струны не зависит от x и t, т.е.
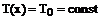 (44)
(44)
Для получения уравнения малых колебаний струны составим ее уравнение движения. Рассмотрим элемент струны от х до 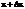 и запишем для него уравнение движения в проекциях на вертикальную ось:
и запишем для него уравнение движения в проекциях на вертикальную ось:
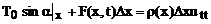 (45)
(45)
Так как мы рассматриваем малые колебания, то можно пренебрегать величинами высшего порядка малости по сравнению с 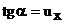
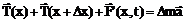
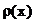 - линейная плотность струны.
- линейная плотность струны.
m – масса единицы длины струны.
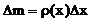
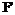 - сила, которая действует на весь элемент струны.
- сила, которая действует на весь элемент струны.
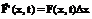
Каждая точка струны двигается по вертикали
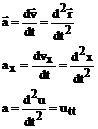
u(x,y) – смещение.
a – ускорение элемента струны.
В этом приближении
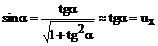
В результате уравнение движения может быть переписано в виде:
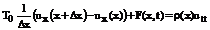 (46)
(46)
При 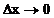 получаем
получаем
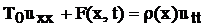 (47)
(47)
Полученное уравнение – уравнение малых поперечных колебаний струны. В случае однородной струны 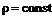 его можно переписать в виде
его можно переписать в виде
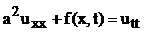 (48)
(48)
где
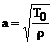
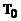 - сила
- сила
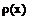 - линейная плотность струны.
- линейная плотность струны.
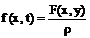 - плотность силы, отнесенная к единице массы. При отсутствии внешней силы получаем однородное уравнение
- плотность силы, отнесенная к единице массы. При отсутствии внешней силы получаем однородное уравнение
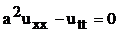 (49)
(49)
Продольные колебания стержня.
Уравнение продольных колебаний однородного стержня имеет вид:
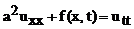 (50)
(50)
Где
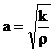 ,
,
k – модуль Юнга стержня,
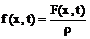 .
.
u – смещение точки стержня.
Поперечные колебания мембраны.

Мембраной называется плоская пленка, не сопротивляющаяся изгибу и сдвигу. Мы будем рассматривать только поперечные колебания мембраны. Дифференциальное уравнение таких колебаний имеет вид
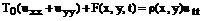 (51)
(51)
Для однородной мембраны
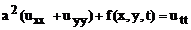 (52)
(52)
Где
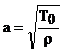
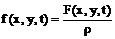
Колебания круглой мембраны.
Применим метод решения задачи о колебаниях прямоугольной мембраны к колебаниям круглой мембраны. Пусть мембрана в состоянии покоя занимает круг радиуса R с центром в начале координат. Введем полярные координаты r и φ:
x=rcos φ, y=rsin φ.
Выполняя замену переменных u(x,y,t) à u(r,φ,t) уравнение колебаний мембраны приводятся к виду

 (131)
(131)
Граничные условие будет иметь вид

Начальные условия

Будем рассматривать только осесимметричные колебания мембраны, т.е. начальные условия не должны зависеть от угла φ. Очевидно, что в любой момент времени скорости и отклонения точек будут зависеть от угла, поэтому наша задача упрощается:
 (132)
(132)
Граничные условия

Начальные условия

 |
Будем искать решение в виде
 (133)
(133)
Из краевого условия сразу находим
U(R)=0
Подставляя (133) в уравнение, получаем
 разделим на UT
разделим на UT 
 (134)
(134)
В результате приходим к уравнениям
 (135)
(135)
 (136)
(136)
В последнем сделаем замену  :
:


Подставляя в наше уравнение, получаем

 (137)
(137)
Получившееся уравнение является частным случаем уравнения Бесселя:
 (138)
(138)
Решениями последнего уравнения при заданном k называется бесселевыми функциями порядка k (цилиндрическими функциями).
Найдем решение уравнения (138). Очевидно, что оно имеет особую точку при x=0, поэтому его решение будем искать в виде степенного ряда. Для этого преобразуем его к виду:
 (139)
(139)
Записываем ряд:
 (140)
(140)
Подставляя (140) в (139) и приравнивая коэффициенты при каждой степени x нулю, получим систему уравнений
 (141)
(141)
Где l=2,3…
Предполагая, что  , находим
, находим



Из второго уравнения (141) находим, что  =0. преобразуем l-е уравнение в системе (141).
=0. преобразуем l-е уравнение в системе (141).


 (142)
(142)
Отсюда получаем рекуррентную формулу:
 (143)
(143)
С учетом найденного  =0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при
=0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при  решение обращается в бесконечность при x=0. будем рассматривать случай
решение обращается в бесконечность при x=0. будем рассматривать случай  . В результате, для четных коэффициентов получаем
. В результате, для четных коэффициентов получаем
 (144)
(144)
Применяя эту формулу m-1 раз, получим
 (145)
(145)
Полагая,

Получаем

 (146)
(146)
В результате, полученное решение  называется функцией Бесселя первого рода k-ого порядка и имеет вид:
называется функцией Бесселя первого рода k-ого порядка и имеет вид:

 (147)
(147)
Колебания круглой мембраны.
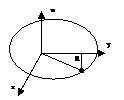 Введем полярные координаты r и φ: x=rcos φ, y=rsin φ.
Введем полярные координаты r и φ: x=rcos φ, y=rsin φ.
Выполняя замену переменных u(x,y,t) à u(r,φ,t) уравнение колебаний мембраны приводятся к виду
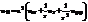
Граничные условие будет иметь вид 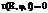
Начальные условия
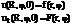
Будем рассматривать только осесимметричные колебания мембраны, т.е. начальные условия не должны зависеть от угла φ. Очевидно, что в любой момент времени скорости и отклонения точек будут зависеть от угла,
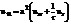
Граничные условия 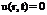
Начальные условия 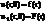
Будем искать решение в виде 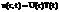
Из краевого условия сразу находим U(R)=0
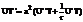
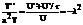
С учетом этого находим
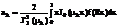
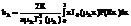
Задачи диффузии.
Концентрация – число атомов и молекул этого вещества в единице объема.
В задачах диффузии находится неизвестная функция – концентрация диффундирующего вещества, обозначаемая
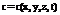
Процесс диффузии аналогичен теплопроводности, поэтому уравнение диффузии будет иметь вид
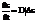 Здесь D – коэффициент диффузии.
Здесь D – коэффициент диффузии.
Начальные условия – 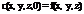
мы задаем начальную концентрацию. Краевые условия
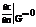 соответствует тому, что граница G непроницаема для диффундирующего вещества,
соответствует тому, что граница G непроницаема для диффундирующего вещества, 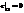 - концентрация на границе
- концентрация на границе
Введение.
Уравнения математической физики – дифференциальные уравнения, в них входят частные производные.
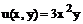
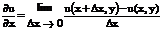
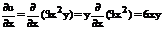
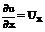
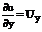
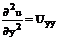
Примеры уравнений первого порядка:
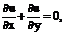
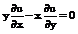 (1)
(1)
Примеры уравнений второго порядка:
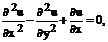
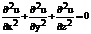 (2)
(2)
Рассмотрим простейшее уравнение:
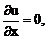
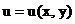 . (3)
. (3)
Очевидно, что его решение:
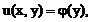 (4)
(4)
Где φ(y) – произвольная функция.
Следующий пример уравнения
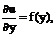 где f(y) – заданная функция. (5)
где f(y) – заданная функция. (5)
Общее решение
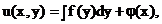 (6)
(6)
Где φ(y) – произвольная функция.
Упражнение. Проверить, что общее решение уравнения
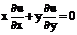 (7)
(7)
Есть
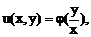 (8)
(8)
Где φ – произвольная дифференцируемая функция.
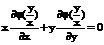
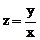
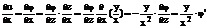
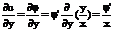
Простейшее уравнение второго порядка:
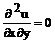 (9)
(9)
Заменим 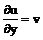 . Тогда наше уравнение принимает вид:
. Тогда наше уравнение принимает вид:
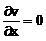 (10)
(10)
Его общее решение v=f(y). Тогда, возвращаясь к замене, получаем:
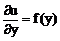 (11)
(11)
Общее решение
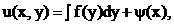 (12)
(12)
Или
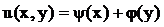 (13)
(13)
Упражнение. Проверить, что функция 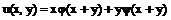 является общим решением уравнения
является общим решением уравнения
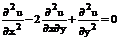 (14)
(14)
Классификация ДУ с частными производными второго порядка.
Уравнением с частными производными второго порядка с двумя независимыми переменными x, y называется соотношение между неизвестной функцией u(x,y) и ее частными производными до второго порядка включительно:
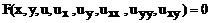 (15)
(15)
Линейное относительно старших производных уравнение
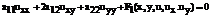 (16)
(16)
Здесь коэффициенты 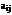 являются функциями x и y.
являются функциями x и y.
Линейное уравнение
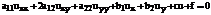 (17)
(17)
Причем a, b, c, f – зависят только от x и y. Если a, b, c, f не зависят от x и y, то (17) – однородное уравнение.
Рассмотрим вопрос о приведении уравнения (16) к наиболее простому виду. Для этого рассмотрим замену переменных:
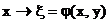 (18)
(18)
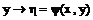 (19)
(19)
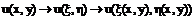
По правилу нахождения производной сложной функции:
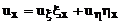 (20)
(20)
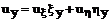 (21)
(21)
Далее
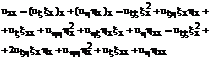 (22)
(22)
Аналогично,
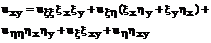
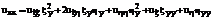
Подставляем вычисленные значения производных в уравнение (16)
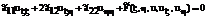 (23)
(23)
Коэффициенты при старших производных имеют вид:
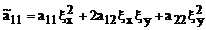 (24)
(24)
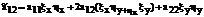 (25)
(25)
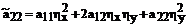 (26)
(26)
Очевидно, что наиболее простой вид рассматриваемое уравнение будет иметь, если 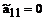 и
и 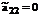 .
.
Для того, чтобы 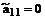 , необходимо, чтобы функция φ(x,y) была решением уравнения.
, необходимо, чтобы функция φ(x,y) была решением уравнения.
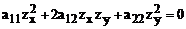 (27)
(27)
Для того, чтобы 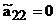 ,
, 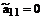 , необходимо, чтобы функция φ(x,y) была решением уравнения (27).
, необходимо, чтобы функция φ(x,y) была решением уравнения (27).
Теорема. Для того, чтобы функция z = φ(x,y) удовлетворяла уравнению (27), необходимо, чтобы соотношение φ(x,y)=С (28)
было общим интегралом уравнения
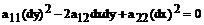 (29)
(29)
Докажем необходимость. Пусть функция z = φ(x,y) удовлетворяет уравнению (27).
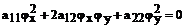
Тогда из (27) получаем:
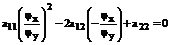 (30)
(30)
Из (28) находим:
(31) получаем, как φ(x,y)=С – берем полный дифференциал.
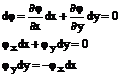
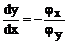 (31)
(31)
Подставляем в уравнение (30)
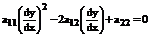
Домножаем на 
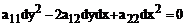 . Таким образом мы доказали необходимость.
. Таким образом мы доказали необходимость.
Докажем теперь достаточность.
Пусть φ(x,y)=С – общий интеграл уравнения (29), которое мы перепишем еще раз:
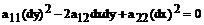
Отсюда получаем:
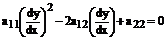
Подставляем сюда (31), находим
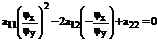
Отсюда,
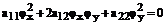 , что и требовалось доказать.
, что и требовалось доказать.
Таким образом, если 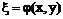 и
и 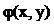 =const есть общий интеграл уравнения
=const есть общий интеграл уравнения
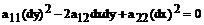 (33)
(33)
то коэффициент при 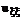 =0. если
=0. если  и
и 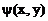 =const есть другой независимый интеграл этого уравнения, то коэффициент при
=const есть другой независимый интеграл этого уравнения, то коэффициент при 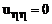 .
.
Уравнение (33) называется характеристическим, а его интегралы – характеристиками.
Уравнение (33) распадается на два:
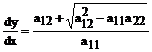 (34)
(34)
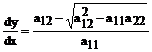 (35)
(35)
Знак подкоренного выражения определяет тип уравнения
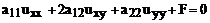 (36)
(36)
Если 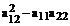 >0, то уравнение (36) – уравнение гиперболического типа. В этом случае правые части (34) и (35) действительны и различны. Получаем соответствующие общие интегралы
>0, то уравнение (36) – уравнение гиперболического типа. В этом случае правые части (34) и (35) действительны и различны. Получаем соответствующие общие интегралы 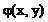 =С и
=С и 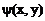 =С. Далее выполняем замену переменных
=С. Далее выполняем замену переменных
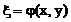 ,
, 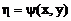 (37)
(37)
И разделив на коэффициент при 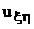 получаем уравнение вида:
получаем уравнение вида:
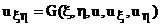 (38)
(38)
Полученное уравнение – каноническая форма уравнений гиперболического типа.
Далее выполняем замену:
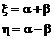 или
или 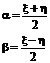
Т.е. 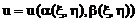
Вычисляем производные:
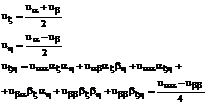
Подставляя в уравнение (38), получаем:
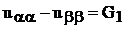 (39)
(39)
Если 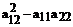 =0, то уравнение (36) – уравнение параболического типа. В этом случае уравнения (34) и (35) совпадают. Соответственно, возникает только один общий интеграл
=0, то уравнение (36) – уравнение параболического типа. В этом случае уравнения (34) и (35) совпадают. Соответственно, возникает только один общий интеграл 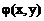 =const
=const
Выбираем переменные следующим образом:
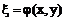 ,
, 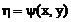 (40)
(40)
где функция 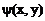 - любая независимая от φ.
- любая независимая от φ.
Рассмотрим коэффициент 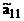 . С учетом,
. С учетом, 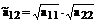 находим
находим
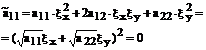 (41)
(41)
Тогда для 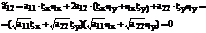 (42)
(42)
Таким образом, мы доказали, что 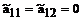
В результате мы получаем каноническую форму уравнения параболического типа:
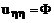
Если 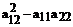 <0, то уравнение (36) – уравнение эллиптического типа.
<0, то уравнение (36) – уравнение эллиптического типа.
z=x+iy;
z=|z| 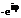
z*=x-iy
z*=|z| 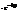
В этом случае правые части уравнений (34) и (35) комплексны. Если φ(x,y)=С – есть комплексный интеграл (34), то φ*(x,y)=С* - есть комплексный интеграл (35).
Если ввести новые переменные
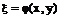 ,
, 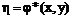
то уравнение эллиптического типа приводится к формально тому же виду, что и гиперболическое, но с комплексными переменными. Для того, чтобы перейти к действительным переменным, сделаем замену:
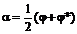
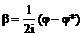 или
или
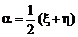
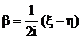
Отсюда,
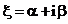
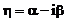
В результате наше уравнение приводится к виду
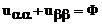 ,
,
Если из коэффициентов при старших производных составить матрицу
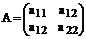 (43)
(43)
и вычислить знак определителя, то знак детерминанта матрицы А будет определять тип уравнения:
detA>0 – эллиптический.
detA<0 - гиперболический
detA=0 – параболический
