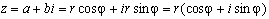Комплексные числа. Алгебраическая форма комплексного числа.

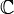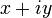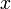Комплексные числа — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и 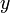— вещественные числа, 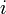— мнимая единица.

Запись комплексного числа 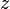в виде 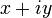, , 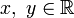называется алгебраической формой комплексного числа.

Свойства комплексных чисел. Геометрическая интерпретация комплексного числа.

Действия над комплексными числами, заданными в алгебраической форме:

Рассмотрим правила, по которым производятся арифметические действия над комплекс­ными числами.

Если даны два комплексных числа α = a + bi и β = c + di, то

α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,

α – β = (a + bi) – (c + di) = (a – c) + (b – d)i . (11)

Это следует из определения действий сложения и вычитания двух упорядоченных пар действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и вычитания комплексных чисел: чтобы сложить два комплексных числа, надо отдельно сложить их действительные части и соответственно мни­мые части; чтобы из одного комплексного числа вычесть другое, необходимо вычесть соответственно их действительные и мнимые части.

Число – α = – a – bi называют противополож­ным числу α = a + bi . Сумма двух этих чисел равна нулю: - α + α = (- a - bi) + (a + bi) = (-a + a) + (-b + b)i = 0.

Для получения правила умножения комплексных чисел воспользуемся формулой (6), т. е. тем, что i2 = -1. Учитывая это соотношение, находим (a + bi)( c + di) = ac + adi + bci + bdi2 = ac + (ad + bc)i – bd, т.е.

(a + bi)( c + di) = (ac - bd) + (ad + bc)i . (12)

Эта формула соответствует формуле (2), которой определялось умножение упорядоченных пар дей­ствительных чисел.

Отметим, что сумма и произведение двух комп­лексно сопряженных чисел являются действительными числами. Всамомделе, еслиα = a + bi, = a – bi, тоα = (a + bi)( a - bi) = a2 – i2b2 = a2 + b2 , α + = ( a + bi) + (a - bi) = (a + a) + (b - b)i= 2a, т.е.

α + = 2a, α = a2 + b2. (13)

При делении двух комплексных чисел в алгеб­раической форме следует ожидать, что частное вы­ражается также числом того же вида, т. е. α/β = u + vi, где u, v R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + bi, β = c + di, причем β ≠ 0, т. е. c2 + d2 ≠ 0. Послед­нее неравенство означает, что c и d одновременно в нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу (12) и вто­рое из равенств (13), находим:

.

Следовательно, частное двух комплексных чисел определяется формулой:

, (14)

соответствующей формуле (4).

С помощью полученной формулы для числа β = с + di можно найти обратное ему число β-1 = 1/β. Полагая в формуле (14) а = 1, b = 0, получаем

.

Эта формула определяет число, обратное данному комплексному числу, отличному от нуля; это число также является комплексным.

Например: (3 + 7i) + (4 + 2i) = 7 + 9i;

(6 + 5i) – (3 + 8i) = 3 – 3i;

(5 – 4i)(8 – 9i) = 4 – 77i;

Действия над комплексными числами в алгебраической форме.

55. Аргумент комплексного числа. Тригонометрическая форма записи комплексного числа (вывод).

Арг.ком.числа. – между положительным направлением действительной оси Х вектором изображающим данное число.

Формула тригон. Числа : 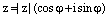,