Квадратные уравнения и неравенства

Вопросы:

1. Какое уравнение называется квадратным?

2. Что называют дискриминантом квадратного уравнения?

3. Зачем нужен дискриминант? Как его вычислить?

4. Запишите формулу решения полного квадратного уравнения.

5. В каких случаях квадратное уравнение называют неполным? Назовите виды неполных квадратных уравнений.

6. Почему важно различать неполные квадратные уравнения?

7. Какое квадратное уравнение называют приведенным?

8. Запишите теорему Виета для приведенного квадратного уравнения.

Квадратным называется уравнение, имеющее вид:

ах2+bx+c=0, а≠0

где х - неизвестная величина, а, b, с – любые действительные числа.

a,b,c – коэффициенты.

Виды квадратных уравнений:

· Полное : ах²+bx+c=0, а ≠ 0

Дискриминант: D = b² – 4ac

Если

не имеет корней имеет один корень корень имеет два корня

D < 0 D = 0 D > 0

то уравнение

D>0 имеет 2 различных корня

Формула корней: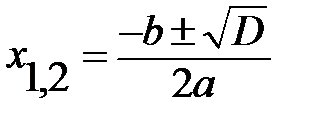

· Неполные:

а) если с=0, b≠0: ах²+bx=0, х(ах+b)=0, x=0 или ах+b =0, х=-

б) если b=0, с≠0: ах²+с=0, х²=-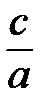

в)если b=0, с=0: ах²=0, х=0

· Приведенное – квадратное уравнение, в котором первый коэффициент равен 1: x²+px+q=0

Теорема Виета: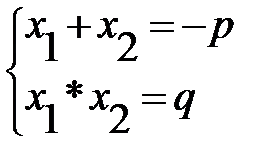

Любое квадратное уравнение при необходимости можно привести к приведенному, поделив уравнение на а≠0.

Разложение квадратного трехчлена на линейные множители:

ax² + bx + c = a(x – x₁)(x – x₂),

где х₁ и х₂ – корни уравнения

ax² + bx + c =0.

Примеры

Решить уравнения:

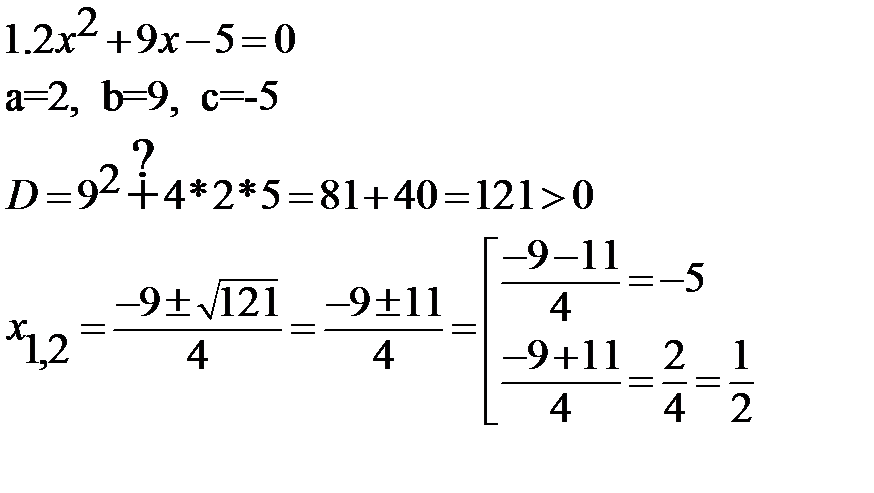
2. 3х²-7х=0, х(3х-7)=0,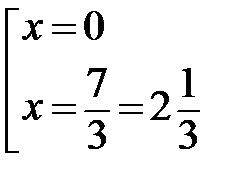

3. 2х²-50=0, 2х²=50, х²=25, х=±5

4. х²-8х-33=0

По т. Виета: х₁+х₂=8

х₁*х₂=-33=-1*33=-3*11=3*(-11).

Чтобы сумма равнялась 8, очевидно, надо взять пару: х₁=11, х₂= - 3

Самоконтроль:

Какие уравнения не являются квадратными? Квадратные уравнения приведите к стандартному виду.

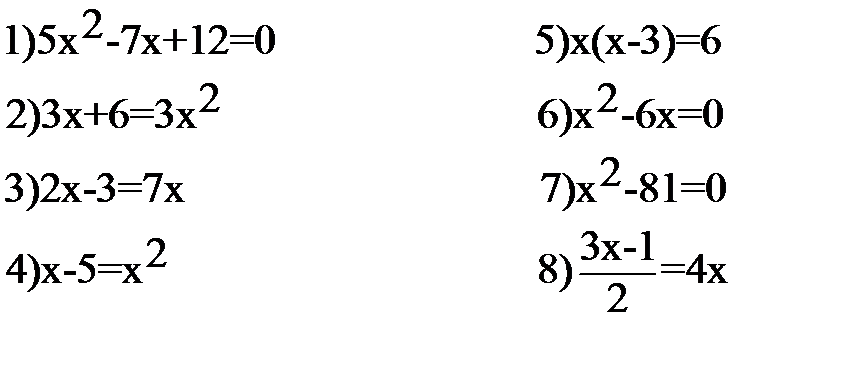
Сколько корней имеют уравнения?

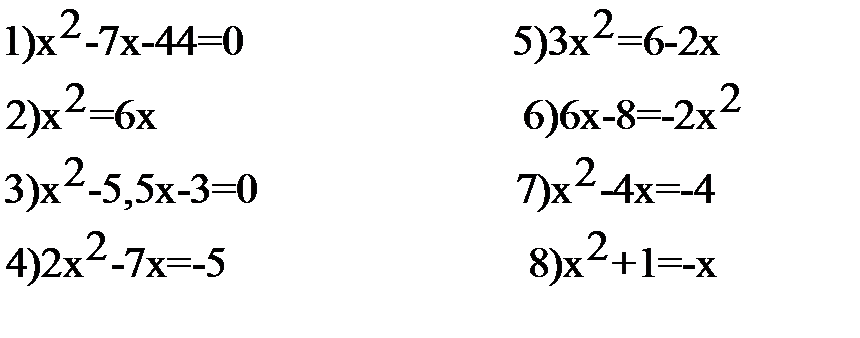
3. Приведите уравнения к стандартному виду, выпишите a, b, c, решите уравнения:

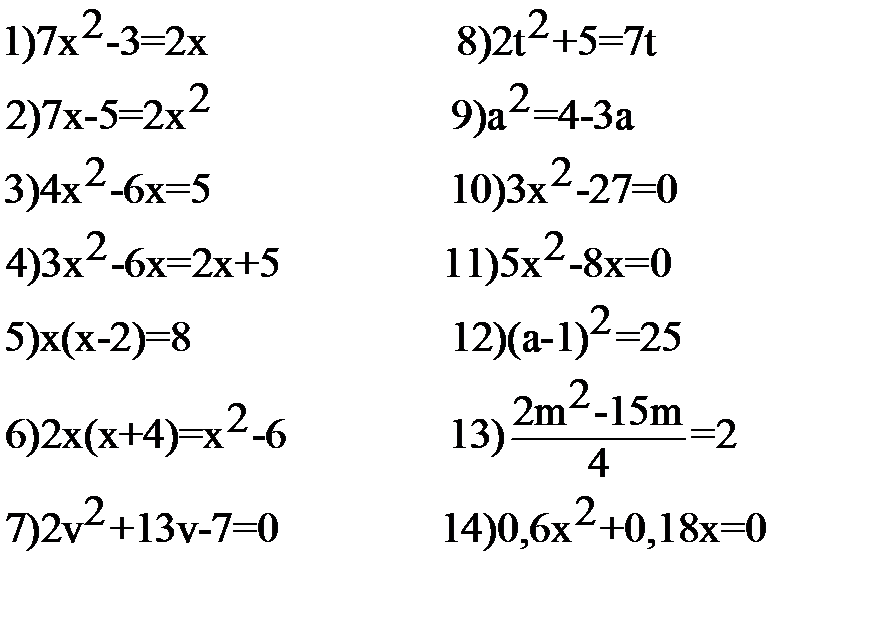
4. Не решая уравнения, найдите х₁+х_2, х₁*х_2: х²-13х+8=0

5. Сократите дробь: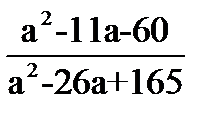

6. При каких “х» уравнение

1)имеет корни: 3х²-4х+k=0 2)имеет только один корень: 4х²-kx+4=0.

5.Решите уравнение:

6. Интересны уравнения, которые легко решаются, если при их решении воспользоваться приемом, который широко применяется в математике и называется – введение новой переменной.

Посмотрим его в примерах:

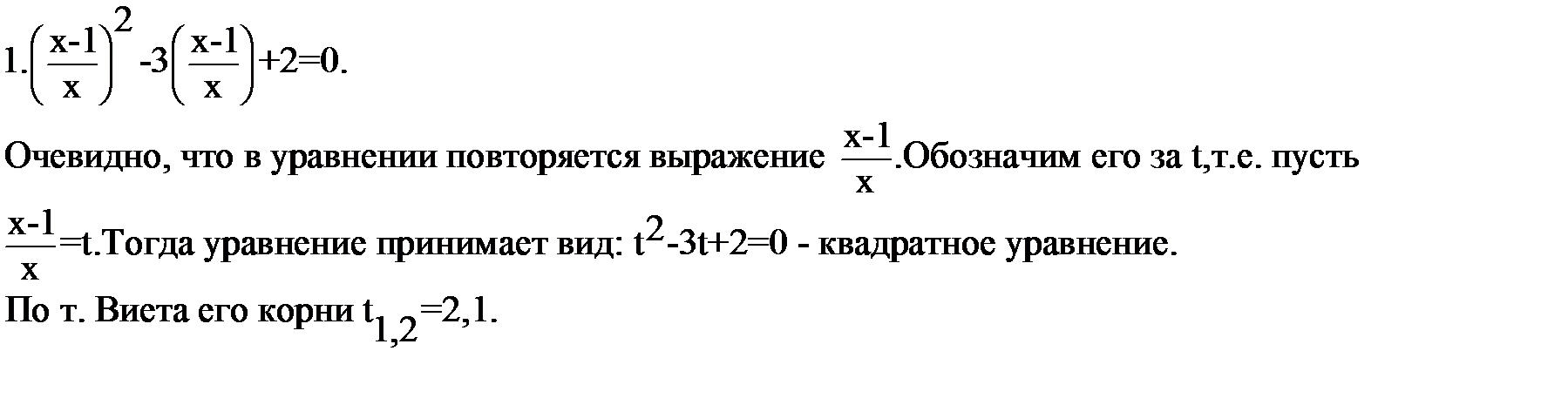Вернемся к переменной х:

Ответ: х= -1

Самостоятельно:

*

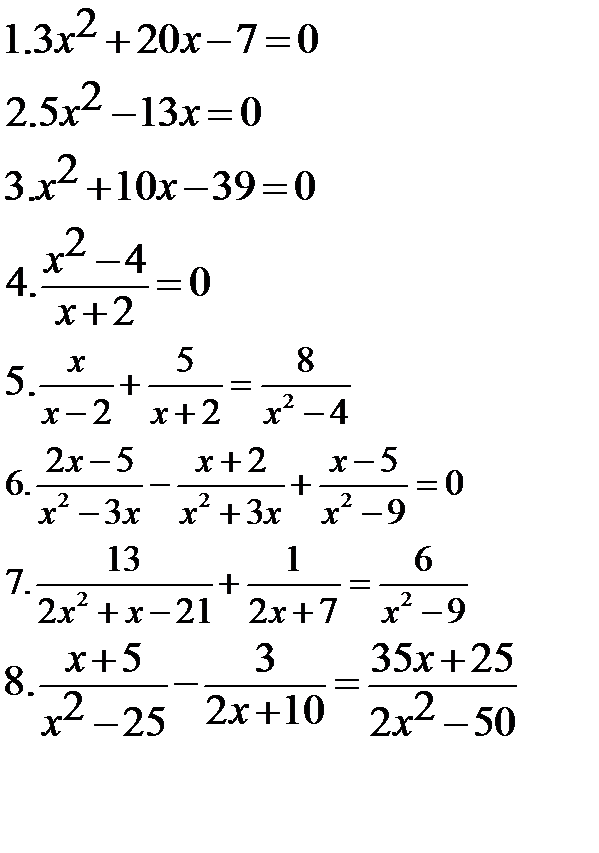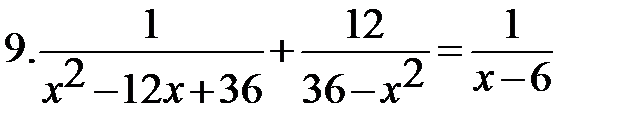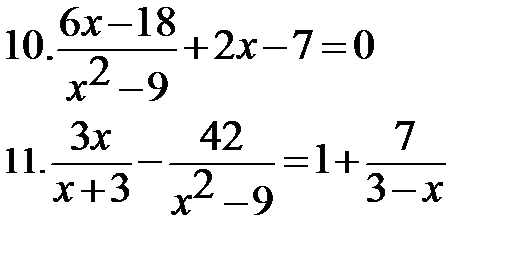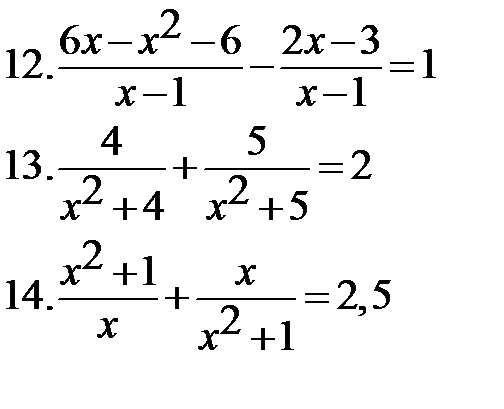*13-14: Введите новую переменную.

15.Найдите зн ачение переменной a, при котором значение выражения

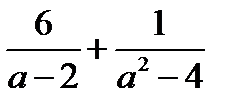равно – 3.

16.Найдите, при каком значении «у» сумма дробей 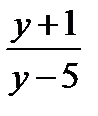и и 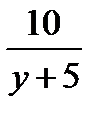их произведение принимают равные значения.

Сократите дробь:

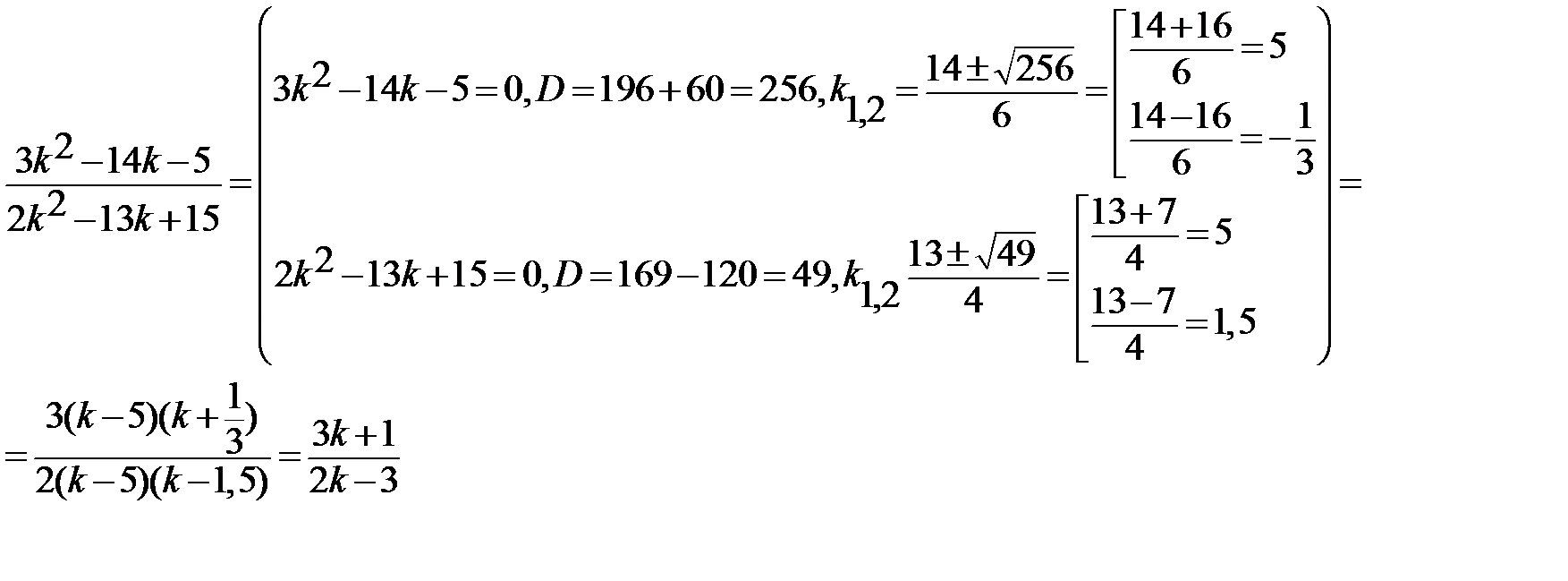
Решите квадратное неравенство (методом интервалов):

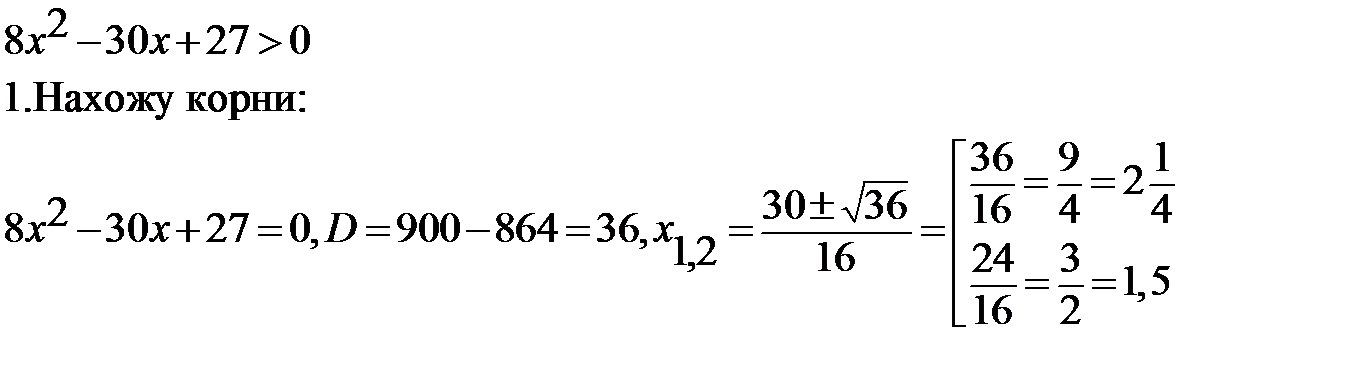
2. Наношу их на числовую ось, определяю знак левой части на каждом промежутке:

+ - +

1,5 2,25

Ответ: (-∞;1,5) (2,25;+∞)

Из материалов ЕГЭ

1. Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой 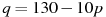. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле 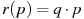. Определите наибольшую цену p, при которой месячная выручка 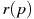составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.

2.Для одного из предприятий – монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой q =150-10p. Определите максимальный уровень цены p (в тыс.руб.), при котором значение выручки предприятия за месяц r = q*p составит не менее 440 тыс. руб.

3.Высота над землeй подброшенного вверх мяча меняется по закону 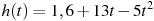, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?

4. Высота над землeй подброшенного вверх мяча меняется по закону h(t) = 1+11t-5t², где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

Решите уравнения:

5. 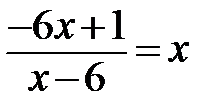. Если уравнение имеет более одного корня, то в ответ запишите меньший из них.

6. 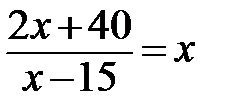. Если уравнение имеет более одного корня, то в ответ запишите меньший из них.

7. Мотоциклист, движущийся по городу со скоростью v₀=58км/ч,выезжает из него и сразу начинает разгоняться с постоянным ускорением а=16км/ч². Расстояние от мотоциклиста до города, измеряемое в км, определяется выражением S= v₀t+ 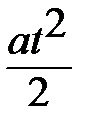. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее, чем 48 км от города.

(Ответ выразите в минутах)

(ответ: 45 минут)

Решение

1. По условию: S≤48.

2. Подставим в S данные: S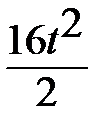=58t+ =58t+ .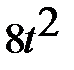

3. Решаем квадратное уравнение методом интервалов:

58t+ 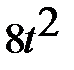≤48, 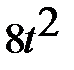+58t-48 ≤0, 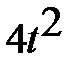+29t-24 ≤0,

D=29²+384=1225=35², t_1,2=0,75 и -8.

4. Решение неравенства 0≤ t≤0,75.

Ответ: Наибольшее значение t=0,75часа=45 минут.

8.Мотоциклист, движущийся по городу со скоростью v₀=55км/ч,выезжает из него и сразу начинает разгоняться с постоянным ускорением а=2 км/ч². Расстояние от мотоциклиста до города, измеряемое в км, определяется выражением S= v₀t+ 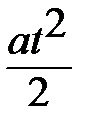. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее, чем 56 км от города.(Ответ выразите в минутах)

(ответ: 60 минут)

1.6.3. Индивидуальные задания

(Номер варианта равен остатку от деления номера по списку на 8)

ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства
1 вариант	2 вариант	3 вариант	4 Вариант
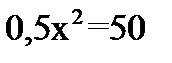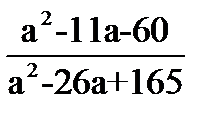1.Решите квадратные уравнения: · 2х2-х-1=0 · · 7х-х2=0 2.Не решая уравнения, найдите х1+х2, х1*х2: · х2-13х+8=0 3. Сократите дробь: · 4.Решите квадратные неравенства: · х2+5х+4≥0 · 3(х-2)(х+⅓)<0	1.Решите квадратные уравнения: · 2x2+9x+7=0 · 3x2-27=0 · 5x-x2=0 2.Не решая уравнения, найдите х1+х2, х1*х2: · х2-19х+28=0 3. Сократите дробь: · 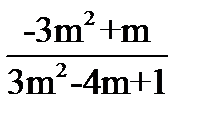4.Решите квадратные неравенства: · 2x2+7x-4<0 · 5(x+3)(x-1)≥0	1.Решите квадратные уравнения: · 2а2-9а+4=0 · 100х2-81=0 · -3х2+6х=0 2.Не решая уравнения, найдите х1+х2, х1*х2: · х2+11х-8=0 3. Сократите дробь: · 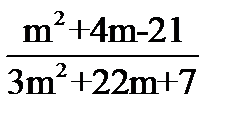4.Решите квадратные неравенства: · -3х2+5х+2≤0 · 5(х+7)(х-4)<0	1.Решите квадратные уравнения · 3a2+a=4 · 49x2=25 · -m2+4m=0   2.Не решая уравнения, найдите х1+х2, х1*х2: · х2-41х+56=0   3. Сократите дробь: · 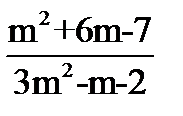4.Решите квадратные неравенства:   · 2x2-x-1>0 · (x-⅓)(x+2)≤0
ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства	ИЗ-6:Квадратные уравнения и неравенства
8 вариант	7 вариант	6 вариант	5 Вариант
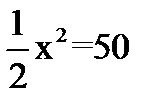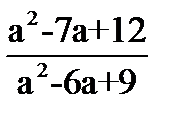1.Решите квадратные уравнения: · 2х2+5х-3=0 · · x=х2 2.Не решая уравнения, найдите х1+х2, х1*х2: · х2+3х-9=0 3. Сократите дробь: · 4.Решите квадратные неравенства:   · х2-7х+12≥0 · 3(х-4)(х+2)<0	1.Решите квадратные уравнения: · 2x2+9x+7=0 · 4x2-64=0 · 8x+x2=0 2.Не решая уравнения, найдите х1+х2, х1*х2: · х2-10х+2=0   3. Сократите дробь: · 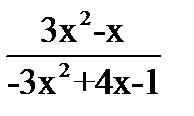4.Решите квадратные неравенства:   · 2x2-9x+4>0 · -2(x-3)(x+1)≥0	1.Решите квадратные уравнения: · 2а2-9а+4=0 · 81х2-36=0 · -5х2+х=0   2.Не решая уравнения, найдите х1+х2, х1*х2: · х2+15х+26=0   3. Сократите дробь: · 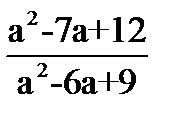4.Решите квадратные неравенства:   · 3х2-5х-2≤0 · (х-7)(х+6)<0	1.Решите квадратные уравнения · 3x2+x-4=0 · 36x2-25=0 · m2-9m=0   2.Не решая уравнения, найдите х1+х2, х1*х2: · х2-31х+25=0     3. Сократите дробь: · 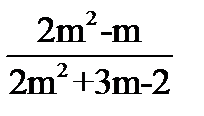4.Решите квадратные неравенства: · 3x2-4x+1<0 · -3(x-⅓)(x+2)≤0