Тема 1: Повторение школьного курса
Колледж Туризма и гостиничного Сервиса
Санкт-Петербурга
О. А. Малышева
Учебно-методическое пособие
по дисциплине
Математика
Повторение школьного курса
для студентов, обучающихся по специальностям СПО
социально-экономического и технического профиля на базе основного (общего) образования:
43.02.11 Гостиничный сервис
43.02.10 Туризм
43.02.01Организация обслуживания в общественном питании
19.02.10 Технология продукции общественного питания
Санкт-Петербург
Автор: О.А. Малышева
Рецензенты:
Лавров А.Г.- кандидат технических наук, доцент кафедры математики и информатики Санкт-Петербургского института гостеприимства.
Пособие предназначено для студентов, обучающихся по указанным специальностям.
В пособии рассматриваются базовые темы школьной программы, знание которых необходимо для дальнейшего успешного усвоения программного материала.
По каждой теме кратко излагаются теоретические основы, приводятся примеры решения стандартных задач, предлагаются индивидуальные задания для самостоятельной работы.
Пособие содержит демонстрационный вариант входного тестирования, демонстрационный вариант заключительной контрольной работы.
Пояснительная записка
Учебно-методическое пособие по математике «Повторение школьного курса» разработано с целью организовать быструю эффективную работу по повторению материала программы по математике для основной (общей) школы, предназначено для специальностей
43.02.11 Гостиничный сервис
43.02.10 Туризм
43.02.01Организация обслуживания в общественном питании
19.02.10 Технология продукции общественного питания
Как показывает практика многолетнего преподавания математики на 1 курсе, уровень математической подготовки с каждым годом становится все ниже. Выпускники школы не только не имеют конкретных базовых знаний, умений, не только не владеют простейшими учебными действиями, они не имеют представления об основных направлениях в математике, которыми занимались, не понимают, что изучается в арифметике (теории чисел), что является объектом изучения в алгебре, что функции – основа математического анализа, а числа – они бывают разные и сегодня еще появляются новые.
Большинство не владеет терминологией, не имеет навыков построения формулировок, не понимает, чем отличаются друг от друга определения, теоремы, аксиомы.
Нельзя не отметить, что школьники не умеют организовать, спланировать свою деятельность, не умеют вести конспект.
В связи с этим были выбраны основные линии – числа, уравнения-неравенства, функции – и подготовлены материалы, которые максимально обеспечат эффективное повторение.
Особое внимание при этом уделено овладению основными методами изучения материала, приемами, способами решения различных задач.
Уже на этапе повторения студенты знакомятся с заданиями уровня ЕГЭ.
В результате работы с данным пособием они не только могут повторить изученное ранее, но некоторые темы изучить с нуля.
Данное учебно-методическое пособие содержит демоверсии входного тестирования и итоговой контрольной работы.
В результате работы по пособию заключительную работу большинство студентов пишет успешно.
К пособию разработан комплект слайдов.
Учебно – методическое пособие может быть использовано студентами и преподавателями для организации аудиторной и внеаудиторной работы в различной форме: групповой и индивидуальной, фронтальной, самостоятельной.
Содержание
| № | Наименование темы | страница |
| Тема 1. Повторение школьного курса | ||
| 1.1 | Множество действительных чисел. Арифметические действия во множестве действительных чисел | |
| 1.2 | Действия со степенями и корнями. | |
| 1.3 | Тождественные преобразования алгебраических выражений. | |
| 1.4 | Линейные уравнения и неравенства. | |
| 1.5 | Метод интервалов. | |
| 1.6 | Квадратные уравнения и неравенства | |
| 1.7 | Системы уравнений и неравенств. | |
| 1.8 | Функции: свойства, графики. | |
| 1.9 | Графическое решение уравнений и систем уравнений | |
| 1.10 | Демонстрационный вариант контрольной работы №1 | |
| 1.11 | Ответы | |
| 1.12 | Глоссарий |
Введение
Уважаемые студенты!
Это пособие разработано с целью оказания вам помощи при повторении базовых понятий школьного курса. Уравнения и неравенства, системы, тождественные преобразования алгебраических выражений, степени, элементарные функции, их свойства, графики – их знание необходимо для дальнейшего изучения математики.
Каждый пункт содержит необходимые теоретические сведения, примеры с решениями, задания для самостоятельной работы, элементы первой части ЕГЭ для того, чтобы вы имели представление об уровне стандартных требований. Заканчивается каждый пункт индивидуальными заданиями.
Как работать с пособием?
Значительную часть заданий мы будем подробно рассматривать в аудитории. После коллективного решения вам нужно попытаться выполнить самостоятельно некоторые задания с тем, чтобы вы сами поняли, что вам еще не понятно, могли задать вопросы. Итогом работы будет выполнение Вами индивидуальных заданий (ИЗ), которые обязательны для всех. Решения записываются в отдельную тетрадь для практических работ, сдаются на проверку, оценки ставятся в журнал.
В конце пособия есть ответы. С ними Вы можете сверять свои результаты, искать и находить ошибки.
Если Вы добросовестно повторите предлагаемый материал, то можно не сомневаться, что дальнейшее наше сотрудничество будет успешным.
Счастливого пути!
Автор.
Математические обозначения


Латинский алфавит Греческий алфавит

Входное тестирование – демонстрационный вариант
Критерии оценки:
«3» -часть1
«4» - части1,2
«5» -части 1,2,3.
Время: 90 минут.
Часть 1.
1. Вычислите: 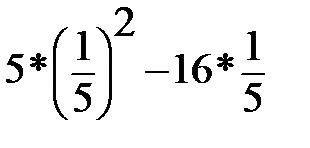
Ответ:___________________
2. Найдите значение выражения: 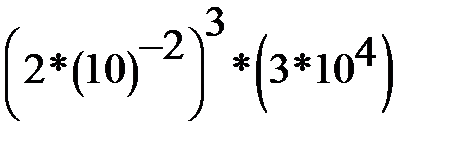
Ответ запишите десятичной дробью.
3. Упростите выражение: 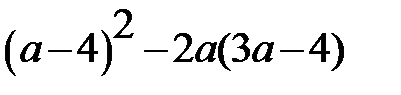
Ответ:__________________________
Решите уравнения. Запишите решение.
4. 3(2+1,5х)=0,5х+24
5. 2х2+5х+3=0
6. 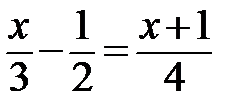
Решите системы. Запишите решение.
7. 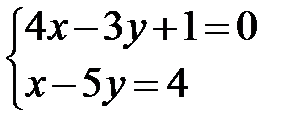
8. 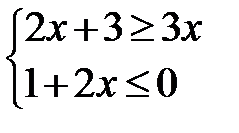
9. Какое из данных выражений не имеет смысла при х=2 и при х=3?
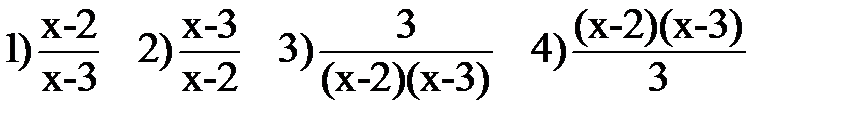
10. Построите график функции у = - 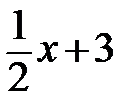 . При каких значениях «х» функция принимает отрицательные значения?
. При каких значениях «х» функция принимает отрицательные значения?
Ответ:__________________________________
Часть 2
11. Упростите: 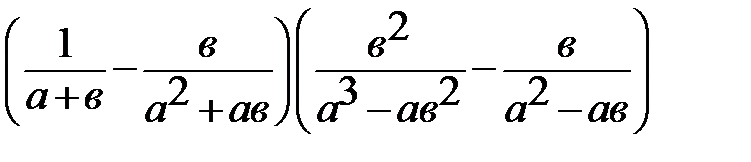
12. Решите уравнение: 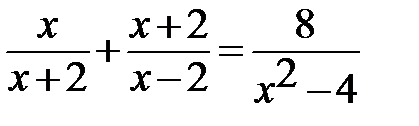
13.
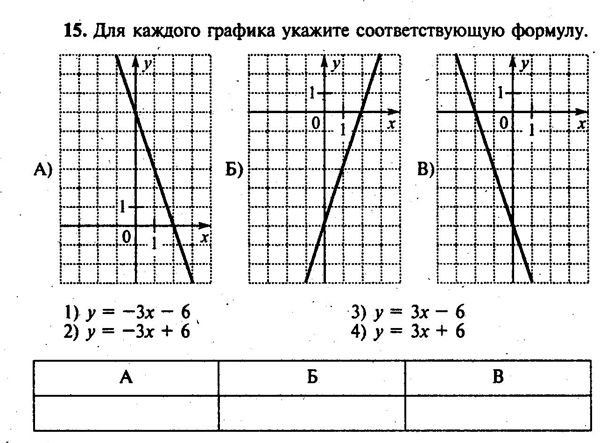
14.
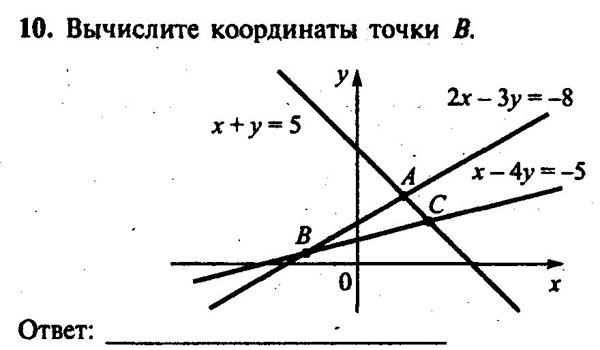
15. При каких целых положительных значениях «а» верно неравенство 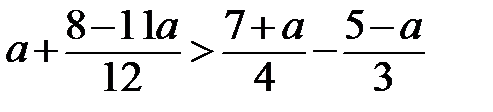 ?
?
Часть 3
16. Найдите целые решения системы неравенств:
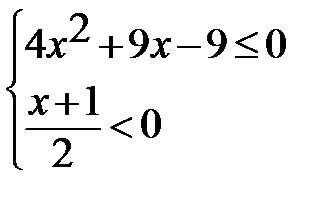
17. Найдите область определения функции: у = 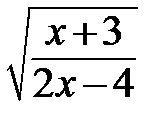
18. Найдите все целые значения «к», при которых уравнение 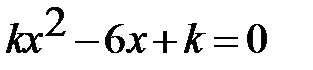 имеет два корня.
имеет два корня.
19. С помощью графиков определите, сколько решений имеет система уравнений: 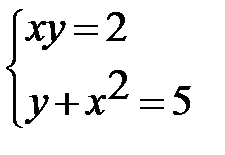
20. Постройте график функции у= - 2х2+4х-3. Запишите наибольшее значение этой функции.
Множество целых чисел.
Натуральные числа, противоположные им, число 0 образуют множество целых чисел – Z.
Целые числа могут быть записаны в виде дробей:
4=  , -5 = -
, -5 = -  .
.
Из материалов ЕГЭ
Найдите значение выражений
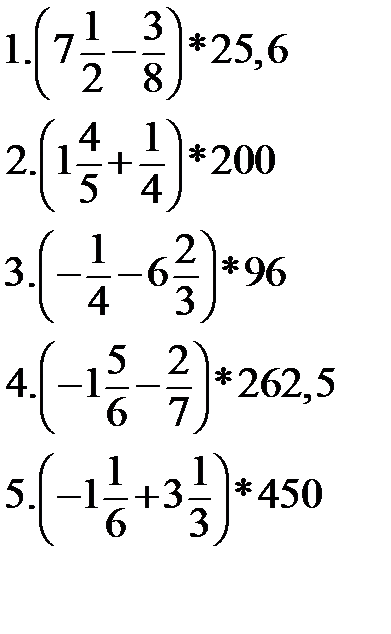 | 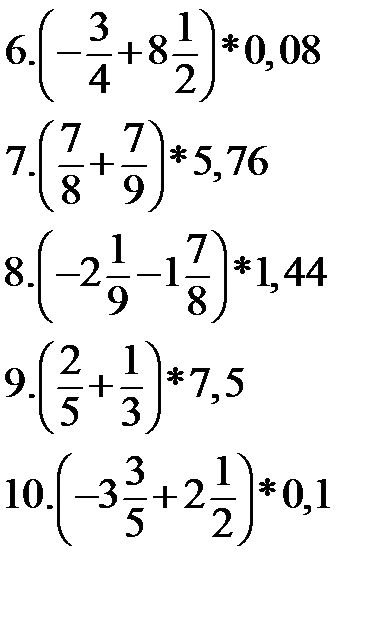 |
Решите задачи
1.Сырок стоит 8 рублей 60 копеек. Какое наибольшее количество сырков можно купить на 50 рублей? [5]
2.Больному прописано лекарство, которое нужно пить по 0,5г 3 раза в день в течение 8 дней. В одной упаковке 8 таблеток по 0,25г. Какого наименьшего количества упаковок хватит на весь курс лечения?[6]
3.Летом килограмм клубники стоит 80 рублей. Мама купила3 кг 500г клубники. Сколько рублей сдачи она должна получить с 1000 рублей?[720]
4.В пачке 500 лисов бумаги формата А4. За неделю в офисе расходуется 1300 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 7 недель? [19]
5.Для остекления дверей требуется заказать 30 одинаковых стекол в одной из 3 фирм. Площадь каждого стекла 0,25 кв.м. В таблице приведены цены на стекло и резку стекол. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена (руб. за 1 м2) | Резка стекла (руб. за 1 стекло) | Дополнительные условия |
| А | -------- | ||
| Б | -------- | ||
| В | При заказе на сумму больше 2500 руб. резка бесплатно |
Решение
Стекла требуется: 0,25*30=7,5(м2)
Фирма А: 300*7,5+25*30==3000
Фирма Б: 290*7,5+30*30=3125
Фирма В: 360*7,5=2700- самый дешевый заказ.
6.Для отделки лифтов требуется заказать 20 одинаковых зеркал в одной из 3 фирм. Площадь каждого зеркала 0,35м2. В таблице приведены цены на зеркало, резку стекла и шлифовку краев. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена (руб. за 1 м2) | Резка и шлифовка стекла (руб. за 1 стекло) |
| А | ||
| Б | ||
| В |
Ответ:6790
7. Из пункта А в пункт D ведут три дороги. Одновременно из пункта 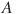 в пункт
в пункт 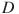 выехали грузовик, автобус и легковой автомобиль. Грузовик едет через пункт
выехали грузовик, автобус и легковой автомобиль. Грузовик едет через пункт 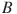 со средней скоростью 40 км/ч, автобус едет через пункт
со средней скоростью 40 км/ч, автобус едет через пункт 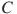 со средней скоростью 49 км/ч. По третьей дороге — без промежуточных пунктов — едет легковой автомобиль со средней скоростью 52 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам.
со средней скоростью 49 км/ч. По третьей дороге — без промежуточных пунктов — едет легковой автомобиль со средней скоростью 52 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам.
Какое транспортное средство доберётся до D позже других? В ответе укажите, сколько часов оно будет находиться в пути.
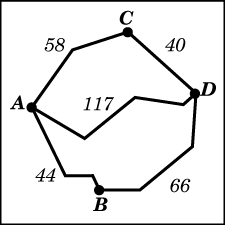
Решение
1. Известна зависимость между основными параметрами движения- пройденный путь, скорость, время:
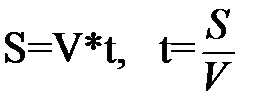 |
2. Время грузовика: t = 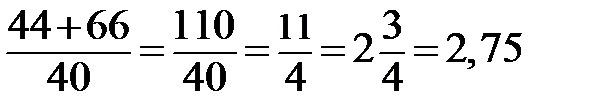
3. Время автобуса: 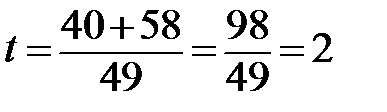
4. Время легкового автомобиля: 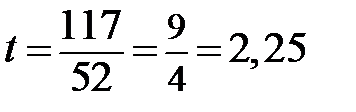
Ответ: 2 часа45минут
8. Из пункта А в пункт М ведут 3 дороги. Через пункт В едет грузовик со средней скоростью 32 км/ч, через пункт С едет автобус со средней скоростью 48 км/ч. Третья дорога без промежуточных пунктов и по ней движется легковой автомобиль со средней скоростью 56 км/ч. Из пункта А все автомобили выехали одновременно. Какой автомобиль доберется до М раньше других? В ответе укажите, сколько часов он находился в дороге.
| В |
| М |
9. Для строительства гаража можно использовать один из двух типов фундамента: бетонный или из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2400 рублей, щебень-570 рублей за тонну, мешок цемента -220 рублей за мешок. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант?
Решение
1.Для удобного обзора данных построим таблицу:
| Цена (руб.) | Бетонный | Из пеноблоков | |
| Щебень, тонна | ------- | ||
| Цемент, мешков | |||
| Пеноблоки, (м3) | ------ |
2. Стоимость бетонного фундамента: 570*2+220*20=1140+4400=5540
3. Стоимость фундамента из пеноблоков: 220*4+2400*2=880+4800=5680
4. Ответ: 5540
10. Для строительства дачи можно использовать один из двух типов фундамента: бетонный или каменный. Для фундамента из камня необходимо 7 тонн камня и 7 мешков цемента. Для бетонного фундамента необходимо 5 тонн щебня и 36 мешков цемента. Тонна камня стоит 1550 рублей, щебень-610 рублей за тонну, мешок цемента -250 рублей за мешок. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант? [12500]
11.В таблице даны тарифы на услуги трех фирм такси. Предполагается поездка длительностью 40 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ? [560]
| Фирма | Подача машины, рублей | Продолжительность и стоимость минимальной поездки*, рублей | Стоимость минуты сверхпродолжительности минимальной поездки, рублей |
| нет | |||
| бесплатно | 20 мин – 300 | ||
| 15 ин - 250 |
*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки.
12. Стоимость проездного билета на месяц составляет 580 рублей, а стоимость билета на одну поездку — 20 рублей. Аня купила проездной и сделала за месяц 41 поездку. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку? [240]
13. Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада? [8]
14. Таксист за месяц проехал 6000 км. Цена бензина 20 рублей за литр. Средний расход бензина на 100 км составляет 9 литров. Сколько рублей потратил таксист на бензин за этот месяц? [10800]
15. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? [15]
16. В доме, в котором живет Маша, 9 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Маша живет в квартире №130. В каком подъезде живет Маша? [4]
17. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 16 рублей. Если на счете осталось меньше 16 рублей, то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счете было 700 рублей. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт? [43]
18. Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков за воду платили 800 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 300 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся? [7]
19. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре? [150]
20. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа. [105]
! (Аналогичные задачи можно найти на сайтах:
· http//:mathege.ru
· открытый банк заданий по математике-2015
Действия со степенями
 | Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь. М. В. Ломоносов |
Это интересно. Оказывается, древние греки умели возводить в квадрат и в куб. Названия для второй и третьей степени числа древнегреческого происхождения: «дюнамис» — квадрат, «кюбос» — куб.
Древний Вавилон. Вавилоняне пошли дальше: составили и пользовались таблицами квадратов и кубов чисел, которыми мы пользуемся в настоящее время.
Это интересно. Широко используют степень астрономы, которым на каждом шагу приходится встречаться с огромными числами и еще производить с ними вычисления. Например, масса Солнца — 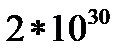 .
.
Степени также используют в биологии, химии, без них не было бы вычислительной техники.
Древние славяне тоже умели записывать большие числа, для этого у них были специальные названия: «тысяча», «тьма», «легион», «леодр».
Вопросы:
1. Какое выражение называют степенью?
2. Приведите примеры степеней с различными основаниями.
3. Какие действия со степенями можно выполнять? Опишите правила действий со степенями.
Степень
 – основание степени
– основание степени
 – показатель степени
– показатель степени
Определения степеней с различными показателями
1.Степень с натуральным показателем (n 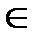 N)
N)
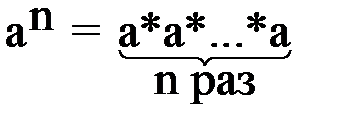 |
2.Степень с отрицательным показателем (n 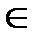 N)
N)
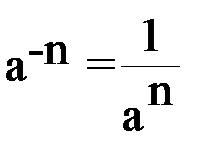 |
3.Степень с рациональным показателем (n,m 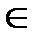 N)
N)
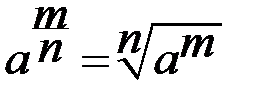 |
4. Степень с нулевым показателем
| а0=1 |
Исправьте ошибку
а) 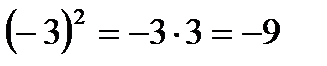 г)
г) 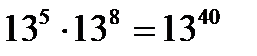 ж)
ж) 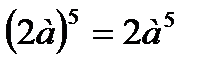
б) 
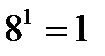 д)
д) 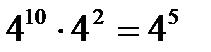 з)
з) 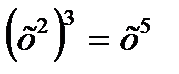
в) 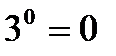 е)
е) 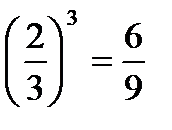 и)
и) 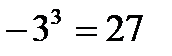
1.2.5. Индивидуальные задания-ИЗ-2
(Номер вариант равен остатку от деления номера по списку на 4)
| 1 вариант | 2 вариант | 3 вариант | 4вариант | |
1. 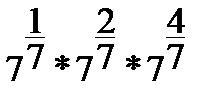 | 1. 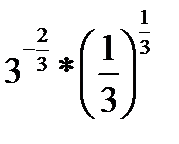 . . | 1. 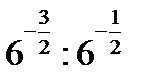 | 1. 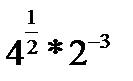 | |
2. 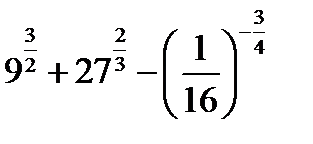 | 2. 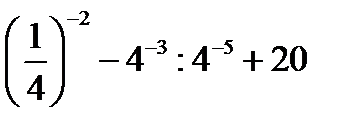  | 2. 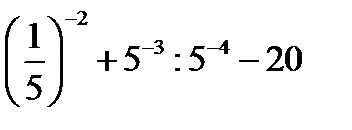 | 2. 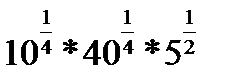 | |
3. 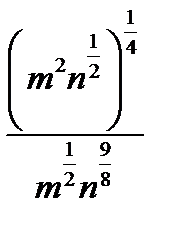 | 3. 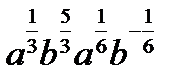 | 3. 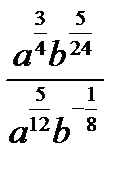 | 3.  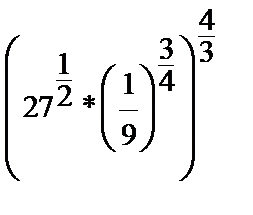 | |
4. 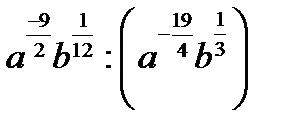 | 4. 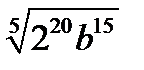 | 4. 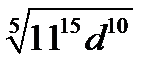 | 4. 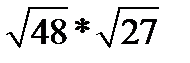 | |
5. 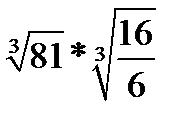 | 5. 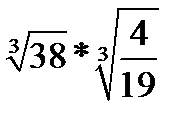 | 5. 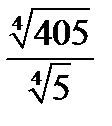 | 5. 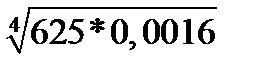 | |
Из материалов ЕГЭ
Найдите значение выражения:
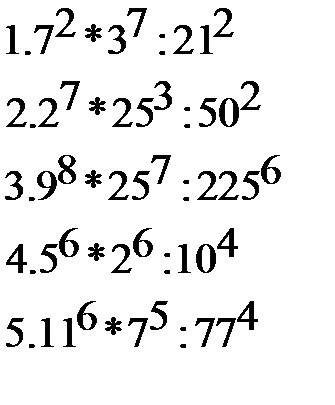 | 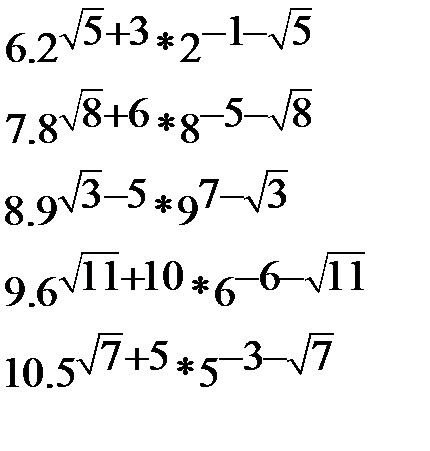 | 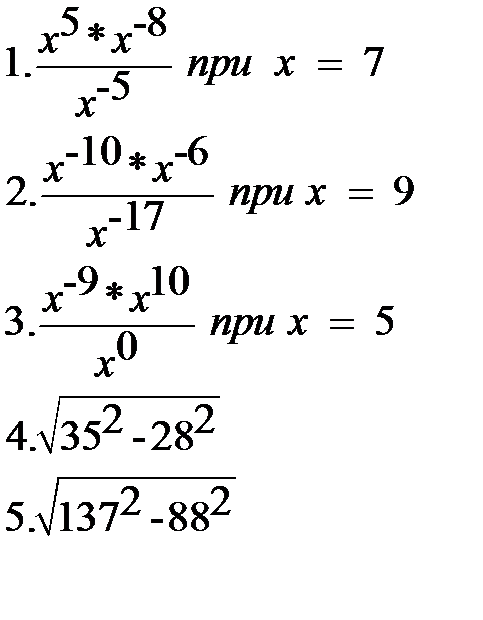 |
1.3.Тождественные преобразования алгебраических выражений
 | Франсуа Виет – юрист по образованию и математик по призванию, положивший начало алгебре как науке о преобразовании выражений, решению уравнений в общем виде, создатель буквенного исчисления |
Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в степень и извлечения корней и с помощью скобок составляются алгебраические выражения.
Примеры алгебраических выражений:
1)2а2b-3ab2(a+b); 2)a+b+ 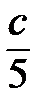 ; 3)
; 3) 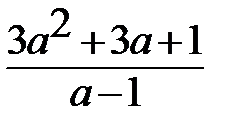 ; 4)
; 4) 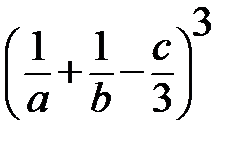 ; 5)
; 5) 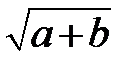
6) 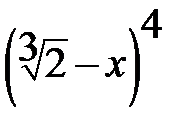 ; 7)
; 7) 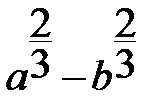
Если алгебраическое выражение не содержит деления на переменные и извлечения корня, то оно называется целым (1,2,6), в противном случае – дробным (3 и4). Если используется извлечение корня или возведение в дробную степень, то такое выражение называется иррациональным (5 и 7).
Целые и дробные – рациональные.
Преобразования выражений, не только алгебраических, нам придется в дальнейшем очень часто, поэтому важно научиться делать это хорошо.
В математике приняты следующие термины:
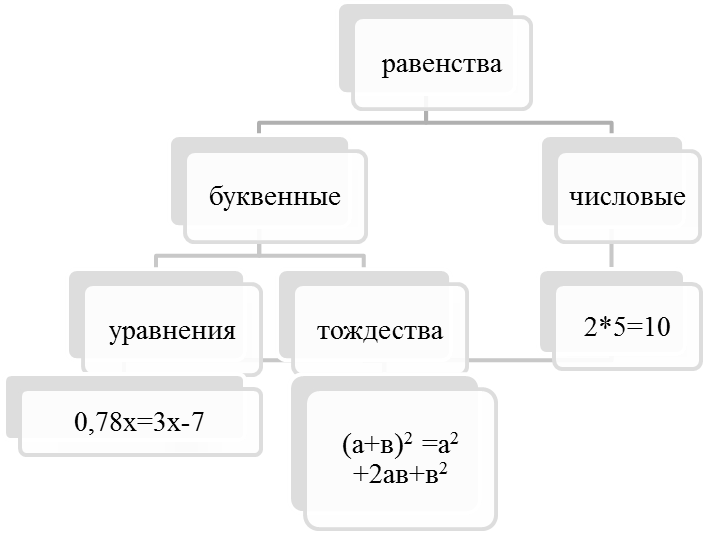
Уравнения – это равенства, которые выполняются только при некоторых значения переменных.
Тождества – это равенства, которые выполняются при всех значениях переменных.
Мы будем выполнять только тождественные преобразования, т.е. такие, при которых не изменяется значение выражения, меняется только внешний вид. Например, тождественно равны выражения: х5 и х2*х3, а+в+с и с+а+в, (2ав)2 и 4а2в2.
Примеры тождеств:
а+в=в+а, а+0=а, (а+в)*с=ас+вс, а*1=а.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения.
Основные понятия:
· Одночленом называется такое выражение, которое содержит числа, степени переменных и их произведения и не содержит никаких других действий над числами и переменными.
3а*(2,5а3), (5аb2)*(0,4c3d), x2y*(-2z)*0,75 – одночлены!!!
а+в, 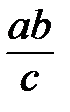 - НЕ одночлены!!! Числовой множитель – КОЭФФИЦИЕНТ.
- НЕ одночлены!!! Числовой множитель – КОЭФФИЦИЕНТ.
· Одночлены называются подобными, если они отличаются коэффициентами или не отличаются.
Например: 18х2уz3 и -8х2уz3, 3ав и 3ав – подобны.
Чтобы выполнить действия с одночленами, достаточно выполнить действия с коэффициентами. Это действие называется приведение подобных слагаемых.
· Многочлен – это сумма одночленов.
1.3.1.Основные тождественные преобразования
· Вынесение общего множителя за скобку
28х3-35х4= 7х3*4-7х3*5х=7х3(4-5х)
(Вынесение за скобку общего множителя предполагает выполнение действия деления: 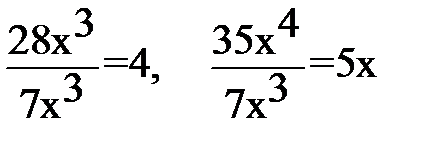 )
)
· Способ группировки
х3-3х2+5х-15=(х3-3х2)+( 5х-15)=х2(х-3)+5(х-3)=(х-3)(х2+5)
· Использование формул сокращенного умножения
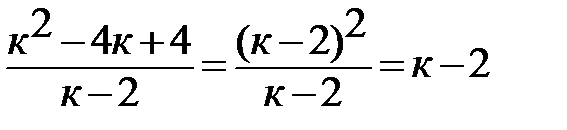
· Разложение на множители квадратного трехчлена.
4х2-5х+1=
4х2-5х+1=0,D=25-16=9>0, x1,2= 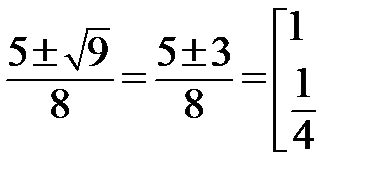
=4(x-1)(x-0,25)
Из материалов ЕГЭ
Упростите данные выражения 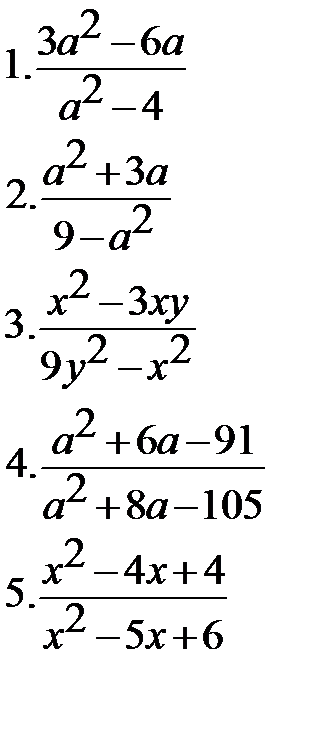 | Найдите значения данных выражений 1.(9х-16)(9х+16)-81х2+6х+30 при х=70 2.(5х-15)(5х+15)-25х2+10х-10 при х=130 3. 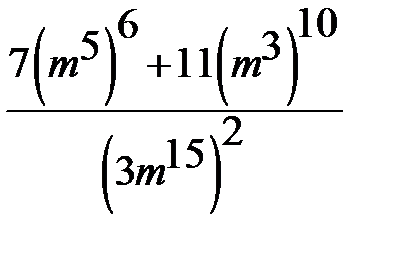 4. вычислите 4. вычислите 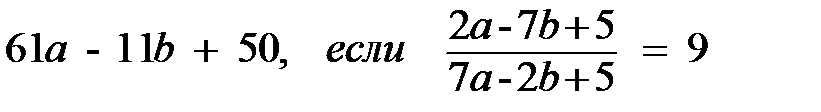 |
1.3.4.Индивидуальные задания – ИЗ-3
| Вариант 1 | Вариант 2 |
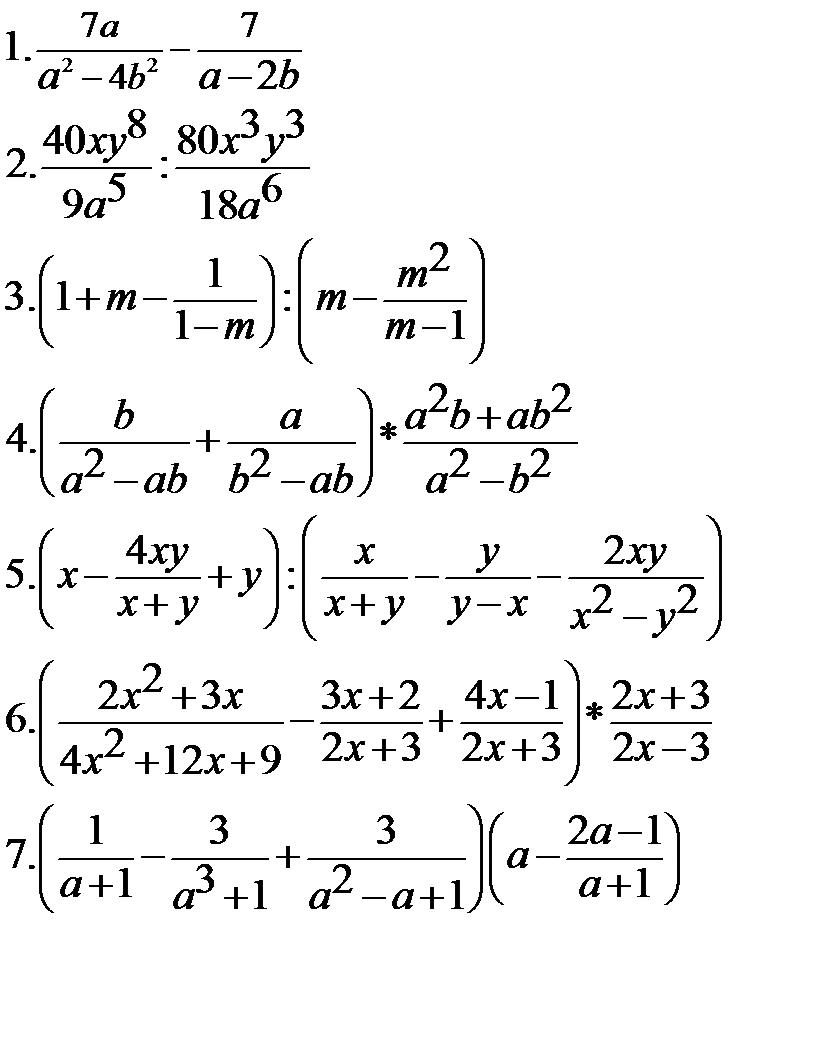 8. 8. 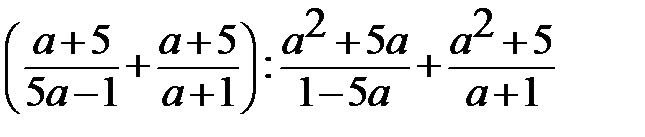 | 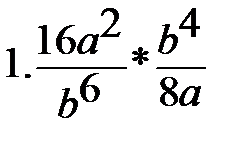 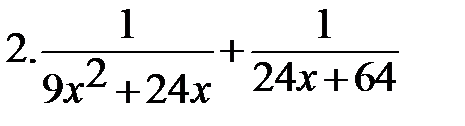 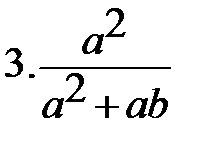 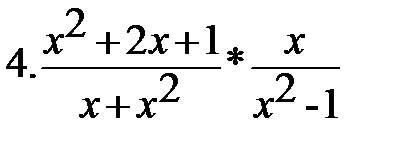 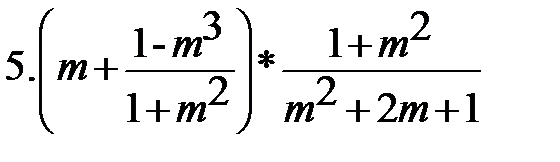 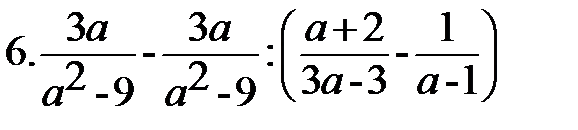 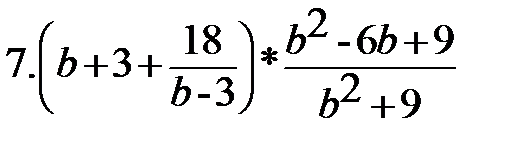 8. 8. 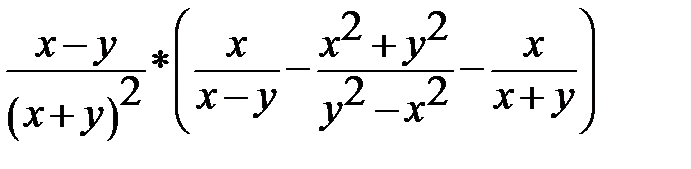 |
Вариант-3 Выполните действия: 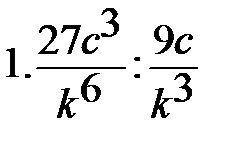 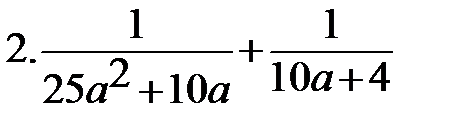 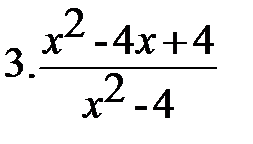 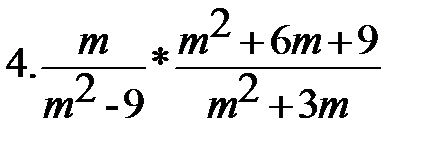 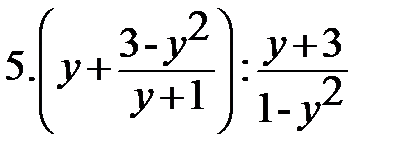 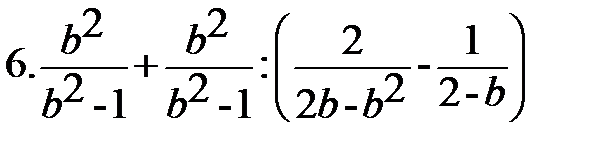 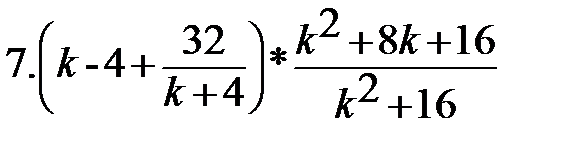 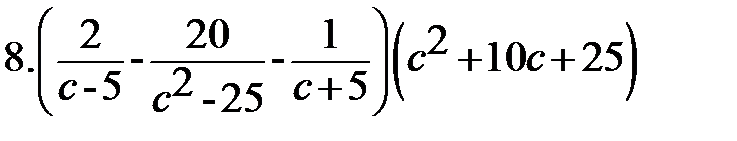 | Вариант-4 Выполните действия: 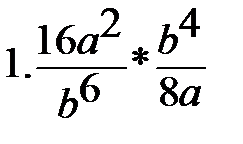 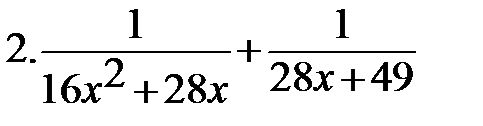 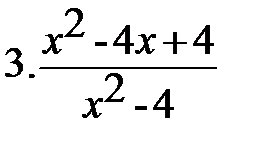 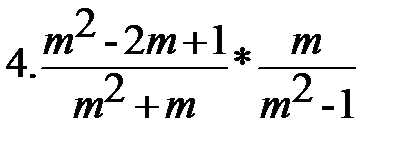 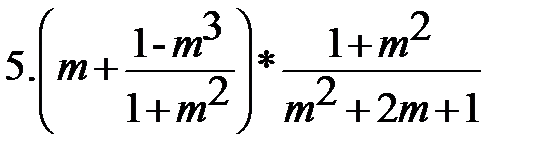 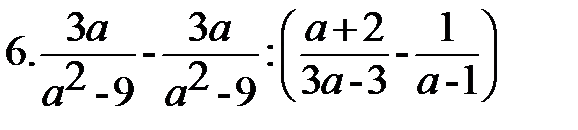 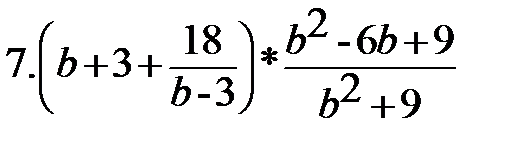 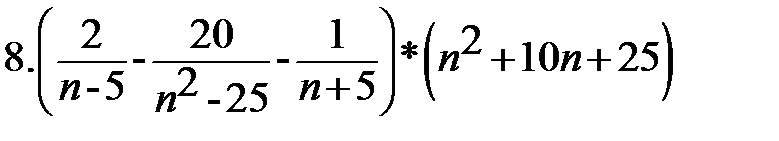 |
Линейные уравнения
Уравнения – это равенства, содержащие неизвестные величины.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Корнем уравнения называется такое число, при подстановке которого в уравнение получается верное числовое равенство.
Уравнения бывают линейные, квадратные, кубические и т.д., т.е. классификация идет по показателю степени неизвестной величины.
Линейное уравнение – это уравнение 1 степени, т.е. уравнение, в котором неизвестное в 1 степени, оно имеет вид:
| ах+в=0–линейное уравнение с одной переменной, (1) а, в – любые действительные числа. |
Чтобы решить линейное уравнение, как правило, его надо преобразовать, привести к виду(1):
Действия, приводящие к виду (1):
· Раскрытие скобок
· Приведение подобных слагаемых
· Перенос слагаемых из одной части в другую (НЕ ЗАБЫВАЯ МЕНЯТЬ ЗНАК СЛАГАЕМЫХ!!!)
Самое «трудное» уравнение для студентов
☺*x=☼, x= 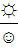 |
Примеры:
1. Простейшие
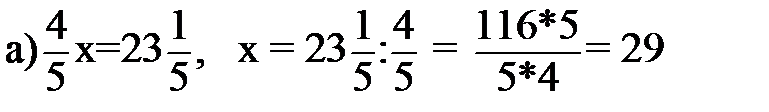
б)47-(3х-9)=110.
3х-9=47-110=-63, 3х=-63+9=-54, х= 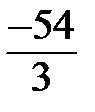 = - 18.
= - 18.
2. со скобками
0,6х-2,5(1+2х)=-0,4х+8,06.
0,6х-2,5-5х=-0,4х+8,06, 0,6х+0,4х-5х=8,06+2,5, -4х = 10,56,
х= - 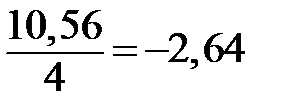
3. Дробные

в)Неизвестное - в знаменателе! 

Самостоятельно:
Решите уравнения
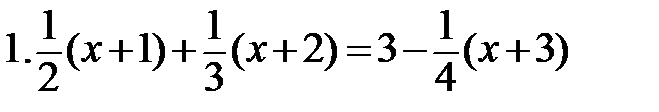 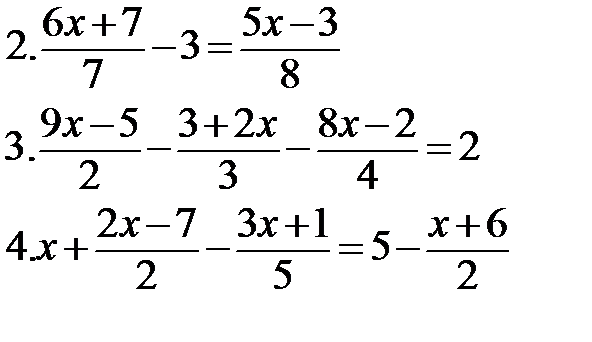 | 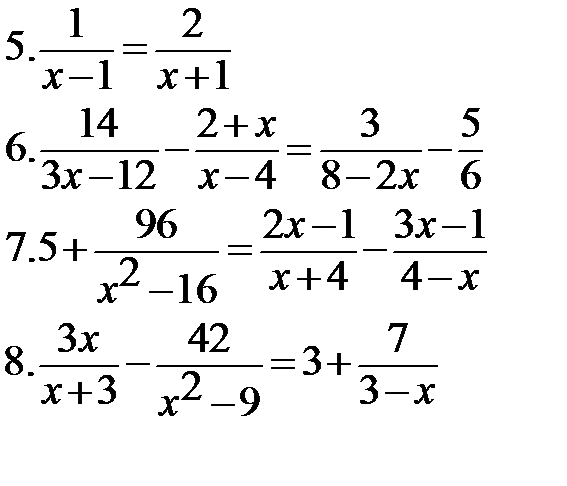 |
Линейные неравенства
Линейные неравенствас одной переменой – это неравенства вида:
ax≥b или ax≤b, где х-неизвестная,
а и b –любые действительные числа.
Всякое значение переменной, при котором неравенство обращается в верное числовое неравенство, называется решением неравенства.
Решить неравенство это значит найти все решения.
Понятия больше и меньше возникли в связи с необходимостью сравнивать предметы, величины. Понятием неравенства пользовались уже древние греки. Архимед (III век до н.э.), занимаясь вычислением окружности длины, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых».
Ряд неравенств приводит в своем трактате «Начала» Евклид.
В «Математическом собрании» Папы Александрийского также использовались знаки неравенства. Однако, все рассуждения проводили словесно, опираясь чаще всего на геометрическую иллюстрацию. Современные знаки неравенств >, < появились лишь в XVII-XVIII веках. Их ввел английский математик Т.Гарриот (1560-1621). Знаки ≥, ≤ ввел французский ученый П.Бугер (1698-1758)



При решении линейных неравенств выполняются те же преобразования, что и при решении уравнений, но возникают некоторые особенности – сложности, которые надо иметь ввиду:
· Если неравенство умножается или делится на отрицательное число, то знак неравенства меняется на противоположный
· Решать неравенства можно методом интервалов, о котором подробно позже.
Примеры:
1.2х≥7+3х, 2х-3х≥7, -х≥7│*(-1), (знак неравенства меняется на противоположный) х≤-7.
2.1,5х≥18
3.- 4х≤17+6х
4.При каких значениях «а» выражение 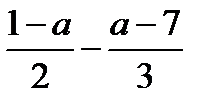 принимает отрицательные значения?
принимает отрицательные значения?
Условие означает, что должно выполняться неравенство: 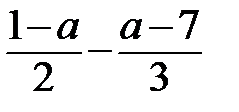 ˂0│*6,
˂0│*6,
3-3а-2а+14˂0 (почему знак неравенства не изменился?), -5а˂-17│*(-1), 5а˃17(почему знак неравенства изменился?), а˃17/5.
5. При каких значениях «х» выражение 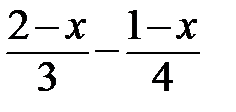 принимает положительные значения?
принимает положительные значения?
6.Решите двойное неравенство:
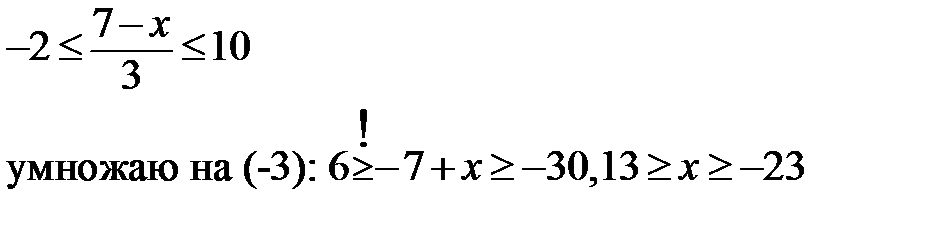
Или двойное неравенство можно записать в виде системы 2 неравенств: 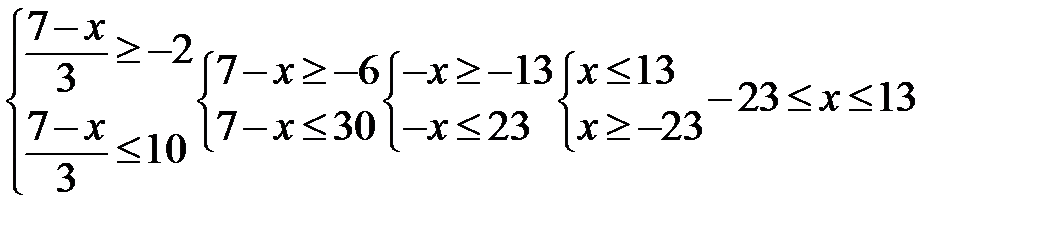
Ответ: -23≤х≤13
7. 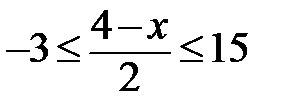
Самостоятельно:
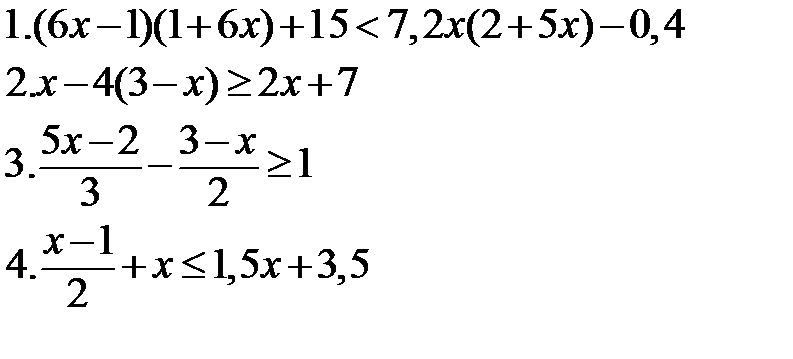 |   |
1.4.4. Индивидуальные задания
(Номер варианта равен остатку от деления номера по списку на 6)
| 1 вариант | 2 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.21-(5х-11)=12 6.(х+17)*12=804 7.0,3х-1,5(0,2х+4)=⅔*х-8,02 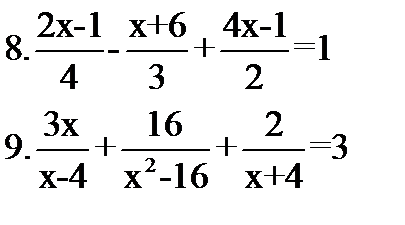 Решите неравенство: 10.5(2-3х)-4(х-7)+3(1+4х)≤10 Решите неравенство: 10.5(2-3х)-4(х-7)+3(1+4х)≤10 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.3-(4+3х)-14=0 6.13*(4-х)=26 7.5(0,4х-1)-0,4х=-21 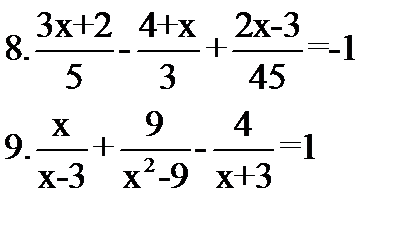 Решите неравенство: 10.(3-2х)*4+(х-2)*3-3(-х-2)≥-2 Решите неравенство: 10.(3-2х)*4+(х-2)*3-3(-х-2)≥-2 |
| 3 вариант | 4 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называетсялинейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.3-4(х+2)-(7-2х)=6 6. (5-х)*4=-16 7.0,5х-3,5(4-3х)=⅜*х-2 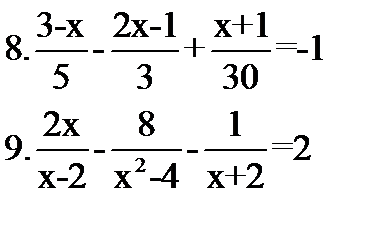 Решите неравенство: 10.3(х-4)-2(8+3х)-2(-1-х)≤ -3 Решите неравенство: 10.3(х-4)-2(8+3х)-2(-1-х)≤ -3 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным ? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.17-2(4х+9)-(5-11х)=-15 6.21*(5-13х)=-441 7.0,9х+4,5(1-2х)=-3,6 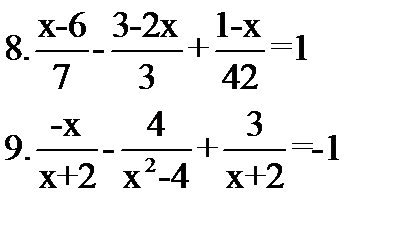 Решите неравенство: 10.2(5-х)- (-х+6)*3-5(2х+1)≥14 Решите неравенство: 10.2(5-х)- (-х+6)*3-5(2х+1)≥14 |
| 5 вариант | 6 вариант |
| ИЗ-4: Линейные уравнения и неравенства | ИЗ-4: Линейные уравнения и неравенства |
Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит - решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.1-(2х-7)-15=0 6.(х-5)*27=351 7.0,3х-2,5(0,1х-3)=-  х+3,01 х+3,01 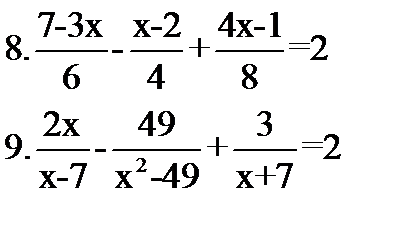 Решите неравенство: 10.(х-1)*3-(7х+9)*2-(3-х)*4≥-5 Решите неравенство: 10.(х-1)*3-(7х+9)*2-(3-х)*4≥-5 | Ответьте на вопросы: 1.Что называется уравнением? 2.Какое уравнение называется линейным? 3. Что значит – решить уравнение? 4.Что называется корнем уравнения? 5.Какую особенность имеет решение неравенств? Решите уравнения: 5.23-2(х+4)-3(5-3х)=-35 6.-43(9х+2)=473 7.0,6х-2,5(1+2х)=-0,4х+8,04 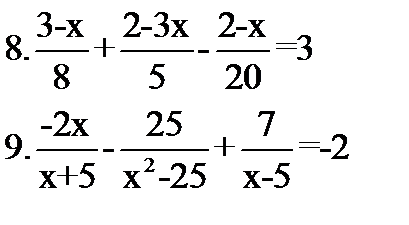 Решите неравенство: 10.4(3-2х)-2(7+3х)-5(1-х)≤11 Решите неравенство: 10.4(3-2х)-2(7+3х)-5(1-х)≤11 |
Из материалов ЕГЭ
Решите уравнения:
1.4-2х=-4х+5 2.5х-2(7+5х)=-4х-10 3. 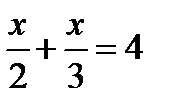 4. 4. 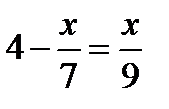 5. 5. 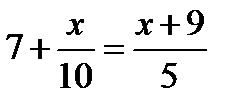 6. 6. 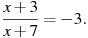 7. 7. 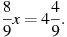 8. 8. 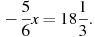 | 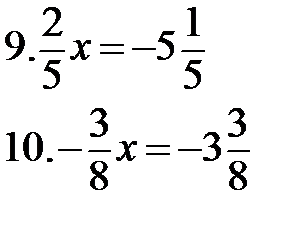 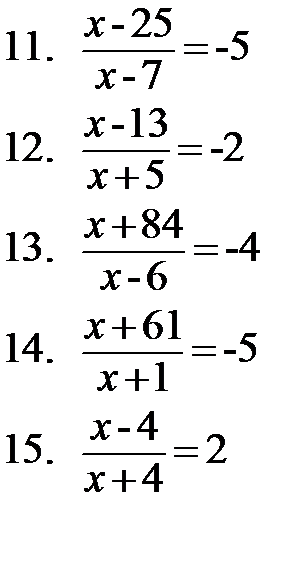 |
Решите задачи:
1.Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 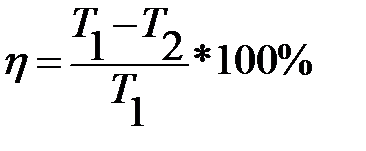 , где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 45%, если температура холодильника Т2=275К ? Ответ выразите в градусах Кельвина. (500К)
, где Т1 – температура нагревателя (в градусах Кельвина), Т2 – температура холодильника. При какой минимальной температуре нагревателя Т1 КПД двигателя будет не меньше 45%, если температура холодильника Т2=275К ? Ответ выразите в градусах Кельвина. (500К)
Решение
(задача на решение линейного неравенства)
1. По условию КПД ≥45%. Это означает, что 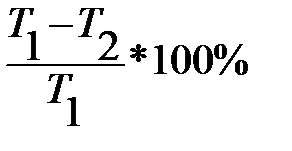 ≥45%. Это неравенство можно немного преобразовать: (1-
≥45%. Это неравенство можно немного преобразовать: (1- 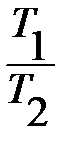 )*100≥45 или с учетом Т2=275К: 1-
)*100≥45 или с учетом Т2=275К: 1- 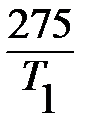 ≥0,45,
≥0,45, 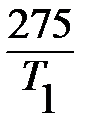 ≤0,55, Т1≥
≤0,55, Т1≥ 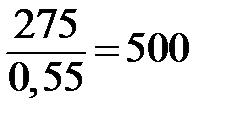 , Т1≥500К. Минимальное значение – 500К.
, Т1≥500К. Минимальное значение – 500К.
2. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой
