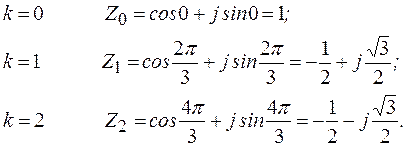Действия над комплексными числами в тригонометрической и показательной форме
Представление комплексных чисел в тригонометрической форме применяется:
а) в радиотехнике – для анализа прохождения электрического сигнала через радиотехническую цепь;
б) в системах автоматики – для определения устойчивости автоматических систем;
в) в электротехнике – для расчета целей.
Пусть задано комплексное число 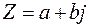 .
.
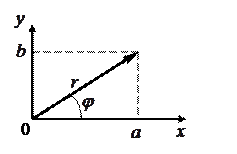
Рис. 2.1
По теореме Пифагора 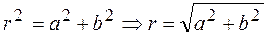 ,
,
где 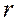 – модуль комплексного числа
– модуль комплексного числа 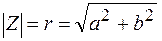 .
.
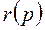 – в технической литературе может быть такое обозначение модуля.
– в технической литературе может быть такое обозначение модуля.
Модулем комплексного числа называется длина вектора, соответствующая этому числу
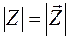 .
.
Чтобы найти конкретное комплексное число необходимо задать угол 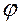 .
.
Аргументом комплексного числа называется величина угла между положительным направлением действительной оси и вектором 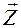 .
.
Величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной – по часовой.
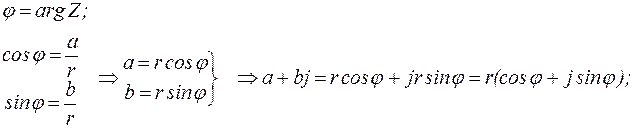
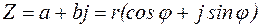 - тригонометрическая форма комплексного числа.
- тригонометрическая форма комплексного числа.
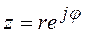 - показательная форма комплексного числа.
- показательная форма комплексного числа.
Данная форма вытекает из формулы Эйлера
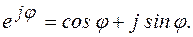
Эта система имеет бесчисленное множество решений вида
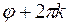 ,
,
где 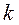 - любое целое число.
- любое целое число.
Таким образом, любое комплексное число 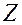 имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное
имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 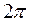 . Если
. Если 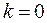 , то мы получим главное значение аргумента
, то мы получим главное значение аргумента 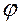 , которое и будем называть аргументом числа.
, которое и будем называть аргументом числа.
Для нахождения аргумента комплексного числа пользуемся формулой
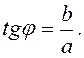
Аргумент зависит от действительной части комплексного числа.
Если 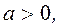 то
то 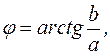 если
если 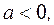 то
то 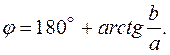
Пример 2.1
Записать комплексное число 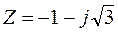 в тригонометрической и показательной форме.
в тригонометрической и показательной форме.
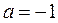 ,
, 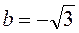 ,
,
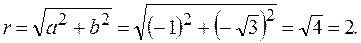
Так как 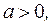 то
то 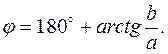
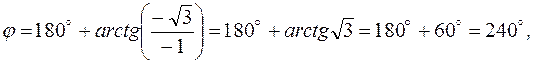
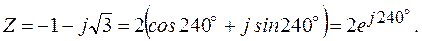
Пример 2.2
Записать комплексное число 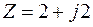 в тригонометрической и показательной форме.
в тригонометрической и показательной форме.
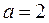 ,
, 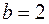 ,
,
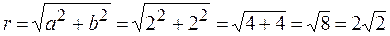 .
.
Так как 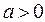 , то
, то 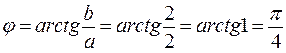 ,
,
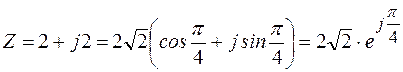 .
.
Пример 2.3
Записать комплексное число 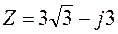 в тригонометрической и показательной форме.
в тригонометрической и показательной форме.
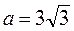 ,
, 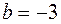 ,
,
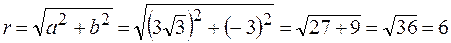 .
.
Так как 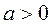 , то
, то 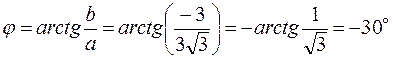 ,
,
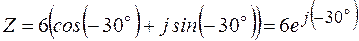 .
.
Умножение
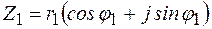
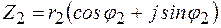
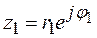
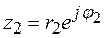
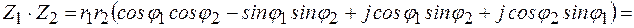
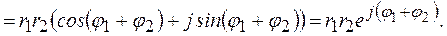
При умножении комплексных чисел в тригонометрической и показательной форме модули их перемножаются, а аргументы складываются
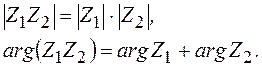
Пример 2.4
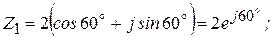
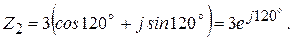
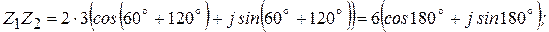
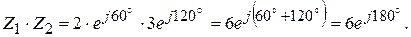
Деление
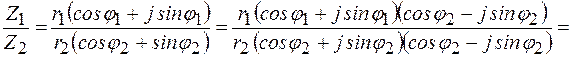
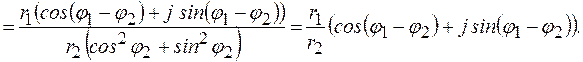
Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются
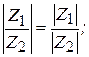
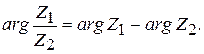
Пример 2.5
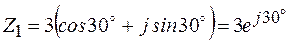 ;
; 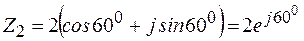 .
.
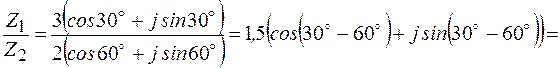
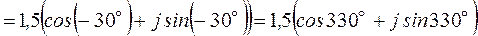 ;
;
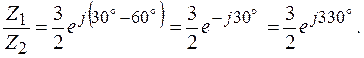
Возведение комплексного числа в степень
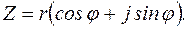
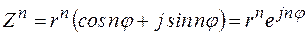 называется формулой Муавра, то есть при возведении комплексного числа в степень
называется формулой Муавра, то есть при возведении комплексного числа в степень 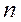 , модуль числа возводится в степень
, модуль числа возводится в степень 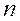 , а аргумент умножается на
, а аргумент умножается на 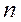 .
.
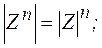
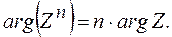
Пример 2.6
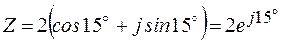 . Найти
. Найти 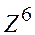 .
.
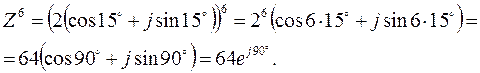
Корень n-ой степени из комплексного числа
Корнем 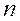 -ой степени из комплексного числа
-ой степени из комплексного числа 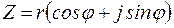 называется число,
называется число, 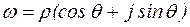 , для которого
, для которого 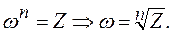
Для извлечения корня 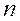 -ой степени из комплексного числа используется формула
-ой степени из комплексного числа используется формула
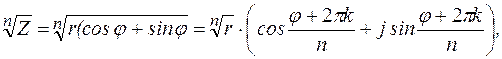
где 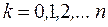 ,
,
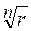 - арифметический корень.
- арифметический корень.
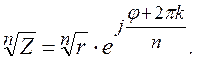
Пример 2.7
Найти 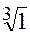 .
.
Представим число 1 в тригонометрической форме 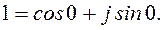
Тогда
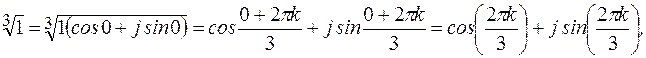
где 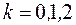 .
.