Действия над комплексными числами в алгебраической форме
КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Минск 2006
Составитель Н.Н. Чемерко
Рецензент Т.К. Гресюк
Издание утверждено на заседании кафедры М и Ф
20 марта 2006 г., протокол №8
Зав. кафедрой Л.Л. Гладков
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Комплексным числом называется выражение вида
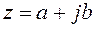 ,
,
где 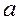 и
и 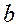 - действительные числа,
- действительные числа,
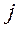 - мнимая единица.
- мнимая единица.
Число 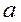 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 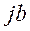 - мнимой частью.
- мнимой частью.
Комплексное число обозначается буквой 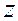 , множество комплексных чисел обозначается буквой
, множество комплексных чисел обозначается буквой 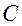 . Квадрат мнимой единицы равен
. Квадрат мнимой единицы равен 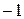 , то есть
, то есть 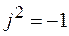 .
.
Запись комплексного числа 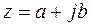 называется алгебраической формой.
называется алгебраической формой.
Два комплексных числа называются равными, когда равны их действительные части и коэффициенты при мнимой части, то есть
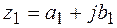 и
и 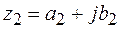
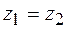 , если
, если 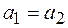 и
и 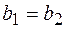 .
.
Понятие «больше» и «меньше» для комплексных чисел не определяются.
Число вида 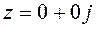 называется нулем.
называется нулем.
Число вида 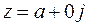 отождествляется с действительным числом
отождествляется с действительным числом 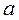 , то есть
, то есть 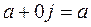 .
.
Комплексное число 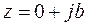 называется чисто мнимым и обозначается
называется чисто мнимым и обозначается 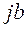 , то есть
, то есть 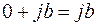 .
.
Комплексные числа 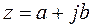 и
и 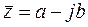 называются сопряженными.
называются сопряженными.
Произведение комплексных множителей имеет вид
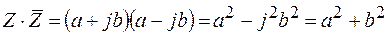 .
.
Сумма
Суммой двух комплексных чисел 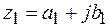 и
и 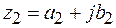 называется комплексное число
называется комплексное число
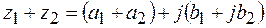 .
.
Произведение
Произведением двух комплексных чисел 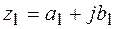 и
и 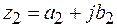 называется комплексное число
называется комплексное число
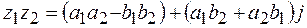 .
.
Выведем данную формулу
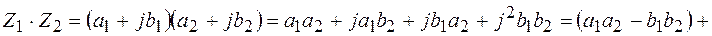
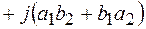 , то есть используем правило произведения многочлена на многочлен и заменяем
, то есть используем правило произведения многочлена на многочлен и заменяем 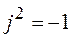 .
.
Вычитание
Вычитание вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел 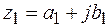 и
и 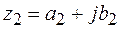 определяется формулами
определяется формулами
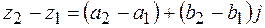 ,
,
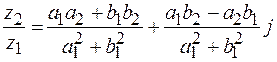 ,
,
где 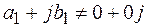 .
.
Докажем данную формулу. Для этого числитель и знаменатель умножим на число, сопряженное знаменателю и учитываем, что 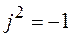
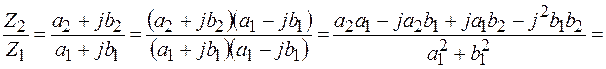
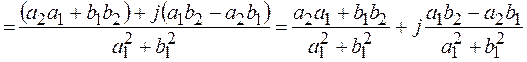 .
.
Формулы, определяющие правила действия над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия на двучленами 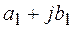 и
и 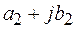 и заменить
и заменить 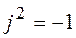 .
.
Деление
При делении комплексных чисел достаточно умножить числитель и знаменатель дроби 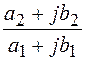 на число, сопряженное знаменателю, то есть на
на число, сопряженное знаменателю, то есть на 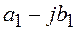 .
.
Возведение в степень
Возведение комплексного числа в степень производится по формулам возведение двучлена в степень, но при этом надо учитывать, что
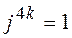 ;
; 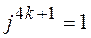 ;
; 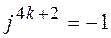 ;
; 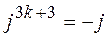 .
.
Умножение
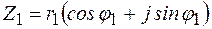
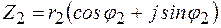
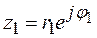
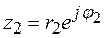
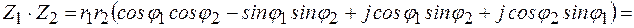
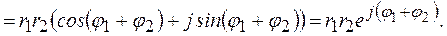
При умножении комплексных чисел в тригонометрической и показательной форме модули их перемножаются, а аргументы складываются
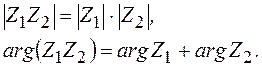
Пример 2.4
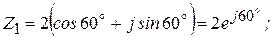
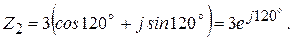
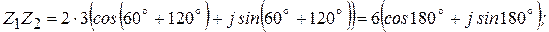
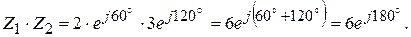
Деление
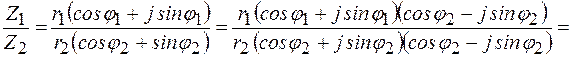
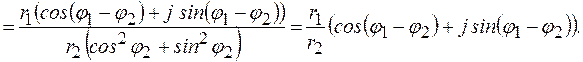
Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются
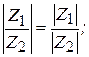
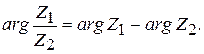
Пример 2.5
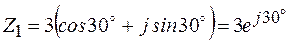 ;
; 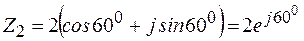 .
.
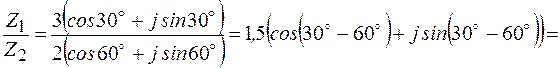
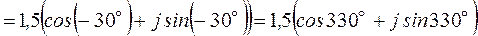 ;
;
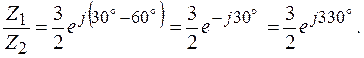
ЛИТЕРАТУРА
1 Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1980. – Гл. 10. – ÍÍ1-9.
2 Лисичкин В.Т., Соловейчик И.Л. Математика. Учебное пособие для техникумов. – М.: Высшая школа, 1991. – Гл. 2. – ÍÍ2-8.
3 Яковлев Г.Н. Алгебра и начала анализа, часть II. – М.: Наука, 1981. – Гл. 1. – ÍÍ1-3.
СОДЕРЖАНИЕ
1 ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ. 3
1.1 Сумма. 3
1.2 Произведение. 3
1.3 Вычитание. 4
1.4 Деление. 4
1.5 Возведение в степень. 4
1.6 Геометрическая интерпретация комплексного числа. 5
1.7 Поворот вектора комплексного числа. 5
Задание для самостоятельной работы. 7
2 ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФОРМЕ. 8
2.1 Умножение. 10
2.2 Деление. 10
2.3 Возведение комплексного числа в степень. 11
2.4 Корень n-ой степени из комплексного числа. 11
2.5 Переход от показательной и тригонометрической формы в алгебраическую 12
Решение примеров. 12
Задание для самостоятельной работы. 14
Литература……………………………………………………………………………………..15
План 2005/2006, поз.
Чемерко Нина Николаевна
КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Редактор Н.В. Вердыш
Подписано к печати ___________
Формат 60х84/16
Усл. печ. л ___, уч.-изд. л. ___
Тираж ___ экз. Заказ ____
Учреждение образования
«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»
220114, г. Минск, ул. Ф. Скорины 8, к. 2
КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Минск 2006
Составитель Н.Н. Чемерко
Рецензент Т.К. Гресюк
Издание утверждено на заседании кафедры М и Ф
20 марта 2006 г., протокол №8
Зав. кафедрой Л.Л. Гладков
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Комплексным числом называется выражение вида
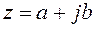 ,
,
где 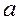 и
и 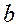 - действительные числа,
- действительные числа,
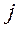 - мнимая единица.
- мнимая единица.
Число 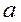 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 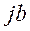 - мнимой частью.
- мнимой частью.
Комплексное число обозначается буквой 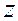 , множество комплексных чисел обозначается буквой
, множество комплексных чисел обозначается буквой 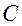 . Квадрат мнимой единицы равен
. Квадрат мнимой единицы равен 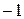 , то есть
, то есть 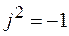 .
.
Запись комплексного числа 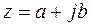 называется алгебраической формой.
называется алгебраической формой.
Два комплексных числа называются равными, когда равны их действительные части и коэффициенты при мнимой части, то есть
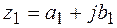 и
и 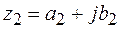
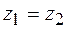 , если
, если 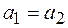 и
и 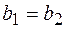 .
.
Понятие «больше» и «меньше» для комплексных чисел не определяются.
Число вида 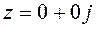 называется нулем.
называется нулем.
Число вида 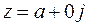 отождествляется с действительным числом
отождествляется с действительным числом 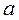 , то есть
, то есть 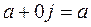 .
.
Комплексное число 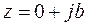 называется чисто мнимым и обозначается
называется чисто мнимым и обозначается 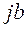 , то есть
, то есть 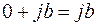 .
.
Комплексные числа 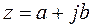 и
и 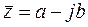 называются сопряженными.
называются сопряженными.
Произведение комплексных множителей имеет вид
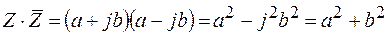 .
.
Сумма
Суммой двух комплексных чисел 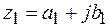 и
и 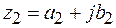 называется комплексное число
называется комплексное число
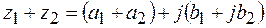 .
.
Произведение
Произведением двух комплексных чисел 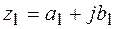 и
и 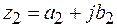 называется комплексное число
называется комплексное число
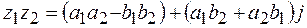 .
.
Выведем данную формулу
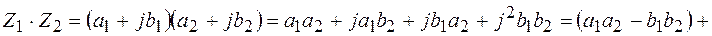
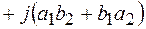 , то есть используем правило произведения многочлена на многочлен и заменяем
, то есть используем правило произведения многочлена на многочлен и заменяем 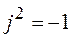 .
.
Вычитание
Вычитание вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел 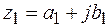 и
и 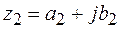 определяется формулами
определяется формулами
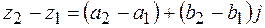 ,
,
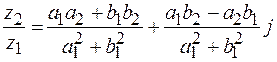 ,
,
где 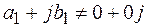 .
.
Докажем данную формулу. Для этого числитель и знаменатель умножим на число, сопряженное знаменателю и учитываем, что 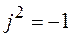
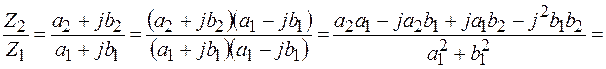
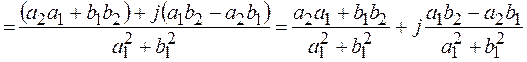 .
.
Формулы, определяющие правила действия над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия на двучленами 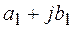 и
и 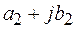 и заменить
и заменить 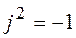 .
.
Деление
При делении комплексных чисел достаточно умножить числитель и знаменатель дроби 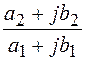 на число, сопряженное знаменателю, то есть на
на число, сопряженное знаменателю, то есть на 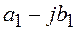 .
.
Возведение в степень
Возведение комплексного числа в степень производится по формулам возведение двучлена в степень, но при этом надо учитывать, что
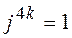 ;
; 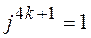 ;
; 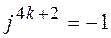 ;
; 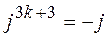 .
.
