Построение прогнозов на основе модели множественной линейной регрессии

Одной из важнейших целей построения эконометрической модели является прогнозирование поведения исследуемого процесса или объекта. Если в модели присутствует фактор времени, то прогнозирование подразумевает предсказание состояния системы в будущем. Если фактор времени в модели отсутствует, то прогнозирование величины исследуемой переменной (вычисление y_прогн) производится при некотором наборе (наборах) значений факторных переменных. Эти значения факторов (x_прогн1, x_прогн2, … , x_{прогн m}) должны быть заданы исследователем или вычислены с помощью других моделей.

Как и в случае парной регрессии вычисляются точечное и интервальное прогнозные значения исследуемой переменной.

Точечный прогноз осуществляется подстановкой прогнозного набора факторных переменных в уравнение регрессии:

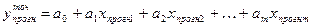. (3.14)

Если прогноз осуществляется не для одного набора факторных переменных, а для некоторого ряда наборов, то ряд точечных прогнозов исследуемой переменной можно представить в виде вектора, и вычислять его удобнее с использованием операций с матрицами:

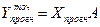, (3.15)

где

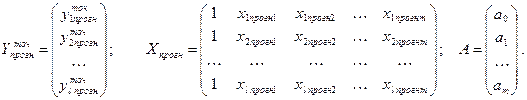(3.16)

Интервальный прогноз в рамках модели множественной регрессии строится с использованием соотношений, являющихся обобщением формул (2.22), (2.23), позволяющих строить прогноз на основе парной регрессионной модели.

Для нахождения размаха доверительного интервала необходимо вычислить матрицу V:

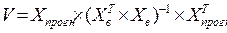. (3.17)

В выражении (3.17) участвуют матрица X_в, составленная из значений факторных переменных, имевших место в рядах наблюдений по правилу (3.5), и матрица X_прогн, составленная из прогнозируемых значений факторных переменных по правилу (3.16). Размерность матрицы V равна 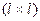, то есть зависит от числа прогнозируемых наборов факторных переменных. Если мы хотим рассчитать прогноз для одного набора факторных переменных, то получим матрицу V размером 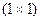, то есть число. Размах прогнозного интервала для i-го набора факторных переменных равен:

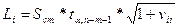. (3.18)

Величины 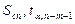вычисляются тем же образом, что и в (2.22), а 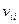является диагональным элементом матрицы (3.17). Тогда фактические значения исследуемой величины y для i-го набора значений факторных переменных с вероятностью (1-α) попадают в интервал:

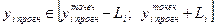. (3.19)

Несмотря на то, что в ходе исследования качества построенной нами модели (3.8) мы сделали вывод о нецелесообразности её использования для анализа и прогнозирования, рассчитаем прогноз для прогнозного значения температуры x1_прогн = 28 и величины торговой наценки x2_прогн = 25, то есть матрица X_прогн примет у нас вид вектора:

.

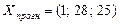Точечный прогноз будет тогда равен:

.

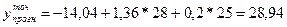Вычислим матрицу V по правилу (3.17), имея в виду, что матрицу 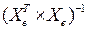мы уже вычислили в п.3.2, получим число (поскольку один прогнозируемый набор факторов): V=0,32. Далее, с учётом приведённых в п.3.3 стандартной ошибки 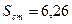и значения 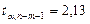, получим по формуле (3.18) размах интервала: L = 15,33. В итоге получим прогнозный интервал для фактического значения объёма продаж:

.

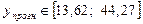Если мы сравним прогноз, полученный по двухфакторной линейной модели, с прогнозом, который мы сделали в п.2.8. на основе парной показательной модели, то увидим, что прогнозный интервал у двухфакторной модели больше, чем у однофакторной, то есть качество прогнозирования, несмотря на введение нового фактора, ухудшилось. Рекомендации о нецелесообразности использования, сделанные нами при исследовании качества линейной двухфакторной модели, оправдались.

Этот результат обусловлен, в первую очередь явно нелинейным характером связи между исследуемым объёмом продаж и основным фактором – температурой воздуха. Для улучшения парной показательной модели достаточно логично было бы ввести в модель дополнительную факторную переменную, не меняя показательной связи между объёмом продаж y и температурой воздуха x1. Это оказывается возможным с использованием техники вычислений, применявшейся нами при построении множественной линейной модели регрессии.

Построим по данным Примера 1 нелинейную модель вида:

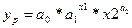. (3.20)

Применив операцию логарифмирования к уравнению (3.20) и сделав замены переменных, получим уравнение линейной модели множественной регрессии:

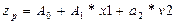, (3.21)

где 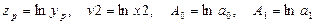. Соответственно, для нахождения коэффициентов линейной модели (3.21) 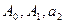, исследования свойств полученной модели и прогнозирования, будем использовать данные наблюдений из Таблицы 6, при этом каждое из значений в первом и третьем столбцах (данные для y и x2) необходимо предварительно прологарифмировать.

Применив процедуру МНК, получим модель:

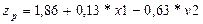. (3.22)

В соответствии с уравнением (3.22), в отличие от уравнения линейной модели (3.8), при увеличении торговой наценки объём продаж будет уменьшаться, что соответствует реальному процессу.

Произведя все операции для построения прогнозного интервала на основе линейной модели множественной регрессии, аналогично тому, как это описано выше, получим:

.

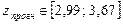Тогда с учётом соотношений 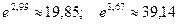прогнозный интервал для исходной исследуемой переменной с уровнем значимости α = 0,1:

.

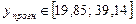С помощью построения нелинейной двухфакторной модели нам удалось уменьшить длину прогнозного интервала, полученного с помощью однофакторной показательной модели. Однако, интервал остаётся достаточно большим.

Если выбрать уровень значимости α = 0,3, то прогнозный интервал значительно уменьшится:

.

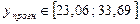При этом, однако, вероятность выполнения прогноза уменьшится с 90% до 70%.

В итоге наилучшей из построенных нами по данным Примера 1 моделей оказалась нелинейная двухфакторная модель вида:

.

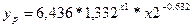Здесь использовано обратное преобразование коэффициентов: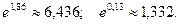

3.7. Применение обработки РЕГРЕССИЯ для определения параметров модели множественной линейной регрессии и её исследования

Построение и исследование модели множественной линейной регрессии является достаточно трудоёмкой процедурой. Трудоёмкость вычислений можно существенно снизить с помощью применения в MS Excel обработки Сервис/Анализ данных/РЕГРЕССИЯ.

Рассмотрим возможности использования обработки РЕГРЕССИЯ на данных примера из п.3.2. Данные для факторной переменной x3 мы использовать не будем, поскольку x3 была удалена из рассмотрения в результате проверки факторных переменных на мультиколлениарность. После вызова обработки РЕГРЕССИЯ зададим в соответствующих окнах диапазон ячеек, в которых находятся данные для Y вместе с заголовком столбца, диапазон ячеек, в которых находятся данные для факторных переменных x1, x2 также с заголовками столбцов, поставим флажок Метки (указывает, что в первой строке диапазонов стоят названия столбцов), зададим начальную ячейку для выходного интервала, поставим флажок Остатки. После выполнения обработки в ячейках, расположенных ниже и правее ячейки, указанной нами как начальная ячейка выходного интервала будут расположены результаты. Результаты обработки группируются в 4 таблицы. Если при вызове обработки мы дополнительно поставим флажок График остатков, то будут выданы графики остатков, по горизонтальной оси которых будут отложены значения одной из факторных переменных, а по вертикальной – значения ряда остатков ε_i. Число графиков будет совпадать с числом факторных переменных. Рассмотрим полученные результаты.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,9540
R-квадрат	0,9102
Нормированный R-квадрат	0,8653
Стандартная ошибка	6,2635
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		1590,289	795,144	20,268	0,008
Остаток		156,926	39,231
Итого		1747,214
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-14,042	6,284	-2,235	0,089	-31,489	3,404
X1	1,359	0,327	4,155	0,014	0,451	2,267
X2	0,197	0,316	0,624	0,566	-0,680	1,075
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	E отн
	-3,301	5,301	265,06
	3,494	0,006	0,17
	10,290	-5,290	105,79
	17,085	-5,085	42,38
	23,881	-1,881	8,55
	31,662	8,338	20,84
	43,390	-1,390	3,31

Во-первых, в колонке Коэффициенты третьей таблицы возьмём значения параметров множественной модели линейной регрессии. Уравнение модели имеет вид:

.

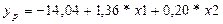В колонке t–статистика этой же таблицы находятся t-статистики для коэффициентов уравнения регрессии. Если возьмём при α=0,1 критическое значение t_кр(0,1; 7-2-1)=2,13, то получим, что модули первых двух параметров превышают критической значение, а модуль третьего параметра нет. Таким образом значения а₀=-14,04 и а₁=1,36 следует признать значимыми, а значение а₂=0,2 – незначимым. Следует отметить, что для определения значимости коэффициентов не обязательно определять критическое значение t-статистики. Достаточно сравнить соответствующие значение колонки P-Значение с выбранным уровнем значимости α и, если оно меньше чем α, то соответствующий параметр можно признать значимым. У нас получилось 0,089 < 0,1 и 0,014 < 0,1, то есть первые два параметра можно признать значимыми с вероятностью 90%, а 0,566 > 0,1, то есть третий параметр значимым не является, то есть наценку можно исключить из рассмотрения в рамках данной модели.

В первой таблице приведено значение коэффициента детерминации R-квадрат = 0,9102. Следовательно, можно сделать вывод, что в рамках линейной модели множественной регрессии изменение объёма продаж на 91% объясняется изменением температуры воздуха и торговой наценки.

В колонке F третьей таблицы приведено значение F-статистики Фишера равное 20,268. Для оценки значимости уравнения регрессии в целом сравним его с критическим значением F_кр(0,1; 2; 7-2-1) = 4,32. Поскольку F-статистика больше критического значения можно сделать вывод о значимости уравнения в целом. Этот же вывод можно сделать без определения критического значения F_кр путём сравнения значения из следующей колонки третьей таблицы Значимость F, равное 0,008, с выбранным уровнем значимости α = 0,1 (для возможности сделать вывод о значимости уравнения в целом это значение не должно превышать выбранный уровень значимости).

Для определения средней ошибки аппроксимации можно воспользоваться имеющимся в четвёртой таблице рядом остатков ε_i (колонка Остатки). Однако, потребуются дополнительные вычисления. Указанную таблицу следует дополнить колонкой 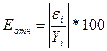, где Y_i – ряд наблюдений переменной Y (в учебных задачах задан в условии) и вычислить среднее значение для этой колонке. В результате получим:

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	E отн
	-3,301	5,301	265,06
	3,494	0,006	0,17
	10,290	-5,290	105,79
	17,085	-5,085	42,38
	23,881	-1,881	8,55
	31,662	8,338	20,84
	43,390	-1,390	3,31
			63,73	E отн.ср.

Модуль вычисляется с помощью функции ABS. Мы получили E отн.ср. = 63,73%, что значительно превышает 15%, следовательно, точность модели неудовлетворительная, и её не рекомендуется использовать для прогнозирования.

Заметим, что в первой таблице итоговых результатов имеется значение стандартной ошибки оценки, которое необходимо при построении интервального прогноза, а в последней четвёртой таблице имеется ряд расчётных значений исследуемого признака Ypi (колонка Предсказанное Y).