Определение комплексного числа.

Определение 1. Комплексным числом z называется выражение вида а + bi, (1)

где а и b – действительные числа, символ i удовлетворяет условию i² = - 1 .

Число а называется действительной частью комплексного числа, bi – мнимой частью, i – мнимой единицей.

Определение 2. Два комплексных числа z₁= a +bi и z₂ = c + di называются равными, если, соответственно, равны их действительные части и коэффициенты при мнимой единицы, т.е. a = c, b = d.

z = a + bi = 0 тогда и только тогда, когда a = 0 и b = 0, или, что тоже самое, когда a² + b² = 0.

Пример 1:Найдите действительные числа а и b из условия равенства двух комплексных чисел: - 2 + 5iа – 3ib = 9i + 2a – 4b.

Решение: Выделим в обеих частях равенства действительные и мнимые части данных комплексных чисел: - 2 + (5a – 3b)I = 2a – 4b + 9i

Используя правило равенства двух комплексных чисел, составим систему:

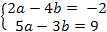
Решая данную систему, получим a = 3; b = 2.

Определение 3. Комплексные числа a + bi и a – bi называются комплексно – сопряжёнными.

Число, комплексно – сопряжённое числу z, обозначается через 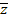. Так, если z = a + bi, то .

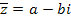Пример 2: Если z = - 2 + 4i, то .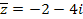

Квадратное уравнение ах² + вх + с = 0, для которого дискриминант D = b² – 4ac < 0 (1), в множестве действительных чисел не имеет решения, т. К. корень из отрицательного числа не имеет действительного значения. Однако в множестве комплексных чисел такое уравнение имеет два комплексно – сопряжённых решения:

x_1,2 = 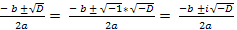, (2)

где – D = 4ac – b² > 0 (3), а поэтому 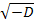есть некоторое действительное число.

Пример 3: Решите квадратное уравнение: 2х² – 6х + 9 = 0.

Решение: Используя формулы (2) и (3) находим корни уравнения: х_1,2 = =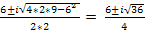

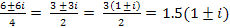
Ответ: х₁ = 1,5( 1 + i); х₂ = 1,5( 1 – i ).

Действия над комплексными числами.

1) Правило сложения: Суммой двух комплексных чисел является комплексное число равное сумме их действительных частей и мнимых частей, т. е. если z₁ = a₁ +b₁i, z₂ = a₂ + b₂i, то z₁ + z₂ = (a_{1 +} a₂) + (b₁ + b₂)i (3)

Пример 4:( 4 + 2i ) + (1 + 5i ) = ( 4 + 1 ) + ( 2 + 5 )I = 5 + 7i

В частности, если z = a + bi , 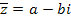, то z + 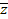= 2a. Следовательно, сумма комплексно – сопряжённых чисел есть действительное число.

2) Правило вычитания: Вычитание двух комплексных чисел определяется как операция, обратная сложению.Разностью комплексных чисел является комплексное число, равное сумме разности его действительных частей и разности мнимых частей, т. е.

z₁ – z₂ = (a₁ - a₂ ) + (b₁ – b₂)i. (4)

Пример5: (3 + 5i) – (6 + 3i) = (3 – 6) + (5 – 3)i = - 3 + 2i

3) Правило умножения:Произведением двух комплексных чисел z₁ = a₁ +b₁i, z₂ = a₂ + b₂i является комплексное число z₁z₂ = (a₁a₂ – b₁b₂) + (a₁b₂ + a₂b₁)i (5)

Пример 6:Найдите произведение комплексных чисел z₁ = (3 + 2i), z₂ = - 1 – i

Решение: Два комплексных числа можно умножать по правилу умножения многочленов при условии, что i² = - 1.

z₁z₂ = (3 + 2i)( - 1 – i) = - 3 – 3i – 2i – 2i² = - 3 – 5i – 2*( - 1) = - 1 – 5i

4) Правило деления:Частное от деления комплексного числа z₁ = a₁ +b₁i на комплексное число z₂ = a₂ + b₂i является комплексное число

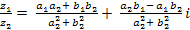(6)

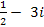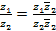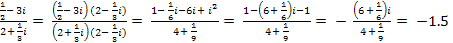Пример 7:Найдите частное от деления комплексного числа z₁ = на число z₂ = 2 + i. Решение: Частное от деления двух комплексных чисел, можно получить путём умножения числителя и знаменателя дроби на число, комплексно – сопряжённое знаменателю, т.е. = i