Применение понятия производной в экономике
Экономический смысл производной рассматривается на примере производственной функции. Производственной называют функцию, устанавливающую зависимость объёма выпускаемой продукции Q от величины затрат х: Q=f(x).
Производная данной функции показывает, насколько измениться объём выпуска продукции при увеличении затрат на единицу, т.е. эффективность затрат.
Если зависимость между издержками производства и объёмом выпускаемой продукции х выражается функцией 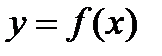 , то средние издержки при объёме продукции х выражается отношением
, то средние издержки при объёме продукции х выражается отношением 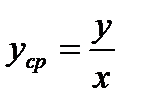 и функция предельных издержек выражается производной
и функция предельных издержек выражается производной 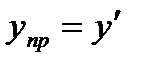
Эластичность издержек у относительно объёма выпускаемой продукции х рассчитывается по формуле:
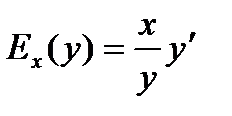 .
.
Пример 5.3.Зависимость между издержками производства и объёмом выпускаемой продукции х выражается функцией 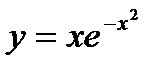 . Требуется:
. Требуется:
1) определить средние и предельные издержки при объёме продукции х=0,5 условных единиц;
2) найти эластичность издержек при выпуске продукции, равном х1=1 условных единиц.
Решение
1) Функция средних издержек выражается отношением 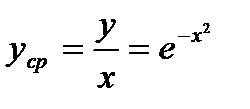 .
.
При х=0,5 средние издержки равны 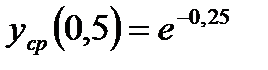 .
.
Функция предельных издержек выражается производной
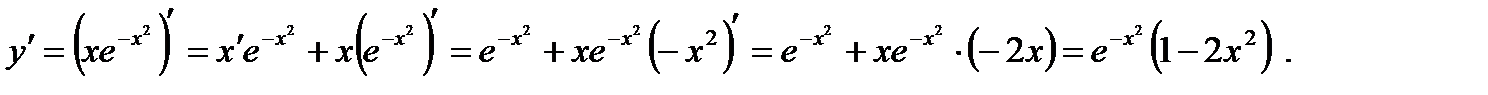
При х=0,5 предельные издержки составят
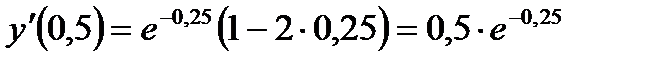 , что вдвое меньше средних издержек.
, что вдвое меньше средних издержек.
2) Эластичность издержек у относительно объёма выпускаемой продукции х рассчитывается по формуле:
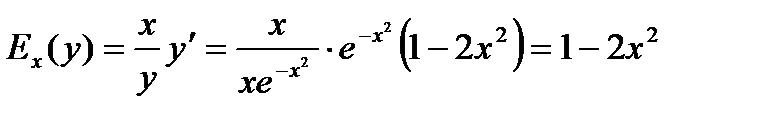 .
.
При х1=1, 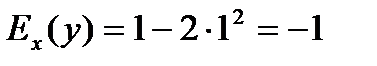 . Это означает, что при увеличении количества произведённой продукции на 1% издержки уменьшаться на 1%.
. Это означает, что при увеличении количества произведённой продукции на 1% издержки уменьшаться на 1%.
Если 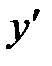 есть производная от функции
есть производная от функции 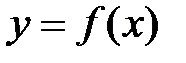 , то производная от
, то производная от 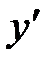 называется второй производной, или производной второго порядка и обозначается
называется второй производной, или производной второго порядка и обозначается 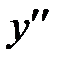 , или
, или 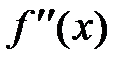 , или
, или 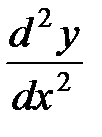 .
.
Аналогично определяются производные любого порядка:производная третьего порядка 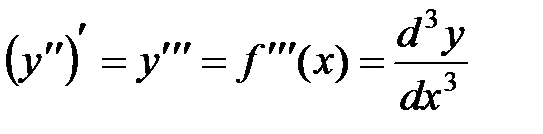 ; производная n-го порядка:
; производная n-го порядка:
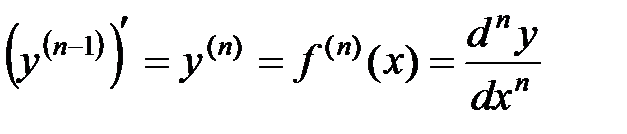 .
.
Функции многих переменных
Функция. определенная на некотором множестве Х арифметического п-мерного пространства, называется функцией п аргументов.
Будем говорить, что заданафункция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f(x,y) и называется значением функции f в точке (x,y).
Частной производной по переменнойх функции 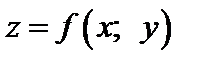 в точке
в точке 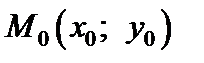 называется предел
называется предел
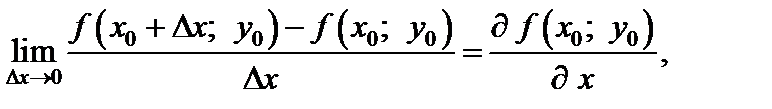 (5.1)
(5.1)
если он существует.
Производную (5.1) обозначают также 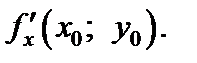
Частной производной по переменной у функции 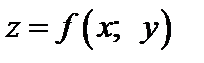 в точке
в точке 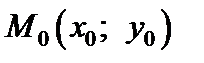 называется предел
называется предел
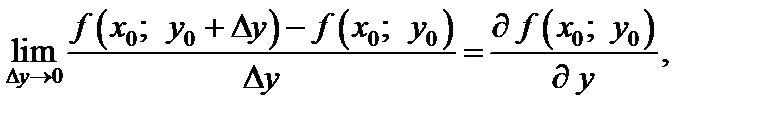 (5.2)
(5.2)
если он существует.
Производную (5.2) обозначают также 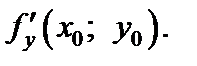
Для функции трех переменных 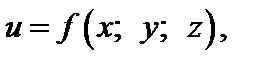 в случае их существования, аналогично определяют три частные производные
в случае их существования, аналогично определяют три частные производные 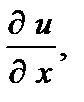
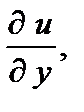
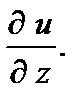
Дифференциал функции двух переменных 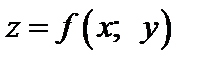 вычисляется по формуле
вычисляется по формуле 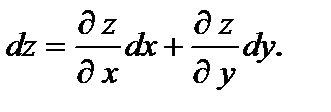
Пример 5.4. Вычислить 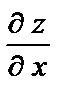 и
и 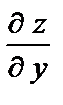 функции
функции
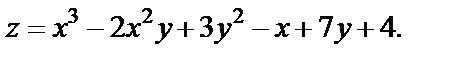 Найти значения частных производных в точке (–1, 1).
Найти значения частных производных в точке (–1, 1).
Решение Зафиксируем у, вычислим производную по х, пользуясь правилами дифференцирования (условно считаем y = const):
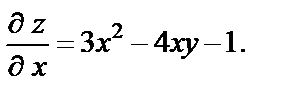
Тогда 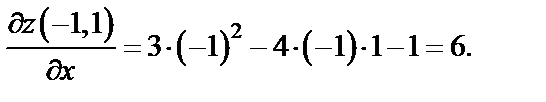
Зафиксируем х, вычислим производную по у: 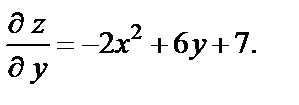
Тогда 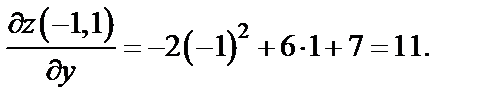
Пример 5.5. Найти dz функции 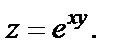
РешениеНайдем частные производные:
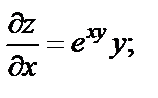
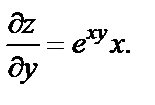
Тогда
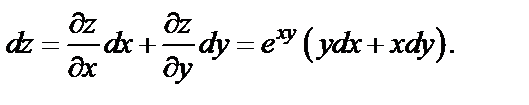
Контрольные вопросы
1. Что называется производной функции?
2. В чем состоит физический и геометрический смыслы производной?
3. Как находится производная суммы, произведения, частного двух
функций?
4. Какая функция называется сложной?
5. Как дифференцируется сложная функция?
6. Как записывается уравнение касательной к графику функции?
7. Как найти наименьшее и наибольшее значения функции на отрезке?
8. Сформулируйте правило Лопиталя.
9. Как вычисляются производные высших порядков?
10. Как найти интервалы монотонности функции?
11. Как исследовать функцию на выпуклость и как найти точки перегиба графика функции?
12. Какая функция называется функцией нескольких переменных?
13. Что такое частные производные?
14. Формула полного дифференциала функции.
