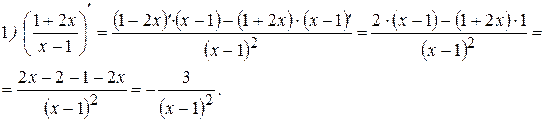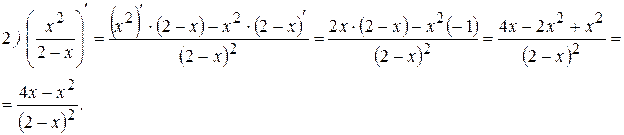III Непрерывность дифференцируемой функции

Установим необходимое условие существования производной.

Теорема:

Если функция 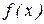имеет производную в точке 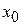, то она непрерывна в этой точке.

Доказательство: Любому значению 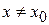, взятому из области определения функции 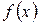, соответствует приращение аргумента 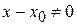и некоторое приращение функции 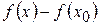. Рассмотрим тождество:

.

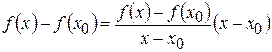Переходя к пределу при 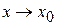в этом тождестве, получаем:

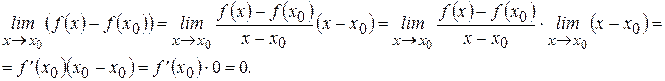Следовательно, 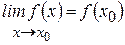, что и означает непрерывность функции 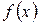в .

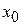Замечание: Из доказанной теоремы следует, что если функция не является непрерывной в некоторой точке, то она в этой точке не имеет производной, то есть непрерывность в точке – необходимое условие дифференцируемости в точке. Однако, следует заметить, что непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, то есть из непрерывности функции в точке не следует ее дифференцируемость в этой точке.

Пример: Функция 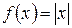непрерывна в любой точке числовой оси, в том числе и в точке 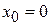(рис. 3)

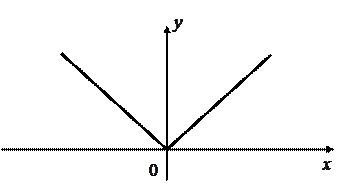
Рис. 3

Однако в точке 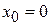данная функция не имеет производной. В самом деле: 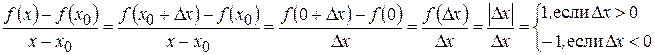Отсюда следует, что предел 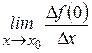не существует (так как, если предел существует, то только один) и, следовательно, не существует производной функции 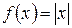в точке .

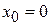Таким образом, существует функции, всюду непрерывные, но не имеющие производных в некоторых точках.

Производная суммы, разности, произведения и частного функций

Теорема 1

Если функци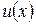и и 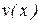имеют производные во всех точках интервала 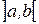, то производная их алгебраической суммы равна алгебраической сумме производных, то есть 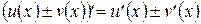для любого .

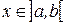Доказательство: рассмотрим функцию 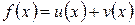, где 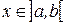и найдем производную этой функции, исходя из определения. Пусть 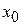– некоторая точка интервала 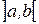. Тогда

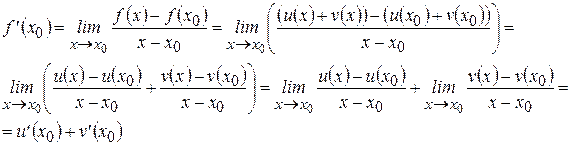
Итак, .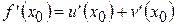

Так как 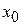– произвольная точка интервала 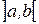, то имеем

.

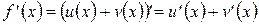Случай разности рассматривается аналогично. Теорема доказана.

Примеры: Найти производную:

1) ;

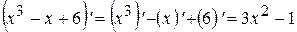2) ;

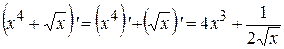Замечание: Данная теорема справедлива для любого числа слагаемых.

Теорема 2

Если функции 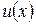и и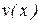меют производные во всех точках интервала 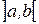, то 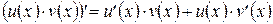для любого .

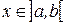Доказательство: рассмотрим функцию 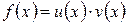, где 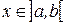и найдем производную этой функции, с помощью определения. Пусть 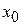– произвольная точка интервала 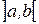. Тогда

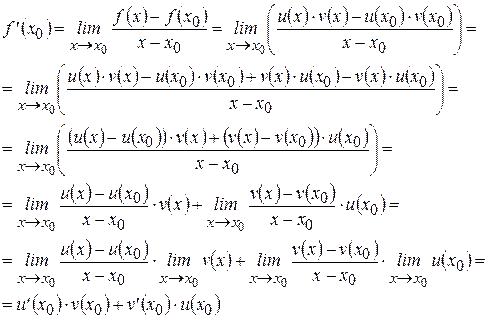
Итак, .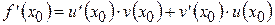

Так как 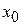– произвольная точка интервала 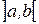, то имеем

.

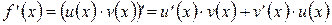Примеры:

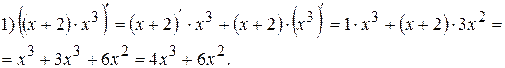
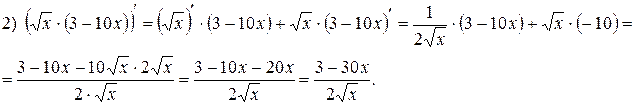
Следствие:Постоянный множитель можно выносить за знак производной:

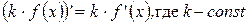
Доказательство:Применим теорему о производной произведения:

.

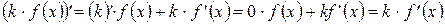Примеры:

;

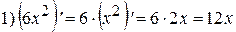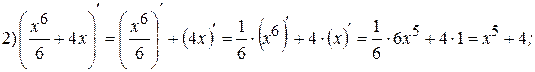
Теорема 3:

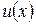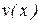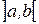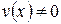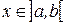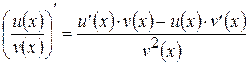Если функции и имеют производные во всех точках интервала , причем для любого , то для любого .

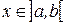Доказательство: Рассмотрим функцию 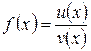, где 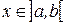и найдем ее производную, пользуясь определением. Пусть 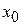– произвольная точка интервала 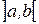. Тогда

.

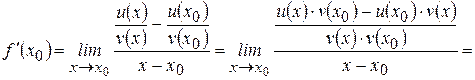
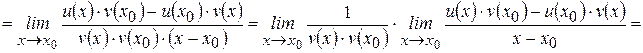
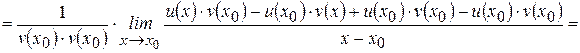
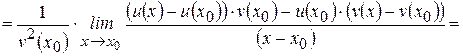
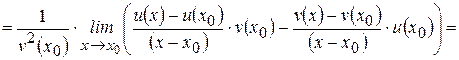
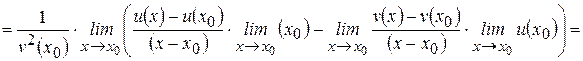
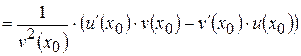Следовательно,

.

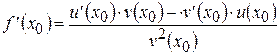А так как 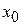– произвольная точка интервала 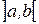, то имеем .

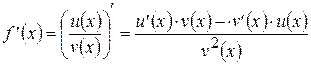Примеры: