Выбор состава множеств распознающих параметров
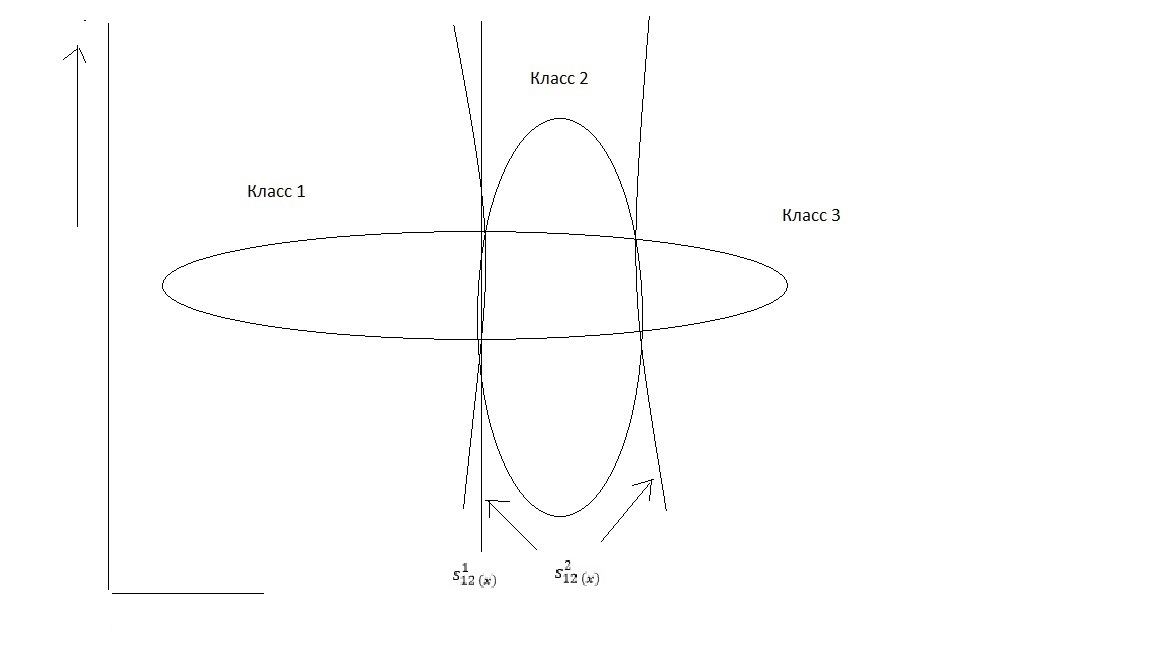
Принято считать неточность и неопределенность статистическими, случайными характеристиками и учитывать их при помощи методов теории вероятностей. Однако в реальных ситуациях источником неточности становятся помимо случайных величин, также и принципиальная невозможность оперировать точными данными из-за сложности системы, процессов, неточности, размытости ограничений, критериев и целей. Поэтому в задачах управления появляются классы объектов, не имеющие четких интервалов и границ в силу своей размытости (рис.3.10). Нечеткость таких классов выражается тем, что элемент системы может не только принадлежать или не принадлежать некоторому классу, но возможны также и промежуточные степени принадлежности, особенно характерные для нестационарных режимов у турбин энергоустановок.
3.3.1. Методы группирования данных, классификации и кластеров
Статистический подход к распознаванию образов можно использовать в тех случаях, когда имеющихся сведений недостаточно для описания образов или классов, которые, возможно, содержатсяв в рассматриваемом наборе данных. В таких обстоятельствах выходом из положения может оказаться применение статистических методов для анализа, что позволяет использовать всю имеющуюся априорную информацию. Но иногда необходимо провести и проанализировать новые наблюдения, что оказывается чрезвычайно затруднительным. Поэтому рекомендуется воспользоваться многошаговой роцедурой, при реализации которой попеременно используются статистический, «физический» и эвристический подходы.
Исходным материалом для применения статистической процедуры служит некоторый набор объектов, каждый из которых задается некоторым набором значений признаков. Далее, необходимо подготовить априорные сведения касающиеся возможных плотностей распределения значений признаков, адекватности признаков и т.д. При статистическом подходе совершенно безразлично, являются ли объекты распознавания реальными физическими объктами либо такими «нефизическими» категориями, как «социальное поведение» или «экономический прогресс», если все они допускают единообразное представление через признаки.
Рассмотрим следующие методы анализа данных:
1) Дискриминантный анализ: строятся функции, зависящие от признаков и обеспечивающие оптимальное в некотором смысле разделение объектов, относящихся к разным классам.
2) Выделение и выбор признаков: из некоторого (избыточного) набора признаков выбирается подмножество «наилучших» признаков или их комбинаций.
3) Кластерный анализ: данные разделяются на группы объектов, подобных в том или ином отношении.
4) Нечеткие методы.
Кроме того, некоторое внимание необходимо уделить проблемам, связанным с объемом выборки и числом признаков.
1. Дискриминантный анализ. Формирование дискриминантной функции, разделяющей два или несколько классов объектов, основывается на одном из следующих методов:
а) Статистические методы основываются главным образом на минимизации оценки ошибки классификации. Эта ошибка ( 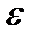 ) представляет собой вероятность неправильной классификации поступившего на распознавание произвольного
) представляет собой вероятность неправильной классификации поступившего на распознавание произвольного 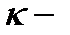 мерного объекта
мерного объекта 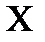 :
:
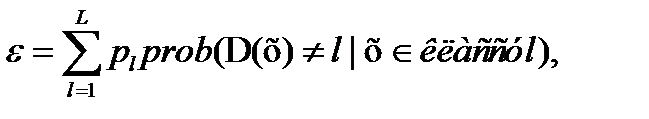 (1 3.32)
(1 3.32)
где L-число классов; 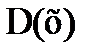 -функция, выносящая классификационное решение (может принимать одно из значений 1,2,…, l,…,L), и
-функция, выносящая классификационное решение (может принимать одно из значений 1,2,…, l,…,L), и 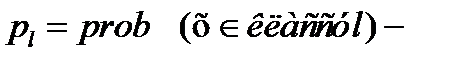 априорная вероятность принадлежности произвольного объекта
априорная вероятность принадлежности произвольного объекта  классу
классу  .
.
( 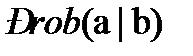 обозначает вероятность совершения события
обозначает вероятность совершения события  при выполнении условия
при выполнении условия  ).
).
Иногда минимизируются ожидаемые потери
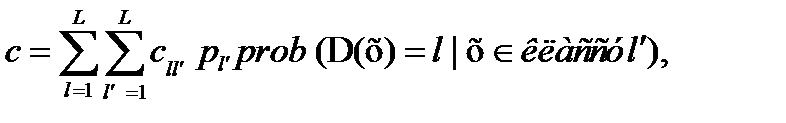 (2 3.33)
(2 3.33)
где 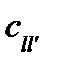 -потери, связанные с отнесением объекта
-потери, связанные с отнесением объекта 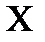 к классу
к классу 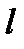 в то время, как на самом деле
в то время, как на самом деле 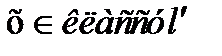 .
.
Если 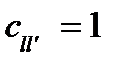 при
при 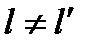 и
и 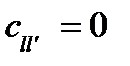 при
при 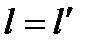 , то выражение
, то выражение
(2 3.33) совпадает с (1 3.32).
Воспользуемся критерием (1 3.32). Можно доказать, что значение (13.32) достигает минимума, если
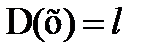 и
и 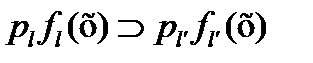 для любых
для любых 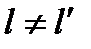 , (3 3.34
, (3 3.34
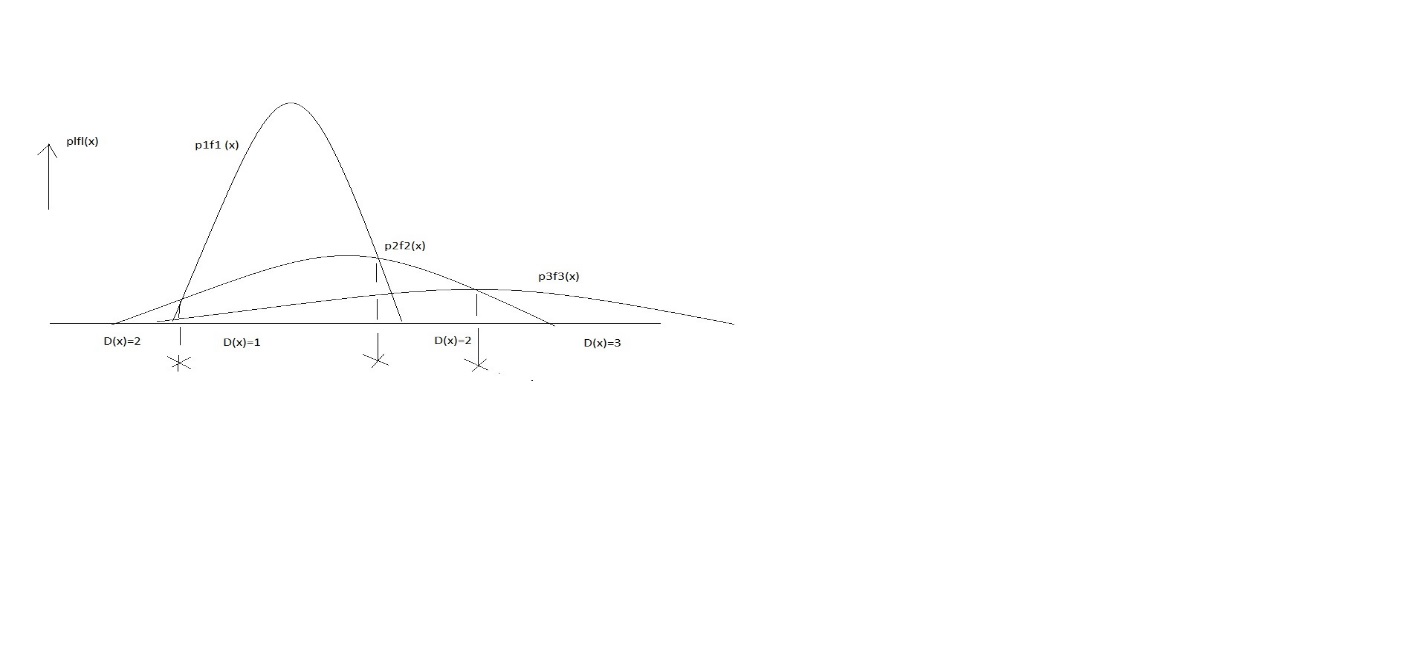
Рис.3.12 1. Пример применения правила классификации вида (3 3.34)
для случая одного признака ( 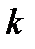 =1) и трех классов (
=1) и трех классов ( 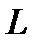 =3). Каждая
=3). Каждая
точка 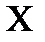 рисунка относится к тому классу, для которого произведение
рисунка относится к тому классу, для которого произведение
априорной вероятности на плотность распределения 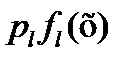
максимально.
Здесь 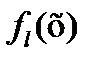 - плотность распределения класса
- плотность распределения класса 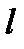 в
в 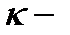 мерном признаковом пространстве. Правило классификации (3 3.34) называется бейесовским.
мерном признаковом пространстве. Правило классификации (3 3.34) называется бейесовским.
На рис. 3.12 1. представлен одномерный пример для случая трех классов ( 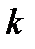 =1,
=1, 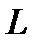 =3).
=3).
Точки 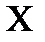 относятся к тому классу, которому соответствует максимальное значение
относятся к тому классу, которому соответствует максимальное значение 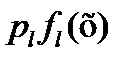 ; классификационные решения выносятся в соответствии с правилом (3 3.34).
; классификационные решения выносятся в соответствии с правилом (3 3.34).
При решении реальных задач сведения об априорных вероятностях и плотностях распределения приходится извлекать из имеющихся исходных данных.
Опишем ниже некоторые из методов, основанных на различных способах оценивания плотности распределения. Но при этом оценивание априорных вероятностей мы не будем выполнять, так как это чисто вычислительная задача.
б) Эвристические методы. Как известно в пракически применяемых методах не используется описанный принцип минимизации ошибки, основанный на оценках плотностей распределения. В этих методах заложены другие критерии, непосредственно связанные с имеющимися исходными данными; требуется меньше априорной информации о плотности распределения (т.е. о его нормальности), или имеется возможность использовать другие априорные сведения.
Рассмотрим процедуры классификации отличающиеся друг от друга требуемыми априорными сведениями о классах, числом оцениваемых параметров и вычислительной сложностью.
(1) Разделение с помощью квадратичных функций на основе использования плотностей нормального распределения.
Если все плотности распределений 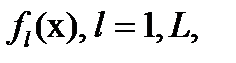 можно считать нормальными, то можно построить простую разделяющую функцию, обеспечивающую минимальную ошибку классификации. Плотность распределения определяется (при
можно считать нормальными, то можно построить простую разделяющую функцию, обеспечивающую минимальную ошибку классификации. Плотность распределения определяется (при 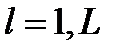 ) следующим выражением:
) следующим выражением:
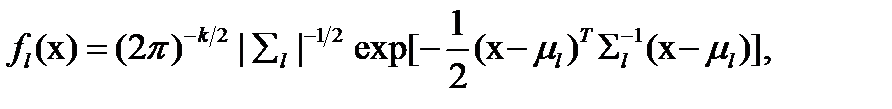 (4 3.35)
(4 3.35)
где 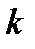 - число признаков;
- число признаков; 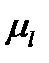 - среднее значение для класса
- среднее значение для класса 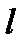 ;
;
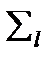 - ковариационная матрица класса
- ковариационная матрица класса 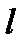 ;
;
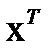 - результат транспонирования вектора
- результат транспонирования вектора 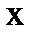 .
.
Можно убедиться в том, что 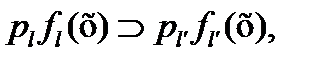 если
если
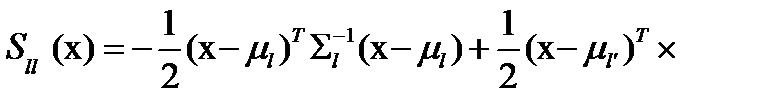
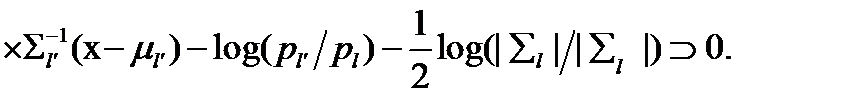 (5 3.36)
(5 3.36)
Таким образом, 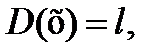 если
если 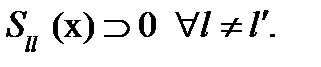 Здесь
Здесь 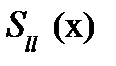 - квадратичная функция.
- квадратичная функция.
На рис.3.13 7 приведен пример разделения с помощью квадратичной функции для двух классов. Эта функция оптимальна, если истинные распределения нормальны. При решении реальных задач параметры 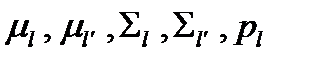 и
и 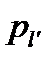 оцениваются по обучающему множеству.
оцениваются по обучающему множеству.
(2) Разделение с помощью линейных функций на основе использования плотностей нормального распределения.
Выражение (53.36) сводится к линейному виду если 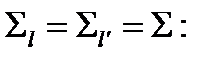
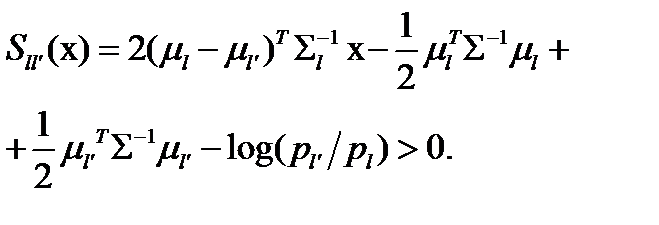 (6 3.37)
(6 3.37)
Это выражение называют линейной разделяющей функцией Фишера. При 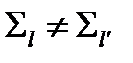 линеаризация достигается заменой
линеаризация достигается заменой 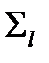 и
и 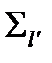 на
на
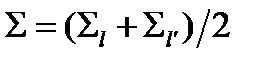 (см. рис. 3.13 7).
(см. рис. 3.13 7).
Рис. 3.13 7. Пример применения квадратичной разделяющей функции
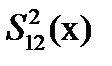 и ее линейного приближения
и ее линейного приближения 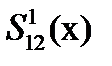 для случая двух классов.
для случая двух классов.
Линии равной плотности распределения приведены для двух
классов; предполагается, что 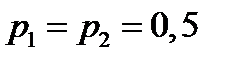 .
.
Известны и другие линейные разделяющие функции, основанные на
использовании плотности нормального распределения.
(3) Если вид кривой плотности распределения неизвестен и нельзя
сделать сколь бы то ни было обоснованных допущений о ее
характере, можно воспользоваться каким-либо
непараметрическим методом.
Используются парзеновские ядра оценок. Каждый объект в пространстве признаков заменяется «некоторым ядром», например плотностью нормального распределения с ковариационной матрицей 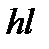 (l-единичная матрица). Могут быть использованы и ядра других типов. Оценка плотности распределения класса определяется теперь как среднее по обучающей выборке класса
(l-единичная матрица). Могут быть использованы и ядра других типов. Оценка плотности распределения класса определяется теперь как среднее по обучающей выборке класса
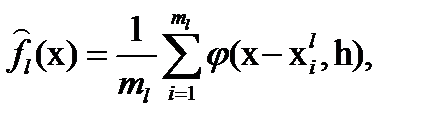 (7 3.38)
(7 3.38)
где 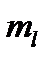 - число обучающих объектов
- число обучающих объектов 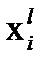 класса
класса 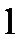 , а
, а 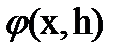 - ядро.
- ядро.
Оценка плотности распределения зависит от значения коэффициента сглаживания 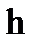 . Небольшие значения
. Небольшие значения 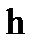 приводят к получению исключительно островершинных оценок, большие значения
приводят к получению исключительно островершинных оценок, большие значения 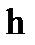 дают очень сглаженные оценки. Разделяющая функция
дают очень сглаженные оценки. Разделяющая функция
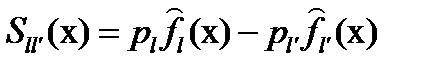 (83.39)
(83.39)
может в принципе быть нелинейной. Все обучающие объекты используются в процессе классификации предъявленного объекта 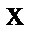 , причем процесс классификации может оказаться вычислительно неэффективным. Линейная аппроксимация разделяющей функции может быть эффективной.
, причем процесс классификации может оказаться вычислительно неэффективным. Линейная аппроксимация разделяющей функции может быть эффективной.
( 4) Правила ближайшего соседа.
Объект зачисляется в тот класс, которому принадлежит его ближайший сосед из обучающего множества (правило ближайшего соседа) или большинство из его 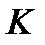 ближайших соседей (правило
ближайших соседей (правило 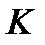 ближайших й). Этот метод имеет
ближайших й). Этот метод имеет
пределенный недостаток. При его использовании все обучающие объекты должны использоваться при получении каждого классификационного решения.
( 5) Оптимизация по какому-либо критерию ошибки.
Эвристический метод сводится к оптимизации параметров выбранной разделяющей функции (линейной, квадратичной или иного вида) по какому –либо критерию ошибки. Ддя этого можно использовать, например, число неправильно классифицированных объектов из обучающего множества, среднее или «взвешенное» расстояние между обучающим множеством и разделяющей функцией. Применение этого метода в сочетании с методом иерархического разделения, но методом одного контрольного объекта, может быть полезным.
( 6) Иерархическое разделение
Применение дерева решений весьма целесообразно, если число признаков велико. В каждой вершине дерева исследуется один из признаков и в зависимости от его значения выбирается очередная ветвь. Под конец в нижней вершине принимается классификационное решение. Подобные деревья являются очень гибким инструментом для использования априорных знаний. К сожалению, оптимальных схем обучения не существует.
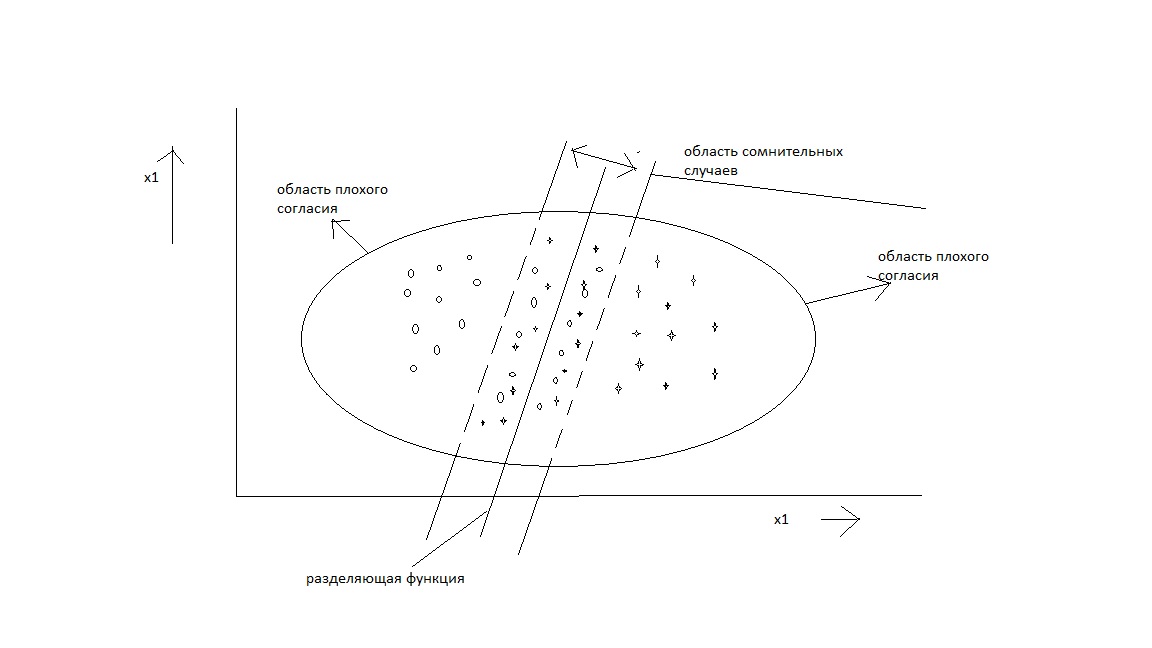
Рис. 3.14 8. Пример областей, соответствующих отказу от классификации,
для случая двух классов. Объект не классифицируется из-за сомнительности ситуации (область пересечения классов, близкая к границе, определяемой разделяющей функцией) или из-за плохого согласия (области со сравнительно низкой плотностью распределения).
( 7) Адаптивные разделяющие функции.
При решении некоторых прикладных задач приходится в процессе решения изменять разделяющую функцию, т.е. вносить небольшие изменения в значения ее параметров при неправильной классификации одного или нескольких объектов. Этой проблеме посвящено несколко работ.
Важным понятием дискриминантного анализа является «отказ от распознавания» (рис. 3.13 8).
3.3.2. РАЗМЫТОСТЬ ИНТЕРВАЛОВ, ОГРАНИЧЕНИЙ, КРИТЕРИЕВ И ЦЕЛЕЙ
