Нормировка функций в теории нечётких множеств

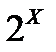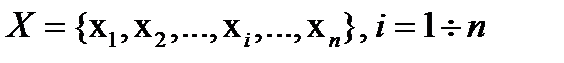В на определена и нормирована :

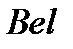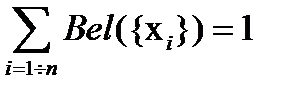. (1.24)

Опыт системных аналитиков говорит: использование только нормированных функций приводит к тривиальным результатам.

Для устранения тривиальности в теории нечётких множеств изначально заложена ненормированность функции принадлежности:

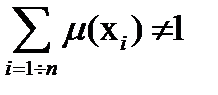(1.25)

Таким образом, в нечётких технологиях используется ненормированная входная функция 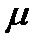, а внутренние (например, Bel) и выходные – нормированы.

Это позволяет учитывать все особенности и противоречия внешнего (физического) мира, а на выходе из технологии (дефаззификация) получать результаты в привычном диапазоне, например от 0 до 1, или в процентах.

Нечёткие отношения: прямая и обратная задачи

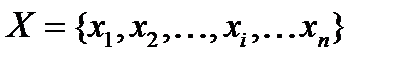В на определены нечёткие множества. 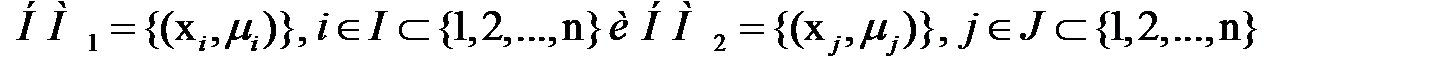, (1.26)

Аксиома 9:

Нечёткие отношения (НО) двух нечётких множеств есть совокупность упорядоченных пар {x_i, x_j} и соответствующих им значений функции принадлежности :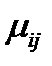

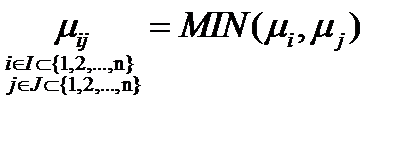. (1.27)

Нечёткое отношение между НМ₁ и НМ₂ есть частный случай использования композиционных правил нечёткого ввода НМ₁ => НМ₂.

Пусть имеется два набора факторов НМ₁= {(x_i, μ_i)}, где i равно от 1 до n, НМ₂= {x_j, μ_j}, где j равно от 1 до n и установлена зависимость между ними в виде правила: НМ₁ => НМ₂, которому соответствует нечёткое отношение {(x_i,x_j), (μ_i, μ_j)}. Теперь, если известен набор фактов НМ₁^’= {x_i^’, μ_i^’}, где i принадлежит от 1 до n, то можно сделать нечёткий вывод, что 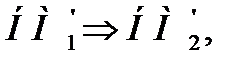или по 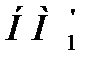определить 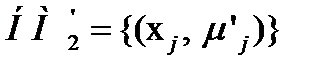, используя правило композиции:

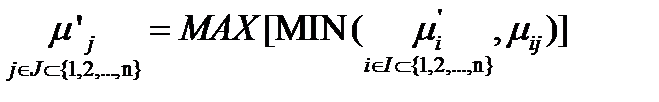(1.28)

перебором 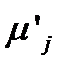, или методом С.Ю. Маслова, [25]. Приближённое решение

(в сторону уменьшения Bel):

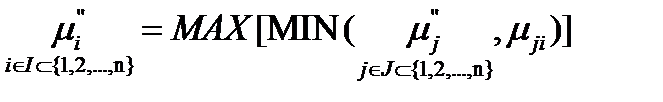, (1.29)

где μ_ji - матрица транспонирования относительно μ_ij.

Глава 2. Методы представления знаний с использованием

Приближенных и нечетких множеств

Нечеткие вычислительные технологии

Обобщенная схема нечетких технологий (НТ) есть преобразование:

Данные Знания

Результаты измерений по шкалам {1, 2, 3, 4}: 1. Шкала отношений – то есть измерений с истинным нулём (например, температура в градусах Кельвина (У. Томсона) [26], вес, длина, время и т.д.) 2. Шкала интервалов – измерение температуры в градусах Цельсия А. [26], или Фаренгейта Д. Г. [26], и аналогичные им с постоянными интервалами; 3. Порядковая шкала (ранговая) – измерения с градациями по объективному признаку, например, оценивание объекта; 4. Шкала номиналов – измерения с градациями по некоторой классификации (например, пол, возраст, профессия и т.д.).

Результаты расчётов (косвенных измерений) со свойствами {1,2}: 1. Связность – реализация взаимосвязей нескольких параметров (например, закон Ома Г. U= R*I) [26]; 2. Активность – возможность получения новых знаний (наприме6р, закон Ома Г. при U=0 – тепловые токи и при I=Imax – насыщение по току).

Такое преобразование использует материальный аппарат теории нечетких множеств и минимальную технологию, состоящую из следующих фрагментов:

· семантика объекта,

· создание базы знаний,

· распознавание объектов,

· управление процессом.