Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.

Под углом между векторами мы понимаем угол между векторами, равными данным и имеющим общее начало. Если нет ни каких указаний, то углом между векторами считается тот, который меньше .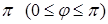

Скалярным произведением двух не нулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

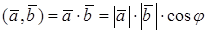
Признак перпендикулярности векторов: скалярное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны

.

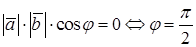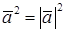т.к.

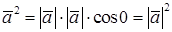
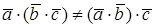
Скалярное произведение может быть вычислено, если известны координаты веторов: 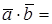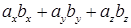. Скалярное произведение равно сумме произведений одноименных координат.

С помощью скалярного произведения вычисляют угол между векторами .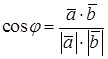

Упорядоченная тройка некомпланарных векторов называется право ориентированной или правой тройкой векторов, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противоположном случае тройка называется левой.

Пусть даны векторы 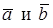. Построим вектор 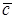, удовлетворяющий условиям:

a) ;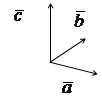

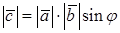b) ;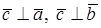

c) 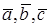образуют правую тройку векторов.

Вектор 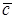называется векторным произведением

векторов . .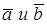

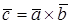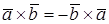антикоммутативность (следует из определения)

Геометрический смысл векторного произведения: 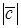- численно равен площади параллелограмма, построенного на векторах .

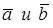Векторное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны.

,

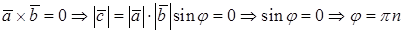т.е. векторы коллинеарны.

Смешанное произведение векторов.

Число 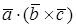называется смешанным произведением векторов 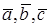иобозначается .

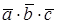Геометрический смысл: смешанное произведение не компланарных векторов равно по модулю объему параллелепипеда построенных на этих векторах. Смешанное произведение положительно, если векторы образуют правую тройку векторов, и отрицательно, если векторы образуют левую тройку векторов.

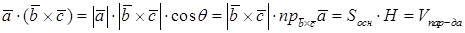
Знак смешанного произведения совпадает со знаком 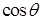. Если векторы 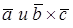лежат по одну сторону плоскости 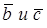, то 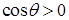и тройка векторов – правая; если векторы 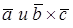лежат по разные стороны плоскости 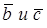, то 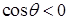и ройка векторов – левая.

Смешанное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы компланарны.

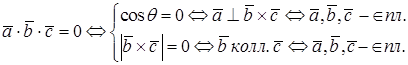
При перестановке множителей в смешанном произведении абсолютная величина числа не меняется, быть может, изменится, только знак

Смешенное произведение векторов равно определителю третьего порядка, составленному из координат векторов.

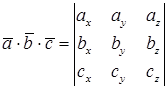
Плоскость в пространстве.

В прямоугольной декартовой системе координат каждая плоскость может быть задана линейным уравнением вида: 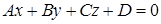, которое называется «общее уравнение»

Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору, имеет вид .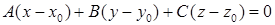

Геометрический смысл коэффициентов при неизвестных уравнения общего уравнения плоскости – координаты нормального вектора плоскости.

Если плоскость проходит через заданную точку 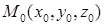компланарно двум векторам 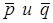, то уравнение плоскости можно написать так: 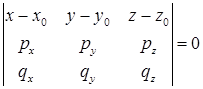, раскрывая определитель, получим уравнение плоскости.

Если плоскость проходит через три заданные точки 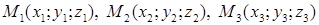, то уравнение плоскости получим из условия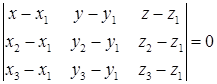

Если плоскость отрезает на координатных осях не нулевые отрезки т.е. пересекает координатные оси в точках 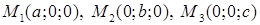, то получим уравнение плоскости в отрезках

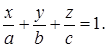
Расстояние от точки 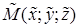до плоскости 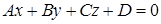можно вычислить по формуле

.

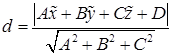Пусть даны две плоскост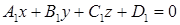и и .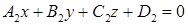

а) если плоскости пересекаются, то их нормальные векторы 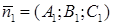и 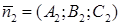не коллинеарны, т.е. 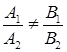или .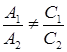

б) если плоскости параллельны (но не совпадают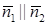), то , то

.

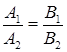
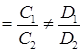в) если плоскости совпадают, то .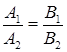

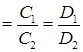Прямая в пространстве.

В прямоугольной декартовой системе координат

Каждая прямая может быть задана, как линия пересечения двух непараллельных плоскостей

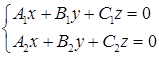
Верно обратное утверждение: каждое уравнение указанного вида при 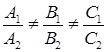определяет прямую в пространстве.

Однако более удобно при решении задач использовать другие уравнения.

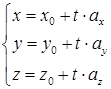– параметрическое уравнение прямой или

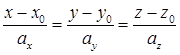– каноническое уравнение прямой (два линейно независимых уравнения), где 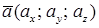– направляющий вектор прямой, а точка 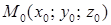принадлежит прямой.

Через две заданные точки M₁(x₁; y₁; z₁), M₂(x₂; y₂; z₂) можно провести прямую, уравнение которой находится по формуле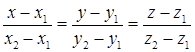

Пусть даны уравнения двух прямых.

L₁: 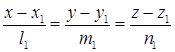L₂: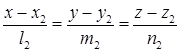

а) прямые скрещиваются (не лежат в одной плоскости), если выполняется условие

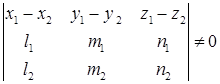
б) прямые пересекаются есл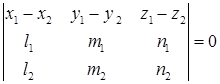и

и .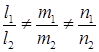

в) прямые параллельны если

, .

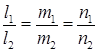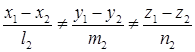г) прямые совпадают три вектора 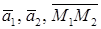коллинеарны.

Углом между двумя прямыми называется любой из двух углов между двумя параллельными им прямыми, проходящими через произвольную точку пространства. Вычислить косинус угла можно вычислить по формуле

.

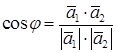Пусть дана прямая 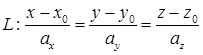и плоскость

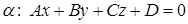
а) плоскость и прямая пересекаются если .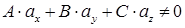

б) плоскость и прямая параллельны если

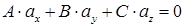, но .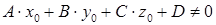

в) прямая лежит в плоскости есл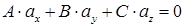и.

и .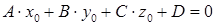

Углом между прямой и плоскостью называется, меньший из двух углов между этой прямой и ее ортогональной проекцией на эту плоскость.

.

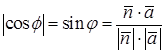Прямая и плоскость перпендикулярны, если 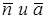коллинеарны.

Для того чтобы найти точку пересечения прямой и плоскости.

Воспользуемся параметрическим уравнением прямой и составим систему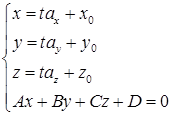

Если 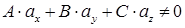, то система имеет единственное решение, а значит общая точка находится однозначно.

Прямая на плоскости.

Любая прямая на плоскости может быть задана линейным уравнением .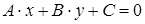

Верно и обратное утверждение: любое линейное уравнение определяет некоторую прямую.

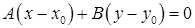– уравнениепрямой проходящей через заданную точку 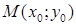перпендикулярно заданному вектору .

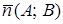Пусть 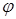- угол, который прямая L образует с положительным направлением оси ox. Тогда уравнение прямой можно записать в виде: 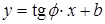или 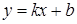, где k называется угловым коэффициентом, а b начальной ординатой. Если выразить y из общего уравнения, то получим равенство: 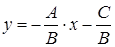. Таким образом,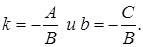

Пусть точка M₀(x₀; y₀) принадлежит прямой L, уравнение которой 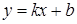, т.е. y₀ = kx₀ + b и y – y₀ = k(x –x₀) – уравнение прямой, проходящей через заданную точку в заданном направлении.

Пусть прямая L проходит через точку M₀(x₀; y₀) параллельно заданному вектору 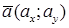– направляющему вектору данной прямой. Тогда

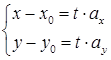– параметрическое уравнение,

а 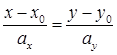– каноническое уравнение прямой.

Можно написать уравнение прямой проходящей через две заданные точки : .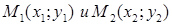

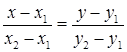Две прямые L₁ : 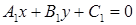и L₂ : 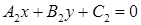на плоскости либо пересекаются, либо параллельны, либо совпадают.

В первом случае нормальные векторы 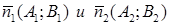не коллинеарны; т.е. 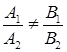или 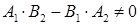. При этом условии система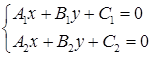

имеет единственное решение, так как главный определитель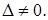

Если прямые L₁ и L₂ параллельны, то 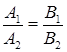и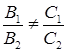

Если прямые L₁ и L₂ совпадают, то нетрудно видеть, что 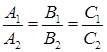и

Угол между двумя прямыми L₁ и L₂ определяется углом между их нормальными векторами : .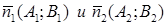

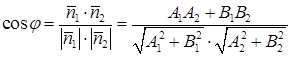Угол между двумя прямыми может быть найден с помощью угловых коэффициентов. Рассмотрим прямые L₁ 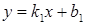и L₂ ,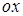

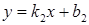которые составляют с координатной осью 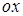углы .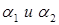

Если угол между прямыми L₁ и L₂ 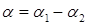, тогда 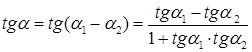, или .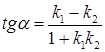

Если прямые параллельны, то 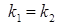– условие параллельности прямых.

Если прямые перпендикулярны, то 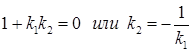– условие перпендикулярности векторов.

Пусть даны прямая L Ax + By + С = 0 и точка 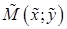не лежащая на данной прямой. Расстояние от точки до прямой можно вычислить по формуле .

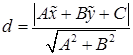Кривые второго порядка.

Общее уравнение кривой второго порядка имеет вид

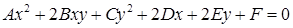
I. Эллипс.

Определение: Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2a, большее, чем расстояние 2c между фокусами.

Каноническое уравнение эллипса: .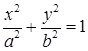

Число a называется большая полуось, b – малая полуось, причем .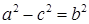

Из уравнения следует, что 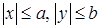, т.е. все точки эллипса лежат внутри прямоугольника .

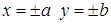Эллипс имеет центр симметрии – начало координат, и две оси симметрии – координатные оси. Если a = b, то уравнение принимает вид: 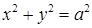. Т.е. окружность есть частный случай эллипса.

Отношение расстояния между фокусами 2c к длине большой полуоси 2a называется эксцентриситет и обозначается 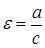. Т.к. 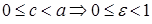; т.к. 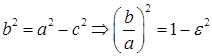т.е. эксцентриситет определяет форму эллипса.

II. Гипербола

Определение: Гиперболой называется множество точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2a, меньшее, чем расстояние 2c между фокусами.

Уравнение 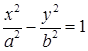называется каноническим уравнением гиперболы. Число a называется действительная полуось, а b – мнимая полуось, причем по определению .

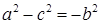Из уравнения (2) следует, что 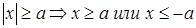. Ось ox пересекает гиперболу в двух точках A₁(–a; 0) и A₂(a; 0) и называется действительной осью гиперболы. Ось oy не пересекает гиперболу и называется мнимой осью. Две прямые 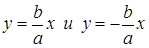являются асимптотами гиперболы.

Асимптоты гиперболы являются диагоналями прямоугольника со сторонами .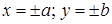

Отношение расстояния между фокусами 2c к действительной оси 2a называется эксцентриситетом гиперболы и обозначается 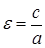. Т.к. 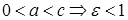, т.е. эксцентриситет определяет форму гиперболы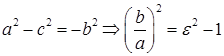

Уравнение 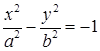определяет гиперболу сопряженную данной. У них меняются местами действительная и мнимая оси.

III. Парабола

Определение: Параболой называется множество точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директрисой.

Расстояние от фокуса параболы до ее директрисы называется параметром (p>0). Эксцентриситет параболы принимается равным единице .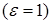

Каноническое уравнение параболы .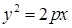

Ось ox является осью параболы, начало координат – вершиной, 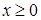уравнение директрисы .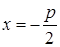