Кафедра физики горных пород и процессов
Кафедра физики горных пород и процессов
Допущено Учебно-методическим объединением
вузов Российской Федерации по образованию в области
горного дела в качестве учебного пособия для студентов
вузов, обучающихся по направлению подготовки
«Горное дело»
И. М. Шведов
Сборник задач и упражнений по гидромеханикЕ для практических
занятий и самостоятельной работы
Давление жидкости на плоские и криволинейные поверхности
ЧАСТЬ II

Москва 2008
УДК 532.5(075.8):622.5
Шведов И.М. Сборник задач и упражнений по гидромеханике для практических занятий и самостоятельной работы. - Учебное пособие.
Часть II. Давление жидкости на плоские и криволинейные поверхности, М.: МГГУ, 2008. – 102 с.
Рассмотрены основные понятия и положения гидромеханики раздела гидростатики – определение величины гидростатического давления на поверхности различной конфигурации. Приведены примеры расчета устойчивости плоских стенок и построения эпюр давления, определение величины полной силы гидростатического давления на криволинейные поверхности.
По каждому из разделов предложены задачи различной сложности для практических занятий и варианты заданий для самостоятельных работ. Приведены указания к решению задач и ответы для самопроверки.
Сборник содержит 163 практических заданий, из них 56 вариантов для самостоятельной работы, 92 задачи из раздела гидростатического давления на плоские и криволинейные поверхности, подробно разобраны решения 15 типовых задач.
Сборник рекомендован для студентов вузов, обучающихся по направлению подготовки «Горное дело».
Рецензенты:
Астрахан И.М., канд. физ.-мат. наук, профессор кафедры «Нефтегазовая и подземная гидромеханика» Российского государственного университета нефти и газа;
Бинги В.Н., докт. физ.-мат. наук, заведующий лабораторией Института общей физики РАН
© Московский государственный горный университет, 2008
© И.М.Шведов, 2008
Содержание
Введение………………………………………………………………….....6
ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ СТЕНКИ
4.1. Нахождение полной силы давления и центра давления………..……8
4.2. Построение эпюр давления……………..……………………...……...9
4.3. Примеры решения задач ………...…………………...………...…….14
4.4. Задачи для практических занятий ……………….…………...….…..28
4.5. Варианты заданий для самостоятельной работы……..………..…...47
4.6. Ответы, указания к решению задач …………..……………………..50
ДАВЛЕНИЕ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ
5.1. Нахождение полной силы давления, построение тела давления…..54
5.2. Примеры решения задач…………...………………...…………….....55
5.3. Задачи для практических занятий………..……………...……….…..64
5.4. Варианты заданий для самостоятельной работы……..….....………79
5.5. Ответы, указания к решению некоторых задач ……………….……82
ПРИЛОЖЕНИЕ Г. Координаты центра тяжести и момент инерции
некоторых плоских фигур ………………………………...……...……...85
ПРИЛОЖЕНИЕ Д. Координаты центра тяжести и моменты инерции
некоторых объемных фигур ………………………………/……….…….90
ПРИЛОЖЕНИЕ Е. Вычисления центра тяжести произвольных плоских и объёмных фигур…………………………………….………..................98
Список использованных источников……………………………..…….102
Условные обозначения
| ρ | - | плотность, кг/м3 |
| M, m | - | масса, кг |
| Ω, | - | объём, м3 |
| ω | - | площадь, м2 |
| γ | - | удельный вес, Н/м3 |
| G | - | вес (сила тяжести), Н |
| g | - | ускорение свободного падения, м/с2 |
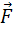 | - | сила механическая Ньютона , Н |
| D | - | диаметр внешний, м |
| d | - | диаметр внутренний, м |
| h | - | глубина (высота), м |
| L, l | - | длина, м |
| B,b | ширина, м | |
| HТ | глубина погружения центра тяжести, м | |
| pабс | - | давление полное (абсолютное), Па |
| po | - | давление внешнее, Па |
| pатм | - | давление атмосферное, Па |
| pизб | - | давление избыточное, Па |
| pман | - | давление манометрическое, Па |
| hp | - | высота пьезометрическая, м |
| LТ | - | координата центра тяжести, м |
| LД | - | координата центра давления, м |
| ε | - | эксцентриситет, м |
| J0 | центральный момент инерции площадки, м4 | |
| Mуд | - | момент удерживающий, Н·м |
| Mопр | - | момент опрокидывающий, Н·м |
| kуст | - | коэффициент устойчивости |
| R | - | полная сила гидростатического давления , Н |
| Rx(y) | - | горизонтальные составляющие полной силы давления, Н |
| Rz | - | вертикальная составляющая полной силы давления, Н |
| δ | - | толщина стенки трубы, м |
| σ | - | нормальные напряжения, Па |
Введение
Данный сборник часть II, является продолжением части I «Сборника задач и упражнений по гидромеханике для практических занятий и самостоятельной работы», содержит задачи по гидростатике, относящиеся к разделам “Давление жидкости на плоские стенки” и “Давление жидкости на криволинейные поверхности“.
В сборник включены апробированные задачи, предлагаемые на практических занятиях и контрольных работах для студентов, обучающихся по направлению «Горное дело», а также ряд оригинальных задач для самостоятельного решения, для углубления полученных знаний по курсу «Гидромеханика».
Выдержанный в единой структуре представления материала, каждый раздел сборника содержит необходимые минимальные теоретические сведения и рабочие формулы, касающиеся материала данного раздела, необходимые для повторения и закрепления пройденного лекционного материала, методические указания и примеры решения типовых задач
В трёх приложениях представлены материалы справочного характера, вполне достаточные для самостоятельного решения задач.
Наличие в сборнике обширного и разнообразного материала позволяет составить индивидуальное задание для каждого студента для самостоятельной и контрольной работы.
Методически, после ознакомления с соответствующим теоретическим материалом и указаниями по решению типовых задач, следует переходить к самостоятельному выполнению полученного задания.
В решениях задач константу ускорения свободного падения принять g = 9,81 кг/м2, плотность воды ρ = 1000 кг/м3 .
Свойства жидкостей и процессы определять (если в задаче не конкретизированы) при стандартных физических условиях (t = 20 0C, атмосферное давление р = 101,325 кПа = 760 мм рт. ст. = 10 м вод. ст.).
Учебное пособие подготовлено в полном соответствии с рядом разделов примерной программы учебной дисциплины ОПД Ф.02 « Механика. Курс «Гидромеханика» для студентов, обучающихся по направлению подготовки 130400 «Горное дело».
Построение эпюр давления
Эпюрой давления жидкости называется графическое изображение распределения изменения гидростатического давления жидкости по твёрдой поверхности, соприкасающейся с ней, и при ее построении учитывается только избыточное давление.
Эпюра давления в покоящейся жидкости изменяется пропорционально глубине залегания от поверхности согласно основному уравнению гидростатики:
р=р0+ρgh или р=ра+ρgh, (4.5 )
где ра - атмосферное давление на поверхности (или в общем виде р0 – внешнее давление над свободной поверхностью жидкости) будет постоянно для всей глубины. Избыточное давление ρgh изменяется по закону прямой линии и на поверхности будет равно нулю.
Если рассматриваемая жидкость – вода, то ρg= γ = 9810 Н/м3, тогда при глубине h1=1м избыточное давление равно ρg·h1=9810 Па (откладывается в задаваемом масштабе). Для глубины h2=2 м избыточное давление будет ρg·h2=9810·2 Па и т.д. Очевидно, прямая давления для воды будет наклонена под углом α=45°.(рис.4.2).
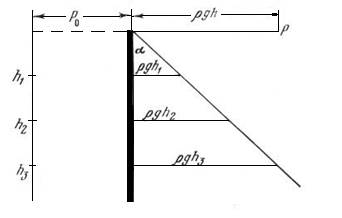
Рис.4.2. Эпюра гидростатического давления на вертикальную стенку
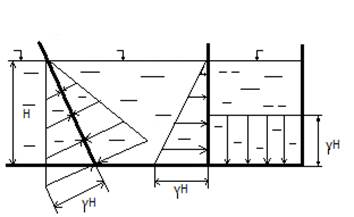
Эпюра давления строится со стороны жидкости. Стрелками на эпюре показывают направление действия давления (вернее, направление действия нормальных напряжений, возникающих от действия давления, т.к. согласно 2-му основному свойству гидростатическое давление скалярно). Размер стрелки (ордината) откладывается в масштабе и количественно соответствует величине давления. Пример построения эпюр давления на различные поверхности приведены на рис.4.3.
а)
б)
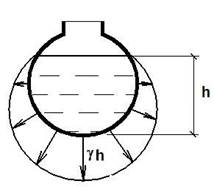
Рис.4.3. Пример построения эпюр давления на различные плоские (а), и криволинейные (б) поверхности
Для вертикально расположенной стенки, например АБГД, эпюрой давления является треугольник АКГ (рис.4.4). Пространственная эпюра давления на вертикальную стенку будет представлять собой треугольную призму, площадь основания которой равна ρgH2/2, а высота – ширине стенки В. Тогда объем призмы численно равен величине силы давления на данную прямоугольную стенку.
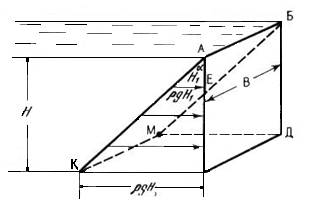
Рис.4.4. Эпюра гидростатического давления на вертикальную плоскую поверхность
Если стенка наклонена к горизонтальной плоскости под углом α, как показано на рис.4.5, то эпюром гидростатического давления является треугольник БАВ, с углом β=90° в точке В. Полная сила давления на стенку вычисляется по формуле:
R = ρgH2B/2sinα (4.6)
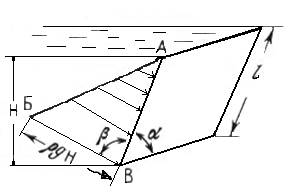
Рис.4.5 Эпюра гидростатического давления на наклонную плоскую поверхность
При действии жидкости на вертикальную стенку, например CNOP с двух сторон Н1 и Н2 (рис 4.6), необходимо построение эпюр давления с каждой стороны и нахождение результирующей эпюры полной силы давления. Так, эпюра давления с левой стороны стенки соответствует треугольнику ANC, с правой - треугольнику KCL.
Эпюрой общего давления будет трапеция MENC, полученная как разность эпюр ANC и KCL. Полная сила давления находится как разность давлений слева и справа:
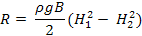 (4.7)
(4.7)
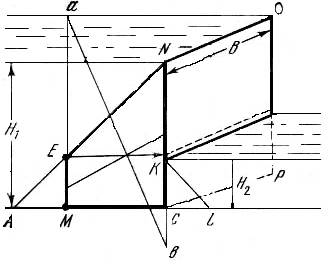
Рис.4.6 Построение обобщенной эпюры давления при двухстороннем действии жидкости
Эпюры давления служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: подпорных стенок бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
На практике в большинстве случаев строят эпюры только для избыточного (манометрического) давления. Атмосферное давление не учитывают из-за его взаимокомпенсации с той и другой стороны ограждающей конструкции.
Примеры решения задач
Пример 1. Прямоугольная подпорная стенка высотой H и шириной B испытывает гидростатическое давление воды глубиной h (рис.4.7). Плотность кладки стенки ρкл = 2500 кг/м3 .
Требуется выполнить:
1. Построить эпюру гидростатического давления.
2. Определить величину гидростатического давления (избыточного) на 1 погонный метр длины стенки.
3. Определить координату центра давления.
4. Определить Куст подпорной стенки на опрокидывание.
5. Вычислить ширину стенки В при запасе устойчивости kуст =3.
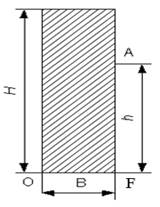
Рис.4.7
Решение. Для построения эпюры гидростатического давления на стенку определяем величину в точках А и В избыточного (манометрического) давление по формуле:
р изб = ρвgh ,
где h – глубина погружения данной точки под уровень воды, м., ρв - плотность воды, кг/м3.
При построении эпюры гидростатического давления следует помнить, что давление всегда направлено по нормали к площадке, на которую оно действует (рис.4.8).
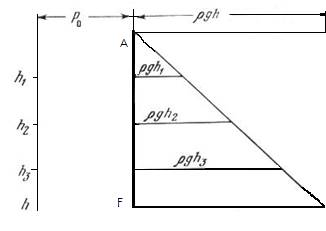
Рис.4.8
Величина полной силы избыточного гидростатического давления R на плоскую стенку вычисляется по формуле (4.1):
R = pтω,
где pт. – давление в центре тяжести смоченной поверхности, Па (Н/м2); ω – площадь смоченной поверхности, м2.
Точка приложения суммарной силы избыточного гидростатического давления D называется центром давления. Положение центра давления определяется по формуле (4.3) :
Lд = Lт + ε = Lт + J0/ Lт·ω ,
где Lд– расстояние на плоской стенке от центра давления до пьезометрической поверхности (в данном случае - свободного уровня жидкости), м; Lт – расстояние на плоской стенке от центра тяжести стенки до пьезометрической поверхности (в данном случае -свободного уровня жидкости), м;
ω – площадь смоченной поверхности, м;
J0– центральный момент инерции смоченной плоской площадки относительно горизонтальной оси, проходящей через центр тяжести. Для плоской прямоугольной фигуры:
J0 = L·h3/12 ,
где L- длина стенки ( в данной задаче L = 1 пог. м).
Удерживающий момент относительно точки О равен:
Муд = G·B/2 ,
где G – вес подпорной стенки, кН, G = Ω·ρкл , где Ω – объем стенки,
ρкл – плотность кладки.
Опрокидывающий момент равен:
Мопр = R·(h - Lд) .
Коэффициент устойчивости (запас устойчивости) на опрокидывание равен отношению удерживающего момента сил относительно точки О к опрокидывающему моменту:
kуст = Муд/ Мопр .
Если значение kустполучится меньше трех, то следует определить ширину стенки L, которая бы удовлетворяла запасу устойчивости kуст = 3 (полученное значение следует округлить до 5 сантиметров в большую сторону).
Пример 2. Определить величину R - равнодействующую гидростатического давления жидкости c gв = 10 кН/м3, и координату её приложения Lд на плоскую вертикальную стенку (рис.4.9). В одной части бака жидкость находится на уровне h1 = 2 м, в другой – на уровне
h2 = 1 м.
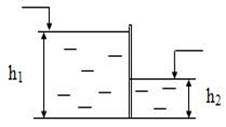
Рис.4.9
Решение. Гидростатическое давление воды на 1 погонный метр длины стенки равно:
с левой стороны R1 = gв h12/2 = 20 кН;
с правой стороны R2 = gв h22/2 = 5 кН.
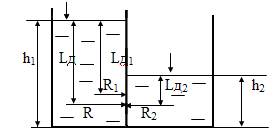
Рис.4.10
Следовательно, равнодействующая давления будет представлять алгебраическую сумму давлений R1 и R2, т.е. R = 20 - 5 = 15кН.
Точка приложения этой равнодействующей (рис.4.10) может быть найдена из уравнения моментов. Lд – расстояние от поверхности воды до центра давления на прямоугольную стенку: Lд1 = 2/3h1 и Lд2 = 2/3h2; Lд1 = 1,3 м и Lд2 = 0,67 м.
Уравнение моментов: М = М1 – М2 Þ R Lд = R1 Lд1 – R2 Lд2
½ gв (h12 – h22) Lд = 1/3 gв (h13 – h23) откуда Lд = 2(h13 – h23) /3(h12 – h22) = 1,56 м.
Ответ: R = 15 кН; Lд = 1,56 м.
Пример 3. В плоскодонной лодке с осадкой h1 = 2 м на дне находится вода на уровне h2 = 0,5 м. Угол наклона борта a = 600; объёмный вес воды gв = 9,81 кН/м3. Определить гидростатическое давление на борт лодки (на 1 погонный метр длины) и построить эпюру этого давления.
Решение. Гидростатическое давление воды на 1 пог.м длины борта лодки снаружи:
R1 = gв h12/2sina = 22,57 кН.
Гидростатическое давление воды на 1 пог.м длины лодки изнутри:
R2 = gв h22/2sina = 1,37 кН.
Равнодействующая гидростатического давления есть алгебраическая сумма давлений R1 и R2. Следовательно, R = R1 - R2 = 21,2 кН
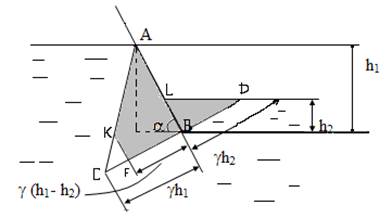
Рис.4.11
Для построения эпюры давления определяем величину гидростатического давления в точках А и В слева и точках L и В справа (рис.4.11). Откладываем в выбранном масштабе от данных точек полученные величины давлений, нормально к поверхности действия, и соединяем полученные вновь точки. Полученные треугольники АСВ и DBL есть эпюры давлений, соответственно, слева и справа на поверхность АВ. Результирующая эпюра давления на поверхность АВ равна разности ΔАВС – ΔDBL и представляет собой трапецию АКFB.
Ответ : R = 21,2 кН.
Пример 4. Для выпуска воды из резервуара у его дна устроен дисковый затвор А высотой а = 0,4 м и шириной b = 1,0 м (рис.4.12). Глубина воды в резервуаре Н = 4 м. Требуется определить силу, передающуюся на ось затвора и глубину погружения центра давления.
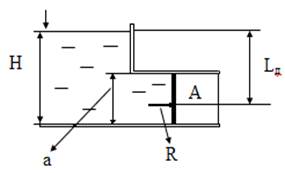
Рис.4.12
Решение. Сила давления жидкости, действующая на затвор равна:
R = w g Hт = а b gв (Н – а/2) = 14,92 кН,
где Нт – глубина погружения центра тяжести затвора, ω – площадь поверхности затвора.
Глубину погружения центра давления найдем по формуле (4.3):
Lд = Lт + J0/ w·Lт = Lт + J0/ w·Lт ,
где J0 - центральный момент инерции смоченной поверхности затвора (прямоугольник), Lт – координата центра тяжести прямоугольной поверхности затвора.
В данном случае координата L совпадающая с плоскостью стенки направлена вертикально вниз, и величина Lт будет совпадать со значением Hт.
Откуда глубина погружения центра давления LД ( или координата yд ,если направление оси y выбрано вертикально вниз) будет равно:
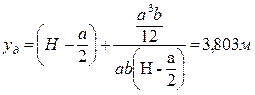
Ответ : R = 14,92 кН; Lд = 3,803 м.
Пример 5. В жидкости находится прямоугольная призма, размеры которой показаны на рис.4.13. Найти сумму сил, действующих на переднюю и нижнюю грани призмы, если давление жидкости равно
2·105 Па. Чему будет равна сумма сил, действующих на призму?
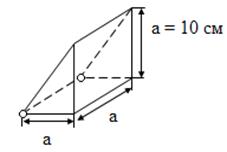
Рис.4.13
Решение. Сила гидростатического давления, действующая на поверхность призмы : F = p·ω (рис.4.14). Находим значения площадей поверхности ωн = ωn , ω3 и значения сил для правой Fn, нижней Fн и наклонной Fн поверхностей призмы:
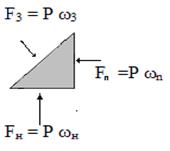
Рис.4.14
ωн = ωn = 0,1 . 0,1 = 0,01 м2;
Fн = Fn = 2 . 105 . 0,01 = 2000 H;
F1 = Fн . 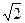 = 2000
= 2000 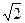 H (см.рис.4.15);
H (см.рис.4.15);
ω3 = (0,1 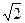 ) . 0,1 = 0,01
) . 0,1 = 0,01 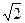 м2;
м2;
F3 = 2 . 105 . 0,01 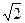 = 2000
= 2000 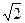 H.
H.
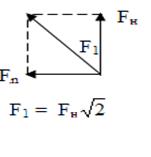
Рис.4.15
F3 уравновешивает F1; давления на боковые стенки также уравновешиваются Þ F2 = F3 = 0, поэтому сумма всех сил, действующий на призму, будет равна нулю (рис.4.16) :
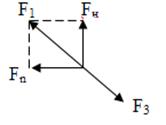
Рис.4.16
Ответ: F1 = 2000 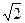 H; FΣ = 0
H; FΣ = 0
Пример 6. Результирующая сила, действующая со стороны сжатой жидкости на три грани правильного тетраэдра, равна F. Длина ребра тетраэдра равна а. Определить давление жидкости.
Решение. Из условия равновесия следует, что на 4-ую грань тетраэдра также действует сила F. Поскольку площадь 4-ой грани (как и всех остальных) равна ω = 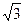 /4 . a2, то
/4 . a2, то
р = F/ω = 4F/ 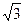 a2
a2
Ответ: р = 4F/ 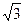 a2
a2
Пример 7. Бетонный куб с ребром 20 см погружен в воду (рис.4.17). Нижняя грань куба удалена от свободной поверхности воды, находящейся под внешним атмосферным давлении р0 = 1 ат, на глубину 1 м. Определить величину силы, действующей со стороны воды на нижнюю, верхнюю и боковую грани куба. Найдите векторную сумму сил, действующих со стороны воды на куб.
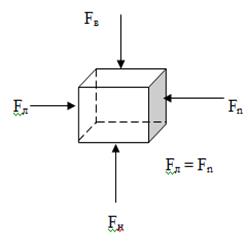
Рис.4.17
Решение. Площадь каждой грани равна ω = 0,04 м2, значение абсолютного давления:
р = р0 + r g h, где р0 = 105 Па – внешнее давление, h – расстояние от пьезометрической поверхности до центра тяжести рассматриваемой поверхности площади ω. Сила давления :
F = рω = (р0 + r g h) ω = р0 ω + r g h ω;
а) для нижней грани h = 1м и Fн = 4392 Н;
б) верхняя грань h = 0,8м и Fв = 4314 Н;
в) боковая грань h = 0,9м и Fб = 4353 Н.
Все силы, действующие на боковые грани, уравновешивают друг друга FS = Fн - Fв = 78 H
Ответ: Fн = 4392 Н, Fв = 4314 Н, Fб = 4353 Н, F = 78 Н.
Пример 8.Пирамидапредставляет собойправильный тетраэдр, нижняя грань которого а, полностью погружена в жидкость плотностью r, находится на глубине h (рис.4.18). Определить силу, действующую со стороны жидкости на боковую грань тетраэдра, если атмосферное давление равно р0.
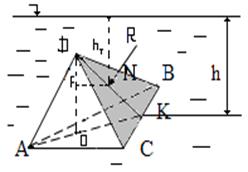
Рис.4.18
Решение. Сила давления жидкости на боковую грань пирамиды: F = (P0 + r g hб) ω = (P0 + r g hб) 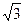 /4 . a2 =
/4 . a2 = 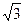 /4 P0 a2 +
/4 P0 a2 + 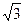 /4 . a2r g hт , где hт – расстояние от центра тяжести наклонной поверхности (треугольника) до пьезометрической поверхности.
/4 . a2r g hт , где hт – расстояние от центра тяжести наклонной поверхности (треугольника) до пьезометрической поверхности.
hт = h – OF = h – 1/3 OD (т.к. NK = 1/3 DК)
АО = 2/3 АК = 2/3 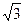 /2 a = а/
/2 a = а/ 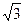 , высоту пирамиды находим как:
, высоту пирамиды находим как:

 ОD = ÖАD2 – АО2 = Öа2 – а2/3 =
ОD = ÖАD2 – АО2 = Öа2 – а2/3 = 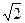 /
/ 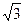 а.
а.
Отсюда глубина погружения центра тяжести треугольной поверхности СDB будет:
hт = h – 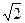 /3
/3 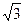 а = (3
а = (3 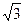 h -
h - 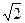 a) / 3
a) / 3 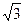 , и искомая величина силы F:
, и искомая величина силы F:
F = 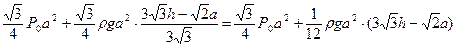 .
.
Ответ: F = 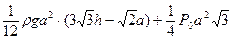 .
.
Пример 9. Вертикальная стенка шириной L= 3 м (в направлении, перпендикулярном плоскости чертежа), шириной b = 0,7 м и высотой Н = 2,5 м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды Н1 = 2 м, в правой – Н2 = 0,8 м. Найти величину опрокидывающего момента, действующего на стенку, определить kуст, сделать вывод: будет ли стенка устойчива против опрокидывания. Плотность материала стенки rст = 2500 кг/м3.
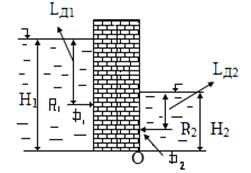
Рис.4.19
Решение. Найдем силу давления воды на стенку слева. Так как на поверхности давление атмосферное, то пьезометрическая плоскость совпадает со свободной поверхностью жидкости. Давление в центре тяжести смоченной поверхности (рис.4.19) слева: Рт = r g H1/2; сила давления R1 = r g H1/2.L.H1 = 58,8 кН.
Координата центра давления смоченной поверхности стенки слева: LД1 = Lт + J0/ Lт ω.
Для прямоугольной стенки J0 = LH13/12,тогда
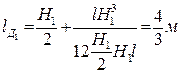 .
.
Точно так же справа: R2 = r g H2/2.L.H2 = 9,41 кН;
LД2 = 2/3 Н2 = 0, 533 м.
Опрокидывающий момент, т.е. момент сил давления жидкости относительно точки О:
Мопр = R1(Н1 – 2/3Н1) –R2(Н2 – 2/3Н2) = 3,67∙104 Н·м.
Удерживающий момент силы тяжести относительно точки О:
Муд = Н·L·b·rстg b/2 = 4,5∙104 Н·м.
Коэффициент устойчивости kуст = Муд/Мопр = 1,23.
Ответ. Запас устойчивости составляет 1,23, поэтому стенка будет устойчива при данных условиях.
Пример 10. Для слива жидкости из бензохранилища имеется квадратный патрубок со стороной h = 0,3 м, закрытый крышкой и шарнирно закрепленной в точке О (рис.4.20). Крышка расположена под углом a = 45° к горизонту. Определить силу натяжения троса Т, необходимую для открытия крышки АО, если уровень бензина Н = 3 м, а давление над ним, измеренное манометром, составляет Рм = 5 кПа, плотность бензина принять 700 кг/м3, вес крышки и трение в шарнире не учитывать.
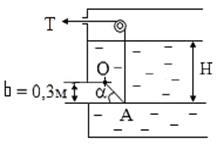
Рис.4.20
Решение. Давление над свободной поверхностью отличается от нормального атмосферного давления, поэтому определим высоту пьезометрической поверхности hр:
hр = (р0 – рa)/r g = Dр/r g = рм /r g = 0,729 м.
Найдем силу давления на стенку АО. Рассматриваемая поверхность является наклонной квадратной стенкой с высотой, равной h/sina, и шириной h. Найдем площадь поверхности: ω = h2/sina.
Центр тяжести этой стенки находим на глубине:
Нт = Н – h/2, Dp = pм, т.е.
R = [Pм + r g (H – h/2)]ω = 3,13 кН.
Расстояние от центра тяжести стенки до пьезометрической поверхности (находится по координате L –идущей вдоль поверхности стенки до пересечения с пьезометрической плоскостью) Lт (рис.4.21).
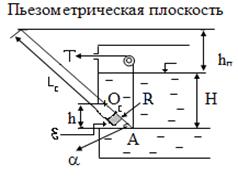
Рис.4.21
Тогда 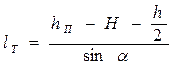 = 5,06 м.
= 5,06 м.
Центральный момент инерции квадратной стенки относительно горизонтальной оси, проходящей через центр тяжести стенки: J0 = (h/sina)3 h/12 = h4/12sin3a.
Расстояние между центром давления и центром тяжести крышки - эксцентриситет ε - определяем по формуле (4.4):
ε = J0/Lт ω =( h4/12sina)/12 Lт sin3a h2 = h2/12 Lт sin2a = 0,003 м.
Найдем силу натяжения троса из уравнения моментов сил, взятых относительно оси шарнира О: Т. OA·cosa - R (OС +ε) = Т·h – R (OC + ε) = 0 , выражая из равенства значение для Т и подставляя численные значения параметров, найдём:
Т = [R (OС +ε)]/h = [R (h/2sina + ε)]/h = 2,24 кН.
Ответ: Сила натяжения троса Т = 2,24 кН.
Ответы, указания к решению задач
1. Определить величину сил давления и точки из их приложения с каждой стороны щита. Найти равнодействующую этих сил. Величины сил реакций находить из уравнения моментов сил. Rк = 40,47 кН, Rш = 76,85 кН.
2. R = 15,2 кН, Lд = 3,8 м. 
3. R = (1/2)[ ρgb(h22 – h12); Lд = 2h2/3 – h12 /3 (h1 + h2).
4. Составить уравнение моментов сил относительно точки О , откуда Т = 47,4 кН.
5. Определить силу давления воды на стенку и координаты центров давления слева и справа. Сравнить опрокидывающий момент силы R с удерживающим моментом от силы тяжести G относительно точки О. Определить kуст , сделать вывод.
6. Определить силу давления и центр давления смоченной прямоугольной поверхности со стороной АО с учетом величины давления над свободной поверхностью. Составить уравнение моментов относительно оси шарнира О, откуда найти величину силы натяжения троса Т.
7. Определить положение пьезометрической поверхности. Площадь клапана представляет собой эллипс. Положение центра давления от пьезометрической поверхности определять по координате, совпадающей по направлению с плоскостью поверхности клапана АВ. М = 620 Н·м.
8. R = 92,3 кН; Lд = 6,01 м.
12. Построить в выбранном масштабе эпюры гидростатического давления на щит слева и справа. Разность площадей этих эпюр (площадь трапеции), умноженная на ширину щита, будет численно равна искомой силе R.
13. Силу давления рассчитывать на 1 м ширины щита.
14. Результирующая сила R равна алгебраической сумме сил R1 и R2 давлений воды слева и справа. R = 180,30 кН.
15. Lд = 0,77 м.
16. Составить уравнение моментов сил R1 и R2 и Т относительно оси вращения затвора. Т = 126,13 кН.
17. Построить в выбранном масштабе эпюры гидростатического давления на щит слева и справа. Разность площадей этих эпюр (площадь трапеции) умноженная на ширину щита будет численно равна искомой силе R. Для нахождения центра давления D необходимо определить центр тяжести полученной после построения фигуры, и провести через него перпендикуляр к плоскости затвора. Примеры нахождения центра тяжести некоторых плоских фигур приведены в Приложении Г (см. Таблицу Г.2).
18. Для нахождения положения центра давления необходимо определить центр тяжести полученной трапеции (из разности эпюр треугольников), через который провести перпендикуляр к плоскости щита. Точка пересечения перпендикуляра с плоскостью щита является искомым центром давления. Измерив отрезок от пьезометрической поверхности до центра давления и умножив эту величину на выбранный масштаб, получим координату Lд.
19. Lд = 3,33 м; kуст = 4,37
20 -26. Использовать табличные значения для определения координат центров тяжести, центрального момента инерции. ( См. Приложение Г Таблица Г.1) или учебник [1].
27. Щит опрокинется при условии, что центр давления будут совпадать или быть выше центра закрепления оси О. Н ≥ 3,38 м.
36. R = 1007,16 Н.
37. Сила давления жидкости на боковую наклонную стенку: F = (ρgh2b)/2sinα. Сила f, с которой боковые стенки действуют на дно сосуда, направлена вверх и равна: f = 25806 Н.
38. R = 1,42 кН; Lд = 0,051 м.
39. R= 2247 Н, Lд = 0,347 м.
40. рвак = 19,82 Па.
41. R = 168 кН; Lт = 2,8 м, Lд = 2,91 м.
42. Полная сила давления численно равна объёму эпюры давления (треугольная призма шириной 1 м).
43. Полную силу давления находить по правилу сложения векторов.
44.R = 26,582 кН; Lд = 7,005 м.
45 - 46. Учесть вес призмы и величину вертикальной составляющей Ry . Плотность бетона принять за 2000 кг/м3.
47. R = 148,3 кН; Lд = 1,89 м. Для нахождения центра давления графоаналитическим способом необходимо найти центр тяжести трапеции KFBC (см. Приложение Г), через центр тяжести провести силу R перпендикулярно поверхности затвора. Измерить расстояние от пьезометрической поверхности (в данном случае свободной) до точки пересечения силы R с поверхностью (точка D) получим величину Lд. Графические построения выполнять в масштабе (рис.4.66).
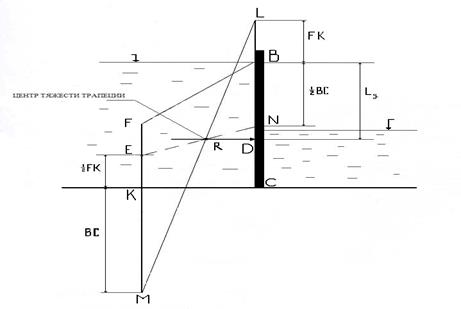
Рис.4.67
48. R = 329,7 кН, Lд = 5,45 м.
49. Составить уравнение моментов всех действующих сил относительно шарнира О. Сила тяжести затвора приложена к его центру тяжести.
Вычислить искомую начальную величину подъёмного усилия Т.
Таблица 4.2. Ответы к вариантам заданий для самостоятельной работы
| Вариант | Величина силы R, кН | Вариант | Величина силы R, кН |
Примеры решения задач
Пример 1. Определить величину гидростатического давления жидкости на внутреннюю поверхность стенки трубы (рис.5.2). Определить Rmax - величину предельного напряжения в стенках трубы для её разрыва, если Н – напор, под которым в трубе находится жидкость; d – диаметр; L – длина трубы; δ – толщина стенки; Rх – сила давления жидкости внутри трубы, способная разорвать ее.
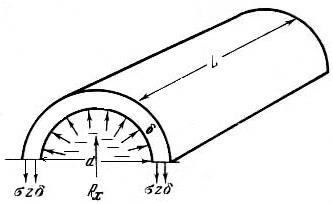
Рис.5.2
Решение. Величина Rх рассчитывается по формуле:
Rх=rgHLd , (1)
где rgH = Pmax – предельная величина гидростатического давления в стенках трубы для её разрыва.
Разрывающей силе давления жидкости противодействует сила сопротивления материала стенки F:
F=2σδL , (2)
где σ – напряжение на разрыв; δ – толщина стенки; L – длина трубы; 2 – коэффициент, поскольку сила сопротивления действует с двух сторон.
При условии, что система находится в равновесии, приравняем силы давления жидкости и сопротивления материала стенки Rх=F. Подставляя из формул (1) и(2) величины, получим:
PmLd=2δσLd или Pmd=2δσ
Откуда
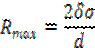
Пример 2. Вертикальный цилиндрический резервуар, диаметром d закрыт сверху полусферической крышкой того же диаметра, весом G и целиком заполнен водой (рис.5.3). Затем в отверстие в верхней части крышки ввернули вертикальную трубку пренебрежительно малого диаметра и залили в неё воду. Определить при какой высоте h вертикальная составляющая силы давления воды на крышку уравновесит ее вес.
Дано: d = 2м; G = 19,6 кН; r = 1000 кг/м3.
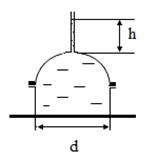
Рис.5.3
Решение. Запишем уравнение, из которого можно определить высоту h:
Rz = G.
Здесь Rz – вертикальная составляющая силы давления воды на полусферическую крышку, а G – вес крышки.
Определяем силу Rz .
Вертикальная составляющая силы давления жидкости на криволинейную поверхность равна весу жидкости в объёме давления:
Rz = r g Wд.
В свою очередь, чтобы построить объём давления Wд, необходимо спроецировать полусферическую поверхность крышки на пьезометрическую поверхность жидкости (то есть на ту горизонтальную плоскость, где весовое давление жидкости равно нулю). В задаче это плоскость MN. Объём, заключённый между полусферой АВ, её проекцией на плоскость MN и вертикальными проектирующими поверхностями, и есть объём тела давления (заштрихован на рисунке 5.4).
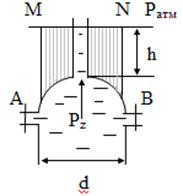
Рис.5.4
Из геометрических построений видно, что этот объём равен разности объёмов цилиндра и полусферы:
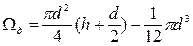
Определяем высоту h из уравнения: G = r g Wд, далее подставляем в результат численные значения параметров, заданных по условию и производим вычисления.
G = r g [ 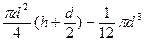 ] Þ
] Þ
h = 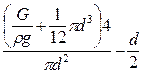
Пример 3. Определить величину,
