Осевые моменты инерции простейших однородных тел

Прямолинейный стержень

Вычислим момент инерции прямолинейного стержня длиной АВ=l относительно оси 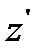, проведенной перпендикулярно стержню через его центр масс С (см. рис. 12).

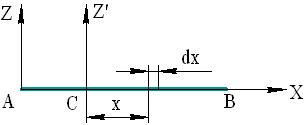
Рис. 12.

Обозначим массу стержня М. Направим вдоль стержня ось x с началом в точке С. Выберем на стержне элементарный участок длиной dx на расстоянии x от начала координат. Обозначим массу этого элементарного участка dm. Очевидно, что 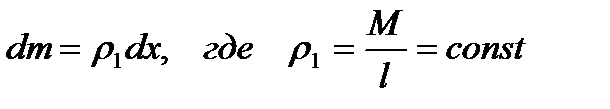- линейная плотность стержня (масса единицы его длины). Тогда момент инерции выделенного элемента равен

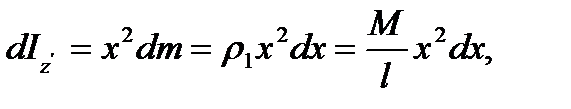
а для момента инерции стержня АВ относительно оси 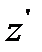получим

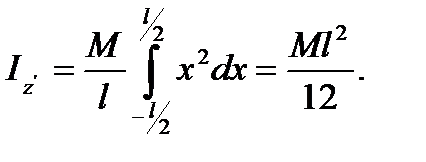(26)

Вычислим с помощью теоремы Штейнера момент инерции стержня относительно оси z , проходящей через конец стержня:

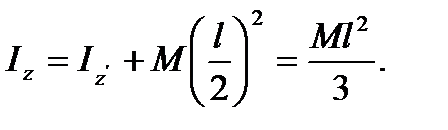(27)

Круговое кольцо

Вычислим момент инерции кругового кольца массой М и радиуса R относительно оси 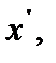проведенной перпендикулярно плоскости кольца через его центр масс С (см. рис. 13). Учитывая, что расстояние от каждой точки кольца до рассматриваемой оси равно R, получим:

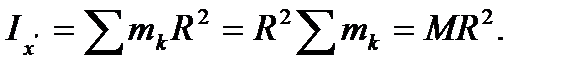(28)

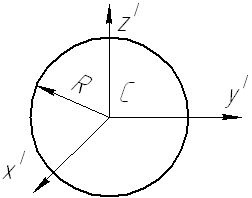
Рис. 13.

Круговой диск

Рассмотрим круговой диск массой М с радиусом R . Вычислим его момент инерции относительно оси 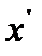(см. рис. 14).

В качестве элемента поверхности диска выберем тонкое кольцо радиуса r и толщиной dr . Массу этого элемента dm можно выразить через его площадь 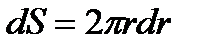и поверхностную плотность :

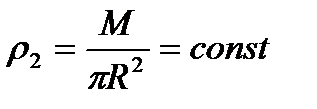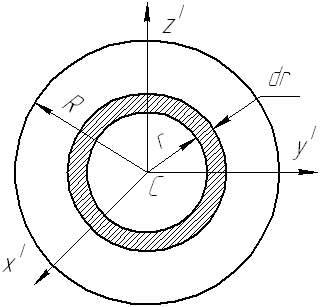
Рис. 14.

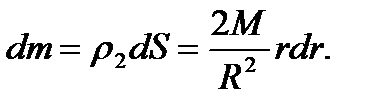
Момент инерции выбранного элемента относительно рассматриваемой оси в соответствии с (28) будет

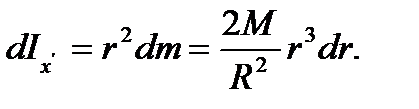
Тогда для искомого момента инерции диска получим

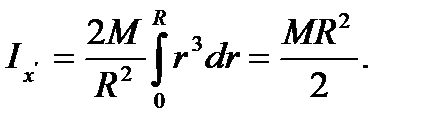(29)

Момент инерции тела относительно произвольной оси.

Эллипсоид инерции

Выведем общую формулу для момента инерции тела относительно произвольной оси l. Выберем на этой оси некоторую точку О, которую примем за начало декартовой системы координат. Обозначим α, β, γ углы, образованные осью l с осями Ox, Oy, Oz (см. рис. 15).

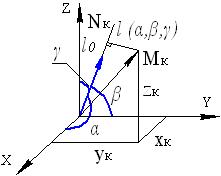
Рис.15

Возьмем точку тела 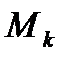с координатами 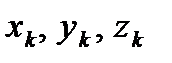и массой 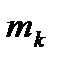. Обозначим расстояние от этой точки до оси l через 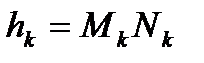(см. рис. 15). Выразим единичный вектор оси l 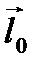через орты координатных осей

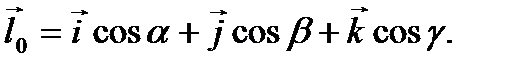
Далее вычислим расстояние 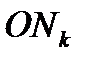как скалярное произведение радиуса-вектора точки 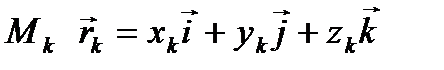и вектора :

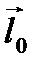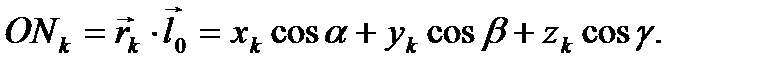
Теперь по теореме Пифагора можно найти (при вычислениях учтем, что )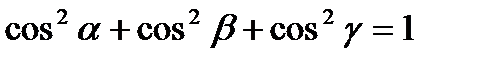

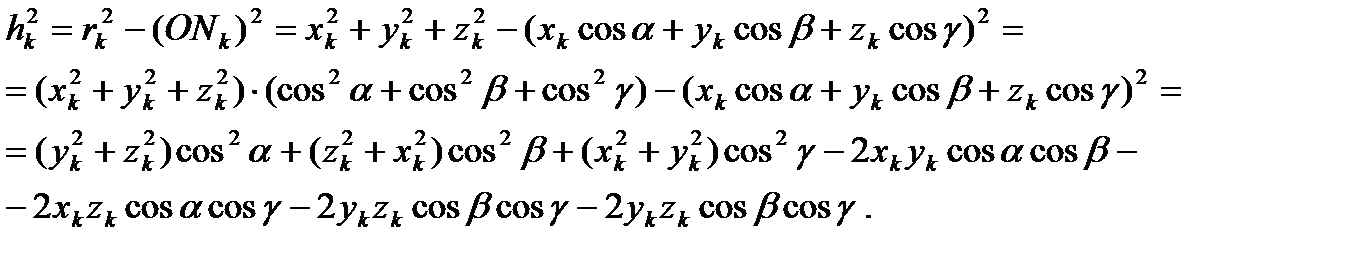
Момент инерции тела относительно оси l согласно определению равен

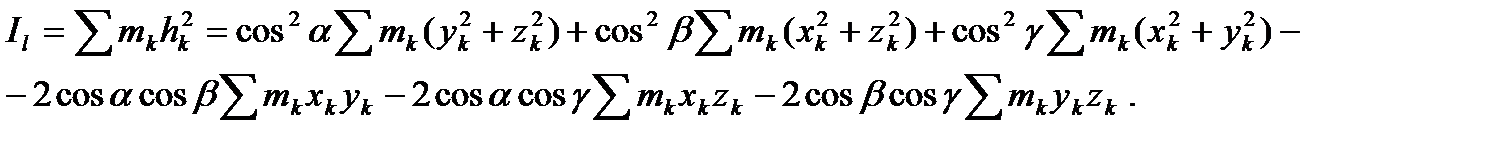
С учетом формул (22) - (23) окончательно выражение для 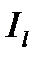запишется в виде

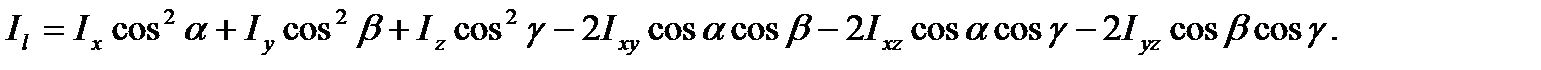(30)

Таким образом, для определения по формуле (30) момента инерции тела относительно любой оси, проходящей через точку О, нужно знать осевые и центробежные моменты инерции относительно координатных осей, связанных с точкой О.

Зависимость осевого момента инерции тела от направления оси может быть представлена следующим геометрическим построением. Проведем через начало координат пучок осей и на каждой оси l , направление которой определяется углами 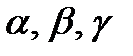, отложим отрезок 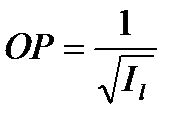(см. рис. 16). Для координат точки Р будем иметь

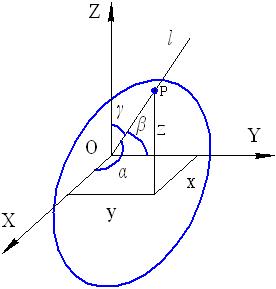
Рис. 16

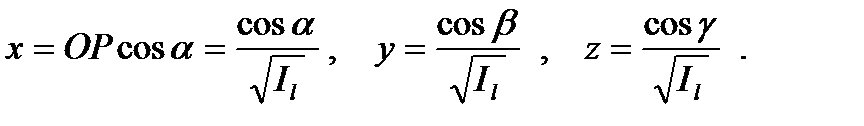
Подставляя в (30) выражения

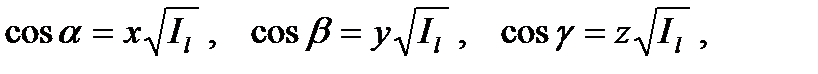
получим после сокращения на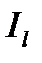

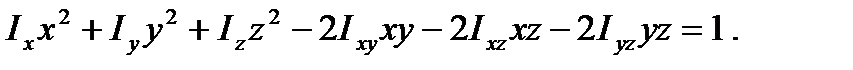(31)

Это уравнение геометрического места точек Р, удаленных от начала координат на расстояние, обратное корню квадратному из момента инерции относительно оси l . Поскольку 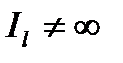, ибо тело имеет конечные размеры, и 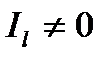, так как точки тела не лежат на одной прямой, то 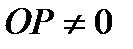и 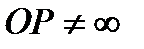. Единственной поверхностью второго порядка, не имеющей бесконечно удаленных точек, является эллипсоид. Поэтому уравнение (31) есть уравнение эллипсоида, называемого эллипсоидом инерции. Эллипсоид инерции меняется в зависимости от выбора точки О.

Эллипсоид инерции, построенный для центра масс тела С, называется центральным.

Главные оси эллипсоида инерции тела 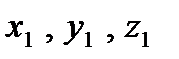в какой-либо точке О называют главными осями инерции тела в этой точке (см. рис. 17).

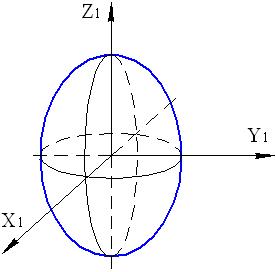
Рис. 17.

Моменты инерции относительно главных осей инерции 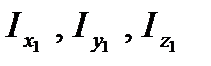называют главными моментами инерции тела в точке О.

Если за оси координат принять главные оси эллипсоида инерции, то уравнение эллипсоида будет иметь вид

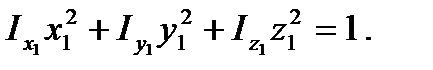(32)

Полуоси этого эллипсоида равны 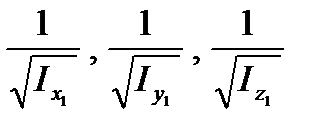, а коэффициенты при произведениях координат в уравнении эллипсоида (центробежные моменты инерции тела относительно главных осей инерции) равны нулю:

.
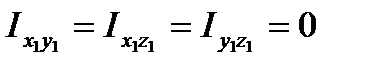