Минимальное остовное дерево. Алгоритмы Прима, Краскала, Борувки
Определение 2.3. Остовное дерево, у которого сумма весов ребер минимальна, назовем минимальным остовным деревом (МОД).
Многие практические задачи сводятся к построению МОД. Например, пусть требуется связать заданное множество населенных пунктов сетью дорог таким образом, чтобы минимизировать связанные с этим затраты. Если известна стоимость создания дороги между каждой парой пунктов – вес соответствующего ребра, то, найдя МОД в полном графе, вершинам которого соответствуют населенные пункты, мы решим задачу. Известно несколько эффективных (полиномиальных) алгоритмов нахождения МОД. Приведем наиболее популярные.
Алгоритм Прима
Идея алгоритма принадлежит Приму. Эффективную технику реализации предложил Дейкстра [4]. Алгоритм состоит из 
итераций. На каждой итерации к частично построенному дереву добавляется одна вершина и одно ребро. Сначала строящееся дерево 
содержит одну произвольную вершину и не содержит ребер. На каждой итерации ищется ребро минимального веса, связывающее вершину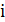 
, принадлежащую 
, с вершиной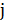 
, не принадлежащей 
и добавляется в дерево: 
, 
,.
Когда 
, алгоритм останавливается, МОД построено.
Эффективная реализация алгоритма [4] заключается в том, что каждой не принадлежащей вершине 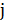приписывается метка 
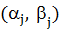, где 
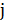– номер ближайшей к вершины из , а 
– вес ребра 
. Тогда после присоединения очередного ребра, метка каждой вершины обновляется с трудоемкостью 
. Число итераций равно , трудоемкость каждой итерации –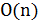 
. Следовательно, общая трудоемкость эффективной реализации алгоритма Прима равна 
.
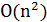Алгоритм Краскала [4]
Алгоритм начинает работу с тривиального графа 
. Упорядочим ребра в порядке неубывания их весов и будем добавлять ребра в 
по порядку. Очередное ребро добавляется в и исключается из списка, если это не приводит к образованию цикла.
В противном случае оно просто удаляется из списка и рассматривается следующее ребро списка. Это повторяется до тех пор, пока число ребер в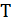 
не станет 
. Построенное дерево – МОД.
Трудоемкость упорядочивания ребер – 
Очевидно, что при построении дерева в худшем случае будут рассмотрены все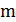 
ребер графа. Пока не построено МОД, частично построенный граф является несвязным, и добавляемое ребро связывает вершины из разных компонент связности. В процессе рассмотрения ребер упорядоченного списка нужно следить, чтобы не возникало циклов, т. е. чтобы не связывались вершины одной компоненты связности. Процедура, описанная в [4] (разделы 2.2.1 и 2.2.2), позволяет это сделать с константной трудоемкостью. Компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае выполняются с трудоемкостью 
где 
– функция, обратная к функции Аккермана [5]. Поскольку для любых практических задач 
, то можно принять ее за константу, таким образом, общая трудоемкость алгоритма Краскала равна 
. Следовательно, этот алгоритм более подходит для построения МОД в графе с небольшим количеством ребер.
Алгоритм Борувки
Алгоритм впервые был опубликован в 1926 г. О. Борувкой в качестве метода нахождения оптимальной электрической сети. Работа алгоритма состоит из итераций, каждая из которых заключается в последовательном добавлении ребер к остовному лесу графа, до тех пор, пока не будет построено одно дерево. В алгоритме предполагается, что веса ребер различны, или ребра как-то упорядочены, чтобы выбиралось единственное ребро с минимальным весом (в случае нескольких ребер, имеющих минимальный вес, выбирается, например, ребро с минимальным номером).
Пусть сначала 
– остовный лес, в котором каждая вершина является деревом. Пока 
, выполнить:
– для каждой компоненты связности (дерева остовного леса) найти ребро минимального веса, связывающее эту компоненту с некоторой другой компонентой связности;
– добавить все найденные ребра в множество ET.
Полученное дерево T является МОД.
На каждой итерации число деревьев в остовном лесу уменьшается не менее чем в два раза, поэтому алгоритм выполняет 
итераций. Трудоемкость одной итерации равна 
, поэтому общая трудоемкость алгоритма – 