Оптимальное дискретное управление при неполной информации. достаточные координаты

Рассмотрим задачу синтеза оптимального управления системой

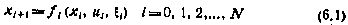
полагая, что измерению доступен некоторый вектор 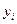связанный с соотношением

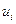Здесь по-прежнему — вектор состояния; — вектор управле­ния; в i-й момент 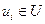; 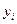— вектор измерения (наблюдения) в тот же момент; 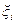, 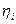— случайные векторы, характеризующие воз­мущения, действующие на систему, и ошибки измерения соответст­венно. Предполагается, что статистические свойства векторов 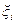, 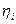полностью известны.

В качестве критерия оптимальности примем

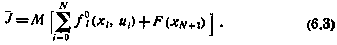
Основная особенность задачи синтеза оптимального управления при неполной статистической информации заключается в следую­щем. Так как вектор фазовых координат не измеряется, то синтези­руемое оптимальное управление в i-й момент времени 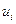должно в общем случае зависеть от всех прошлых и настоящих измерений 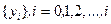, обозначаемых сокращенно через 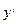. Иными словами, оптимальная стратегия управления является некоторой последовательностью функции 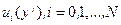, ставящих в со­ответствие всем прошлым и текущим наблюдениям векторы управ­ления из условия минимума критерия (6.3). Эта оптимальная стратегия может быть найдена с помощью достаточных условий опти­мальности в форме метода динамического программирования. Ос­новное рекуррентное соотношение при этом принимает вид

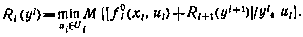
Здесь через 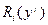обозначена функция будущих потерь, представ­ляющая собой минимальное значение критерия (6.3), которое может быть достигнуто при оптимальном управлении системой (6.1) начиная с момента времени i по наблюдениям (6.2), получен­ным в моменты .

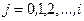Граничным условием для функции 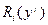, как и при управле­нии при полной информации, может служить равенство

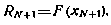
Согласно рекуррентной процедуре синтез оптимальных управ­лений должен производиться в следующем порядке

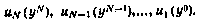
Синтез сводится к вычислению на каждом шаге функции буду­щих потерь 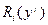, раскрытию операции математического ожида­ния и оптимизации по правой части основного рекуррентного соотношения. Для раскрытия операции математического ожидания необходимо в свою очередь вычисление условных плотностей 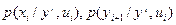. В общем случае эти плотности вычислить очень трудно. Принципиальная трудность заключается в необходи­мости запоминания всех прошлых и настоящих измерений .

Задача значительно облегчается, если предположить существо­вание некоторого вектора 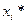, который обычно называется векто­ром достаточных координат (статистик), являющегося функцией от и удовлетворяющего следующим условиям:

1) знание вектора 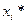достаточно для определения оптимально­го управления 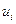и функции будущих потерь 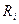. Это означает, что плотности типа 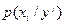могут быть представлены в виде ;

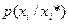2) знание вектора 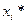в любой момент достаточно для опреде­ления собственной будущей эволюции, т. е. для моментов j>i. В этом случае основное рекуррентное соотношение может быть представлено в виде

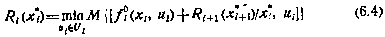
с прежним граничным условием

Применение соотношения (6.4) упрощает решение задачи синтеза за счет того, что функция будущих потерь теперь зависит от векто­ра 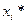вполне определенной размерности для всех моментов, в то время как размерность совокупности увеличивается с возраста­нием номера i. С введением понятия достаточных координат исходная задача синтеза оптимального управления при неполной инфор­мации может быть условно разделена на две: определение доста­точных координат и определение оптимального управления как функции достаточных координат. Соответственно оптимальный, регулятор, получаемый в результате решения задачи, состоит и» двух блоков — блока обработки измерительной информации и бло­ка оптимального управления. Строго говоря, синтез обоих блоков необходимо осуществлять совместно. Однако в некоторых случаях, например, для линейной системы с аддитивным возмущением к квадратичным критерием оптимальности оказывается справедли­вой так называемая теорема разделения, согласно которой задача, определения достаточных координат отделяется от задачи синтеза собственно оптимального управления. Эта теорема с успехом мо­жет быть использована для приближенного решения задачи в об­щем случае.