Построение эпюр изгибающих моментов
Как тонко подметил Архимед, любая сила, приложенная с некоторым плечом относительно рассматриваемой точки, создает вращающий момент. И чем больше плечо, тем больше значение вращающего момента при одном и том же значении приложенной силы.
Это правило рычага действительно и при построении эпюр изгибающих моментов. Вот только моменты называются не вращающими, а изгибающими, но суть от этого не меняется. Так предполагается, что в любом поперечном сечении балки, находящемся на расстоянии х от начала балки (начала координат) могут действовать изгибающие моменты.
Например в нашем случае в начале балки приложена сосредоточенная сила - опорная реакция А = 6 кг, соответственно эта сила будет создавать изгибающий момент Ах, где х - плечо действия силы. При этом равномерно распределенная нагрузка также будет создавать изгибающий момент. А чтобы определить значение этого момента, сначала определяется общее значение нагрузки -qx, что мы и делали при построении эпюры поперечных сил. Общее значение распределенной нагрузки в рассматриваемом сечении можно рассматривать как равнодействующую сосредоточенную силу, а прикладывается эта сила в центре тяжести эпюры нагрузки. Т.е. в этом случае мы рассматриваем эпюру нагрузки, как некое физическое тело, имеющее плотность и соответственно центр тяжести. Впрочем с точки зрения теории сопротивления материалов в этом нет ничего удивительного.
Определить положение центра прямоугольной эпюры нагрузки несложно. Подобными упражнениями мы занимались в школе, когда определяли центр тяжести линейки. И находится этот центр тяжести посредине длины линейки, а в данном случае посредине рассматриваемой части эпюры нагрузки и составляет х/2.Таким образом плечо действия равнодействующей сосредоточенной силы при равномерно распределенной нагрузке составляет х/2. При этом функциональное уравнение изгибающих моментов, необходимое для построения эпюры моментов, будет иметь следующий вид:
M = Ax - qx·x/2 = Ax - qx2/2 (545.5.1)
Примерно такой же результат мы получим, если проинтегрируем уравнение поперечных сил:
M = ∫(A - qx)dx = M0 + Ax - qx2/2 (545.5.2)
Где М0 = 0 - это опять же постоянная интегрирования. В данном случае - значение момента на опоре А. Так как мы рассматриваем однопролетную безконсольную балку на шарнирных опорах, то в этом частном случае значение момента на опоре А равно нулю. Кроме того значение момента на опоре В для шарнирной безконсольной балки также равно нулю, так как шарнирные опоры повороту сечений ни как не препятствуют. Эта особенность в частности используется при определении опорных реакций однопролетной безконсольной балки на шарнирных опорах. Другими словами, зная, что момент на опоре В равен нулю, мы можем определить значение опорной реакции А из уравнения (45.5.2):
МВ = 0 = Аl - ql2/2 (545.5.3)
A = (ql2/2)/l = ql/2 (545.5.4)
В общем случае значение момента в начале координат может быть не равно 0.
А теперь рассмотрим еще одну особенность изгибающих моментов: для рассматриваемого сечения не имеет принципиального значения, какой будет знак у момента, положительный или отрицательный, так как при любом знаке в сечении будет как растягиваемая, так и сжимаемая зона сечения. А вот какая именно зона сечения будет растягиваемой, верхняя или нижняя - имеет большое значение, потому что не все материалы имеют равное сопротивление растяжению и сжатию, а кроме того форма сечения далеко не всегда бывает прямоугольной.
В связи с этим при построении эпюр изгибающих моментов принято следующее правило:
Эпюра моментов строится с той стороны, где будет растянутая зона сечения. При этом момент, пытающийся вращать рассматриваемое сечение по часовой стрелке, считается положительным, а против часовой стрелки - отрицательным.
Примечание: это правило не является общепринятым. В некоторых справочниках и учебниках по теории сопротивления материалов положительный момент строится сверху от оси х, что в общем то логично, но при этом получается, что положительный момент там, где сжатая зона сечения. В других он строится с той стороны, где растянутая зона сечения, но при этом может показываться со знаком "-", если строится снизу от оси х. Но как я уже говорил выше, принципиального значения это не имеет, главное понимать общий смысл изгибающих моментов.
Если мы посмотрим на направление действия опорной реакции А и распределенной нагрузки q (рисунок 545.4), то увидим, что относительно любого из рассматриваемых сечений опорная реакция А пытается вращать это сечение по часовой стрелке, а распределенная нагрузка q - против. Это означает, что функциональное уравнение, описывающее изменение изгибающих моментов по длине балки, составлено у нас правильно.
При этом растянутой будет нижняя зона сечения балки по той причине, что балка прогнется вниз при таком действии нагрузки. Следовательно эпюру моментов в данном случае следует строить снизу от оси координат х.
Теперь у нас есть все данные для построения эпюры изгибающих моментов. Судя по уравнению (545.5.2) это будет квадратная парабола, а максимальное значение изгибающего момента будет посредине балки, так как нагрузка у нас симметричная, и составит М = 6·2 -3·22/2 = 6 кгм.
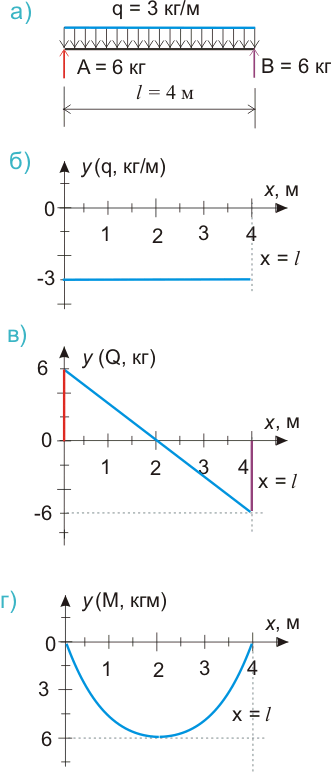
Рисунок 545.5.г) эпюра изгибающих моментов, как график функции у = 6х - 3х2/2
В общем случае, когда нагрузка несимметричная, как показано на рисунках 545.2.а) и б) или на балку действуют несколько распределенных нагрузок, то определить сечение в пролете балки, в котором действует максимальный изгибающий момент. можно, воспользовавшись следующим общим правилом:
