Метод Эйлера решения задачи Коши для ОДУ 1-го порядка.

В общем случае задача Коши решения в аналитическом виде не имеет, поэтому ее решают численными методами, простейшим из которых является метод Эйлера.

Для этого зададимся на оси 0x достаточно малыми шагами 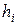. Будем рассматривать решение в точках с координатами 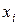(рис. 4.2):

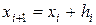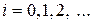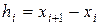, , . (4.3)

Введем обозначения:

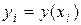; (4.4)

Из начального условия нам известно значение функции 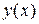в точке 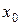: 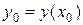. Для определения значения 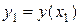в точке 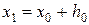запишем следующее равенство:

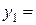
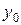
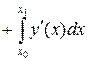(4.5)

Для проверки подставляем значение интеграла .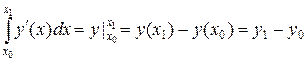

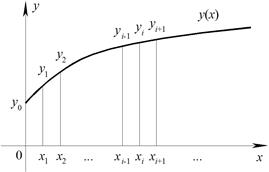
Рис. 4.2. Схема разбиения.

Далее, воспользуемся уравнением (4.1) и заменим под знаком интеграла 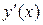на :

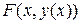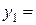
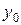
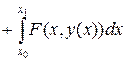(4.6)

Поскольку значение подынтегральной функции на интервале 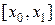нам известно только в точке 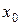, воспользуемся численным интегрированием по формуле левых прямоугольников:

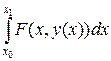
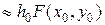(4.7)

Таким образом, приближенное значение 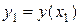можно получить по формуле

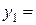
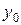
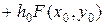
Аналогично можно получить приближенные значения:

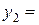
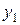
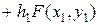
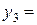
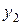
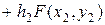
и т.д.

Пользуясь таким алгоритмом, последовательно получим решение для любого количества точек разбиения. Вышеизложенный подход для решения задачи Коши называется методом Эйлера. Общий вид метода Эйлера:

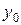– задано

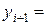
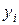
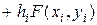(4.8)

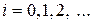
Заметим, что в сложных практических случаях для решения применяются различные модифицированные алгоритмы, связанные с уточнением шага разбиения на каждом шаге пересчета. Среди такого рода модификаций наиболее употребляемыми являются методы типа Рунге-Кутта, излагаемые в соответствующей специализированной литературе. Приведем простейший вариант уточнения метода Эйлера.

Пусть значение 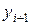, вычисленное по формуле (4.8) будет неокончательным (промежуточным). Обозначим его 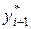, т.е.

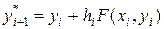(4.9)

Тогда для определения значения интеграла

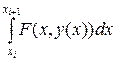
нам на интервале интегрирования 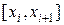известны значения подынтегральной функции в двух точках: 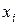и 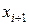. Поэтому можно воспользоваться формулой трапеции, которая на порядок точнее формулы левых прямоугольников:

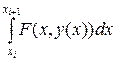
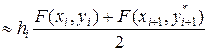(4.10)

Таким образом, общий вид уточненного алгоритма метода Эйлера имеет вид

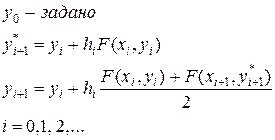(4.11)

Задача Коши для обыкновенного дифференциального уравнения (ОДУ) n-го порядка

Математическая формулировка задачи

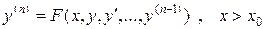(4.12)

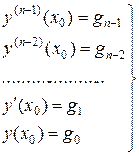– начальные условия (4.13)

Сведение задачи Коши для ОДУ n-го порядка к задаче Коши для системы n ОДУ 1-го порядка

Введем (n-1) дополнительные неизвестные функции по правилу:

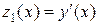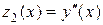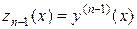, , …, (4.14)

Тогда вместо уравнения (4.12) получим систему ОДУ 1-го порядка:

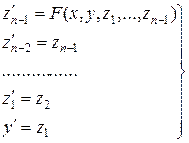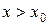, (4.15)

Соответственно, начальные условия приводятся к виду

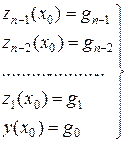– начальные условия (4.16)

Вариант метода Эйлера решения задачи Коши для системы ОДУ 1-го порядка.

Наиболее простым и естественным для численного решения задачи Коши (4.15)-(4.16) представляется следующий алгоритм метода Эйлера:

– для первого уравнения использовать интегрирование по формуле левых прямоугольников (без уточнения),

– для остальных – по формуле трапеции, т.е.:

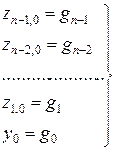– задано (начальные условия)

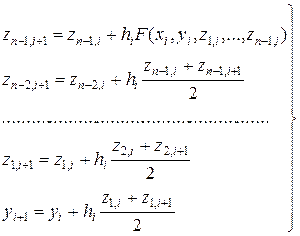
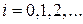(4.17)

Задача об изгибе консоли (задача Коши)

Задание.

Рассмотрим задачу об изгибе консоли, жестко закрепленной с левого края (рис. 4.3).

Определить прогиб консоли (решить задачу Коши)

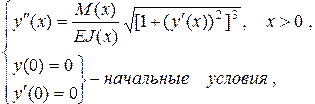(Л4.1)

методом Эйлера.

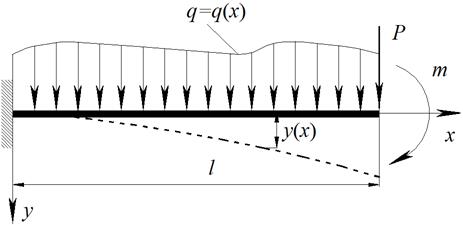
Рис. 4.3. К задаче об изгибе консоли.

Варианты задания.

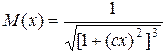– изгибающие моменты в балке (рис. 4.3);

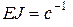– жесткость балки; 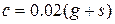– числовой параметр,

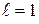– длина балки; 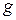– номер группы, 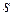– номер студента по журналу.

Принять для расчета на ЭВМ число точек .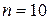

Предварительные построения.

Сводим основное уравнение исходной задачи второго порядка к системе двух дифференциальных уравнений первого порядка:

(Л4.2)

где 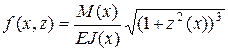.