Алгоритм создания компьютерной модели решения задачи

1. Выбрать на листе Excel ячейки и ввести в них данные с пояснениями

2. Последовательно решать задачу: выполнять действия, расчеты и вносить комментарии к ячейкам, в которых производились расчеты

3. Выделить ячейки с результатами (цветом, шрифтом и др.) и написать вывод

Подсчитать основные статистические характеристики данной выборки с использованием пакета Статистика

Чтобы подключить пакет: Сервис – Надстройки – Analysis ToolPak

Сервис – Data Analysis, появляется диалоговое окно, в котором выбрать Descriptive Statistics.

В появившемся диалоговом окне:

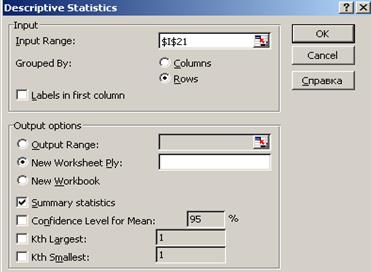
· ввести диапазон анализируемых данных

· Rows

· Summary statistics

· ОК

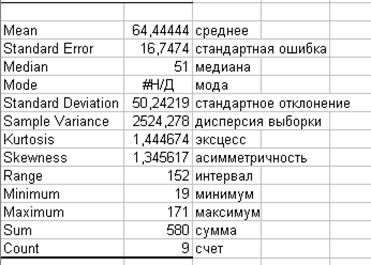
Нажатие ОК возвращает числовые характеристики.

Задание № 4

Провести сравнение статистических характеристик, полученных тремя разными способами в Excel (по арифметическим формулам, по формулам, встроенным в Excel, с помощью пакета). Привести доказательство письменному выводу

Статистические характеристики

1. Средняя арифметическая ряда:

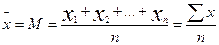
2. Медиана – значение признака, которое находится в середине ранжированного ряда.

Например: 120 125 130 135 140 Þ Me = 130

8 10 12 16 20 28 30 40 Þ Me = (16+20)/2

3. Мода – наиболее часто встречающееся в ряду значение признака.

5.Средняя геометрическая ряда – корень n-ой степени из произведения всех значений варьирующего признака x:

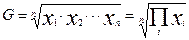, n – число наблюдений.

6. Средняя квадратическая ряда:

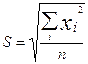
7. Средняя гармоническая ряда:

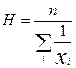
8. Простейшей мерой рассеяния является вариационный размах – разность между наибольшим и наименьшим значениями варьирующего признака.

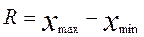
Эта мера рассеяния является лишь приближенной характеристикой варьирующего признака. В практике статистической обработки материала пользуются обычно средним квадратическим отклонением и дисперсией.

9. Среднее квадратическое отклонение:

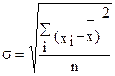, где

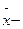среднее арифметическое, 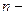число наблюдений..

10. Дисперсия -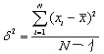

Эксцесс

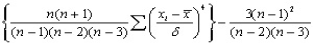
Асимметрия

13. Стандартное отклонение Öd²

14. Среднее абсолютное отклонение:

.

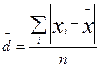15. Коэффициент вариации – отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:

.

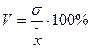Сопоставимость средних величин.

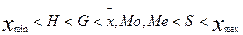
При нормальном распределении .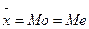

Медиана

Медиана разбивает выборку на две равные части. Пятьдесят процентов наблюдений лежит ниже медианы, пятьдесят процентов — выше медианы. Если значение медианы существенно отличается от среднего, то распределение скошено (более подробно см. главу Элементарные понятия).

Мода

Мода — это максимально часто встречающееся значение в выборке. Частота встречаемости также отображается. Если имеется несколько значений с максимальной частотой, то распределение мулътимодалъно. Если каждое значение встречается лишь одни раз, программа делает запись: моды нет (см. электронную таблицу с результатами).

Геометрическое среднее

Геометрическое среднее — это произведение всех значений переменной, возведенное в степень 1/n (единица, деленная на число наблюдений). Геометрическое среднее полезно, например, если шкала измерений нелинейная.

STATISTICA вычисляет геометрическое среднее с помощью логарифмического преобразования: log(геометрическое среднее) = {a[log(xi)]}/n, где x_i— i-е значение, n — число наблюдений. Если переменная содержит отрицательные значения или нуль (0), геометрическое среднее вычислить нельзя.

Гармоническое среднее

Гармоническое среднее иногда используют для усреднения частот. Гармоническое среднее вычисляется по формуле: ГС = n/S( 1/х_i) где ГС — гармоническое среднее, n — число наблюдений, х_i — значение наблюдения с номером i. Если переменная содержит нуль (0), гармоническое среднее вычислить нельзя.