Тема: «Вычисление односторонних пределов. Исследование функций на непрерывность. Классификация точек разрыва»

Цель работы:научиться вычислять односторонние пределы, исследовать функций на

непрерывность, классифицировать точки разрыва.

Образовательные результаты, заявленные во ФГОС:

Студент должен

уметь:

- применять методы дифференциального и интегрального исчисления.

знать:

- основы дифференциального и интегрального исчисления.

Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.

Методические указания по выполнению работы:

1. Ознакомиться с теоретическим материалом по практической работе.

2. Рассмотрите образцы решения задач по теме.

3.Выполнить предложенное задание согласно варианту по списку группы.

4.Изучить условие заданий для практической работы и выполнить её.

5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.

5. Оформить отчет о работе. Сделайте вывод.

Краткие теоретические и учебно-методические материалы по теме практической работы

Односторонние пределы

Вспомним определение предела функции в точке. Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента х_n¹а, сходящейся к а, последовательность соответствующих значений функции f(x_n), nÎN, сходится к числу В.

В приведенном выше определении предела функции в точке аргумент х принимает значение х_n из окрестности точки а, кроме х=а, как слева, так и справа от а.

Если при нахождении предела рассматривать значения х только слева от а, то такой предел называетсялевым или левосторонними обозначается

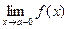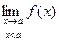; или ,

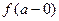если рассматривать значения х только справа от точки а, такой предел называетсяправым или правосторонним и обозначается

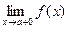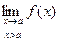; или ,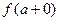

Левый и правый пределы называются односторонними пределами, а предел функции в точке иногда называется двусторонним. В случае, когда изучают односторонние пределы в точке х=0 (т.е. при х®0), запись упрощают и пишут для левостороннего предела 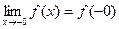, а для правостороннего - .

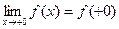Из определений следует, что если у f(x) существует предел в точке а и 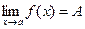, (1)

то односторонние пределы 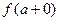и 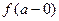также существуют и

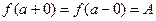, (2)

Верно и обратное утверждение: если имеет место (2), то имеет место и (1).

Таким образом, для установления существования предела функции f(x) в точке а достаточно проверить выполнение следующих трех условий:

а) существование левого предела;

б) существование правого предела;

в) совпадение односторонних пределов.