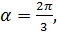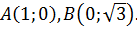Уравнение прямой с угловым коэффициентом.

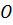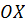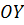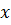Зафиксируем на плоскости декартову прямоугольную систему координат с началом координат в точке и осями координат и . Построим на плоскости некоторую прямую и выясним, как связаны между собой координаты и 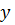ее точек. Составим уравнение этой прямой, то есть уравнение, которому будут удовлетворять координаты всех точек этой прямой и не будут удовлетворять координаты ни одной точки, не принадлежащей ей.

Положение прямой 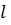на плоскости с выбранной системой координат можно определить различными способами. Соответственно этому выбору уравнение прямой будет иметь в каждом случае свой вид.

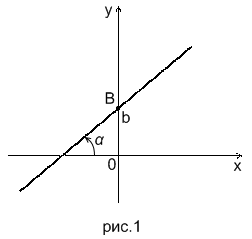
Определение. Углом наклона прямой называется направленный угол 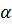, на который нужно повернуть ось 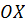, чтобы её положительное направление совпало с одним из направлений этой прямой.

Угол наклона прямой 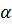может принимать различные значения, отличающиеся друг от друга на величину 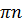, где 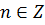. Поэтому в качестве направленного угла наклона берут наименьшее положительное значение угла 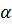. А если прямая параллельна оси 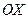, то считают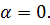

Таким образом, .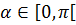

Отметим, что для заданной прямой все значения её угла наклона имеют один и тот же тангенс, т.к. 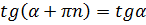, где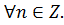

Определение. Тангенс угла наклона прямой называется её угловым коэффициентом.

Обозначим его следующим образом: 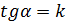. (1)

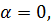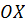В частности, если угол то есть прямая параллельна оси , то 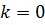; а если угол 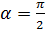, то 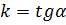не существует, и, так как

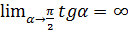, в этом случае прямая параллельна оси ОУ и углового коэффициента не имеет.

Если прямая 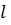не параллельна оси 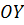, то она пересекает эту ось в некоторой точке 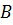, отсекая на оси отрезок 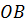, длину которого обозначим через 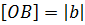. Введем понятие направленного отрезка, а именно, будем считать, что 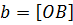, если точка 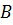лежит выше ос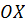и , и 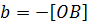в противном случае.

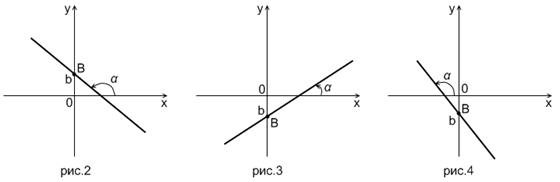
Положение прямой на плоскости определяется однозначно, если заданы величины 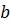и 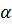. (см. рис. 1,2,3,4)

При любом расположении прямой , не параллельной оси 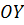, отсекающей на оси 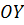направленный отрезок величины 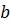и имеющей угловой коэффициент 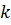, координаты ее точек удовлетворяют уравнению

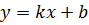(2)

Если же прямая параллельна оси 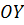, то все ее точки таковы, что для их координат выполняется условие, которое и является уравнением этой прямой:

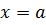, (3)

где 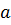- величина отрезка, отсекаемого прямой на оси .

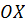Уравнение вида 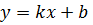(2) называется уравнением прямой с угловым коэффициентом.

Пример 1. В прямоугольной системе координат построим прямую, заданную уравнением .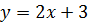

Решение. Сравним данное уравнение с уравнением прямой вида (2). Угловой коэффициент прямой, уравнение которой дано в условии, 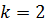. Отрезок, отсекаемый ею от оси ОУ, имеет величину 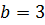, т.е. этой прямой принадлежит точка 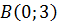. (см. рис.1)

Так как 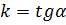(см.(1)), а тангенс острого угла 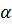в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, можно определить положение прямой, построив прямоугольный треугольник 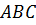с катетами 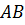, параллельным ос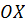и , и 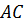, параллельным оси 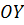, такими, что их длины 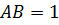и 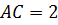. (см.рис. 5)

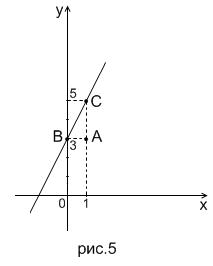
Тогда 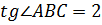, т.е. угол при вершине 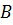является углом наклона 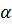заданной прямой. Отрезок 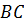принадлежит заданной прямой. Продолжив его, строим саму прямую.

Пример 2. Составим уравнение прямой, пересекающей ось 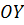в точке 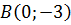и проходящей через точку .

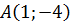Решение. Построим в системе 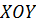прямую, проходящую через заданные в условии точки, и выясним, чему равны ее угловой коэффициент 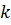и величина 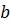. По этим двум параметрам составим искомое уравнение, взяв за исходное уравнение 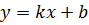(2). (см. рис.6)

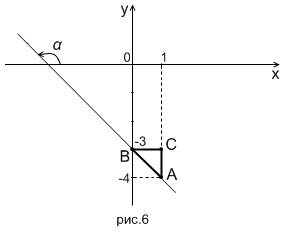
Из рис.6 следует, что величина 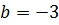и угол наклона прямой 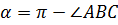. Сравните с рис.4. Очевидно, что координаты точки 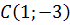. Острый угол 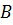в треугольнике 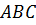имеет тангенс 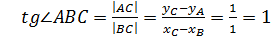. Тогда угловой коэффициент данной прямой 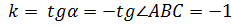. (см.(1)).

Подставляем найденные 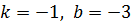в уравнение (2) и получаем .

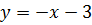Ответ: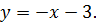

Общее уравнение прямой.

Отметим, что уравнения прямой вида (2) и (3), рассмотренные ранее, являются линейными. Имеет место следующая теорема.

Теорема. Множество точек 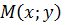плоскости принадлежит прямой тогда и только тогда, когда их координаты удовлетворяют линейному уравнению, а именно, уравнению вида

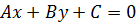, где 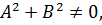(4) то есть 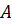и 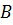одновременно не равны нулю.

Уравнение вида (4) называется общим уравнением прямой на плоскости.

Все рассмотренные уравнения прямой связаны между собой. Так, например, пр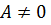и и 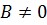уравнение (4) приводится к уравнению с угловым коэффициентом вида (2): 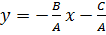, где .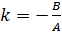

При 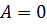, 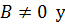равнение (4) после преобразования приводится к уравнению вида 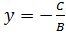с угловым коэффициентом .

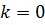При 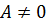, 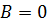получаем из (4) уравнение 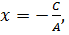что соответствует уравнению вида (3).

Обратно, если уравнение с угловым коэффициентом вида (2) переписать в виде 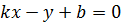, то оно будет соответствовать общему уравнению вида (4).

Пример 3. Выясним, под каким углом прямая 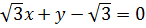пересекает ось 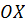, и найдем точки ее пересечения с осями координат.

Решение. Приведем уравнение заданной прямой к виду (2), то есть запишем её уравнение с угловым коэффициентом. Выразив 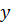из исходного уравнения этой прямой, получим уравнение .

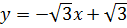Отсюда следует, что 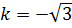и 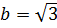. Следовательно, искомый угол 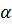таков, что 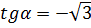(см.(1)), т. е. 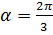- угол, под которым данная прямая пересекает ось .

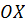Ось 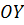пересекается прямой в точке 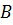с ординатой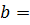 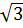, т. е. в точке 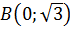. (см. рис.2)

Чтобы найти точку 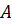, в которой прямая пересекает ось 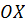, учтем, что в этой точке координата 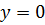, и подставив в уравнение заданной прямой

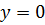, получим 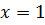. Т.е. координаты точки .

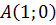Ответ.