Расчёты на жёсткость при изгибе.

Работающие на изгиб элементы строительных и машиностроительных конструкций во многих случаях должны быть рассчитаны не только на прочность,но и на жёсткость.

При этом зачастую оказывается, что требуемые размеры поперечного сечения бруса (балки), определённые из расчёта на жёсткость, получаются большими, чем требуемые по условию прочности.

В большинстве случаев условие жёсткости выражается неравенством

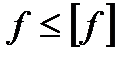, (7.27)

т.е. максимальный прогиб (стрела прогиба 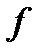) не должна превышать допускаемого 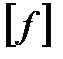.Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставиться дополнительное условие жёсткости – ограничение угла поворота опорных сечений:

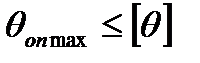. (7.27а)При этом допускаемый угол поворота составляет в среднем 0.001 рад.

Пример 1. Одноопорная балка нагружена сосредоточенными силами и распределенной нагрузк6й (рис. 31.1). Построить эпюры поперечных сил и изгибающих моментов.

Решение

Задачу решаем с помощью составления уравнений поперечных сил и изгибающих моментов в поперечных сечениях балки.

При проверке эпюр используем дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом:

1. Производная от поперечной силы по длине балки равна интенсивности распределенной нагрузки

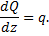
2. Производная изгибающего момента по длине балки равна поперечной силе

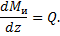
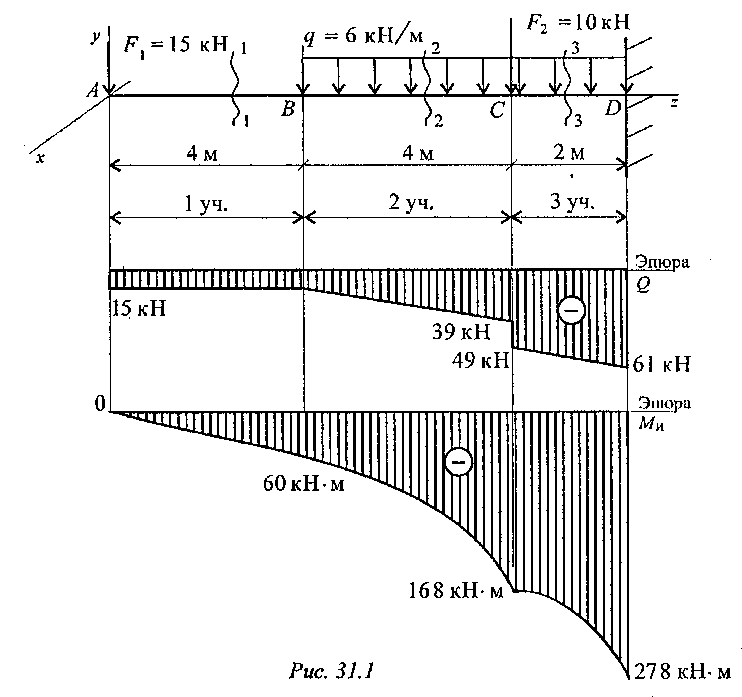
Рассмотрим участок 1, сечение 1.

Поперечная сила Q₁ = - F₁= -15 кН.

По принятому правилу знаков поперечная сила отрицательна и постоянна на этом участке.

Изгибающий момент M_x1 = -F₁z₁.

0 ≤z₁≤ 4 м: М_А = 0; М_В= -15∙4 = -60 кН∙ м.

Рассмотрим участок 2, сечение 2.

Поперечная сила Q₂ = -F₁ - q(z₂ - 4).

4 м ≤ z₂≤ 8 м: Q_B = -F₁ = -15 кН; Q_C^слева = -39кН.

Поперечная сила изменяется по линейному закону.

Изгибающий момент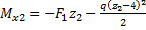

4 м ≤z₂≤ 8 м:

при z₂ = 4 м изгибающий момент M_B= -6О кН∙м. В точке В нет внешнего момента, поэтому изгибающий момент слева и справа от точки В одинаков. В этом случае рассчитывать его дважды не следует;

при z₂ = 8 м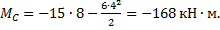

Рассмотрим участок 3, сечение 3.

В точке С приложена внешняя сила F₂. На эпюре должен быть скачок, равный приложенной силе; на эпюре моментов должен быть излом.

Поперечная сила на участке 3: Q₃ = -F₁ - q(z₃ - 4) - F₂;

при z₃ = 8 м Q_C^справа = -15 - 6·4 -10 = -49 кН;

точка С: Q_C^слева = 39 кН; Q_С^справa = 49 кН;

при z₃ =10м Q_D =-15-6·6-10= - 61кH.

Поперечная сила изменяется по линейному закону.

Изгибающий момент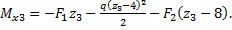

8 м ≤z₃≤ 10 м:

при z₃ = 10 м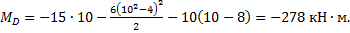

На участках 2 и 3 эпюра изгибающих моментов ограничена квадратичной параболой.

По полученным результатам, учитывая дифференциальные зависимости между поперечной силой и изгибающим моментом, строим эпюры Q и М_х. На втором u третьем участках поперечная сила не имеет нулевых значений, поэтому на эпюре моментов нет экстремумов.

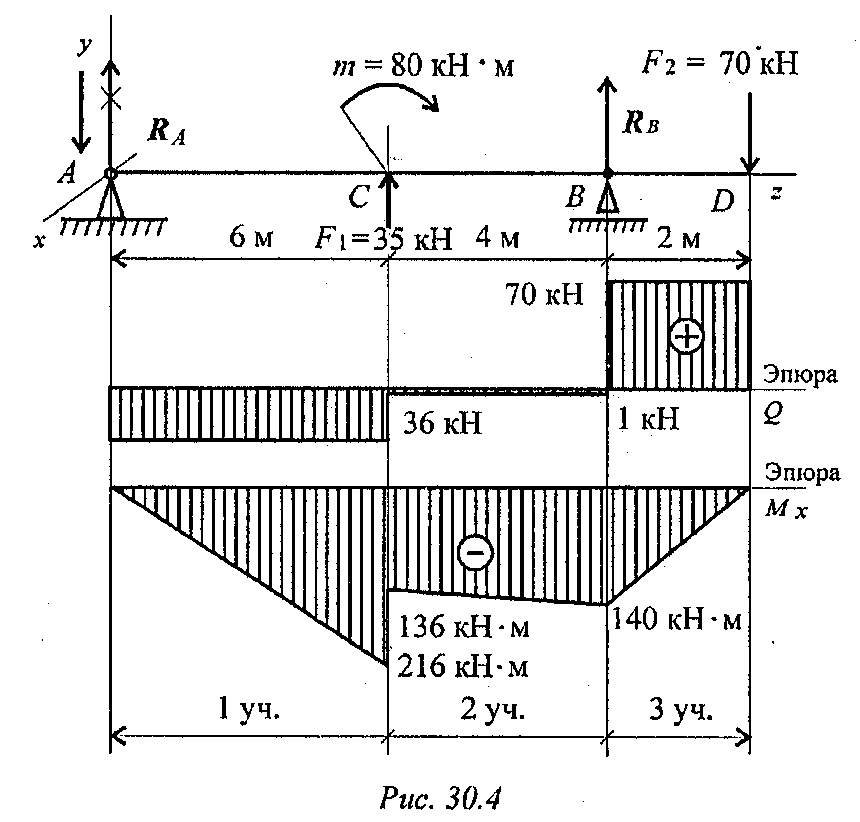
Пример 2. На двухопорную балку действуют сосредоточенные силы и моменты (рис. 30.4). Построить эпюры поперечных сил и изгибающих моментов.

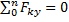Для двухопорной балки построение эпюр начинают с определения опорных реакций балки. Для их определения используем систему уравнений равновесия, составляем два уравнения моментов относительно шарнирных опор. Затем проводим проверку правильности решения по уравнению

Решение

1. Определение реакций в опорах.

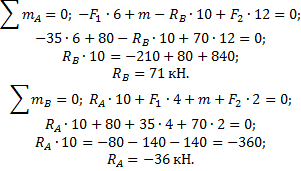
Реакция в опоре направлена в обратную сторону.

Проверка: ∑F_y = 0;

-R_A + F₁ + R_B - F₂ = 0; -36 + 35 + 71-70 = 0.

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным, точкам, без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр..

Участок 1 (от точки А до точки С).

В точке А приложена реакция R_А, направленная вниз. Поперечная сила на участке постоянна: Q₁ = R_A = -36 кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F₁ = 35 кН, направленная вверх, - здесь возникнет скачок вверх на величину 35 кН.

Момент в точке С (слева) может быть рассчитан по известной зависимости М_С^слева = R_A∙ 6; М_С^слева = -36·6 = -216 кН∙м.

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Q_c = -R_А + F₁;

Q_c = -36 + 35 = -1 кН.

В точке С приложена внешняя пара сил с моментом 80 кН∙м, следовательно, здесь проявляется скачок на величину приложенного момента: М_С^справа = M_C^слева + m;

M_C^справа= -216 + 80 = 136 кН∙м.

Поперечная сила на втором участке постоянна: Q_С = Q_С^справа.

Момент в точке В определяется по зависимости М_B = -R_A·10 + F₁·4 + m;

М_В = -36 ∙10 + 35·4+80 = -140 кН∙м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила R_B. Здесь появляется скачок на величину 71 кН, Q_B = -1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т. к. здесь не приложена внешняя пара сил:

M_D=0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов строим эпюры (эпюры под схемой вала, рис. 30.4)

Задание 1.Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом, построить эпюры попе­речных сил и изгибающих моментов. Найти максимальный изгиба­ющий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавровой балки и прямоугольника с соотношением сто­рон h= 2b. Материал — сталь, допускаемое напряжение 160 МПа. Данные взять из таблицы 8, схема 8.

Таблица 8

Исходные данные	вариант
№ схемы
P, кН
g,кН/м
M, кН · м

Схема 8

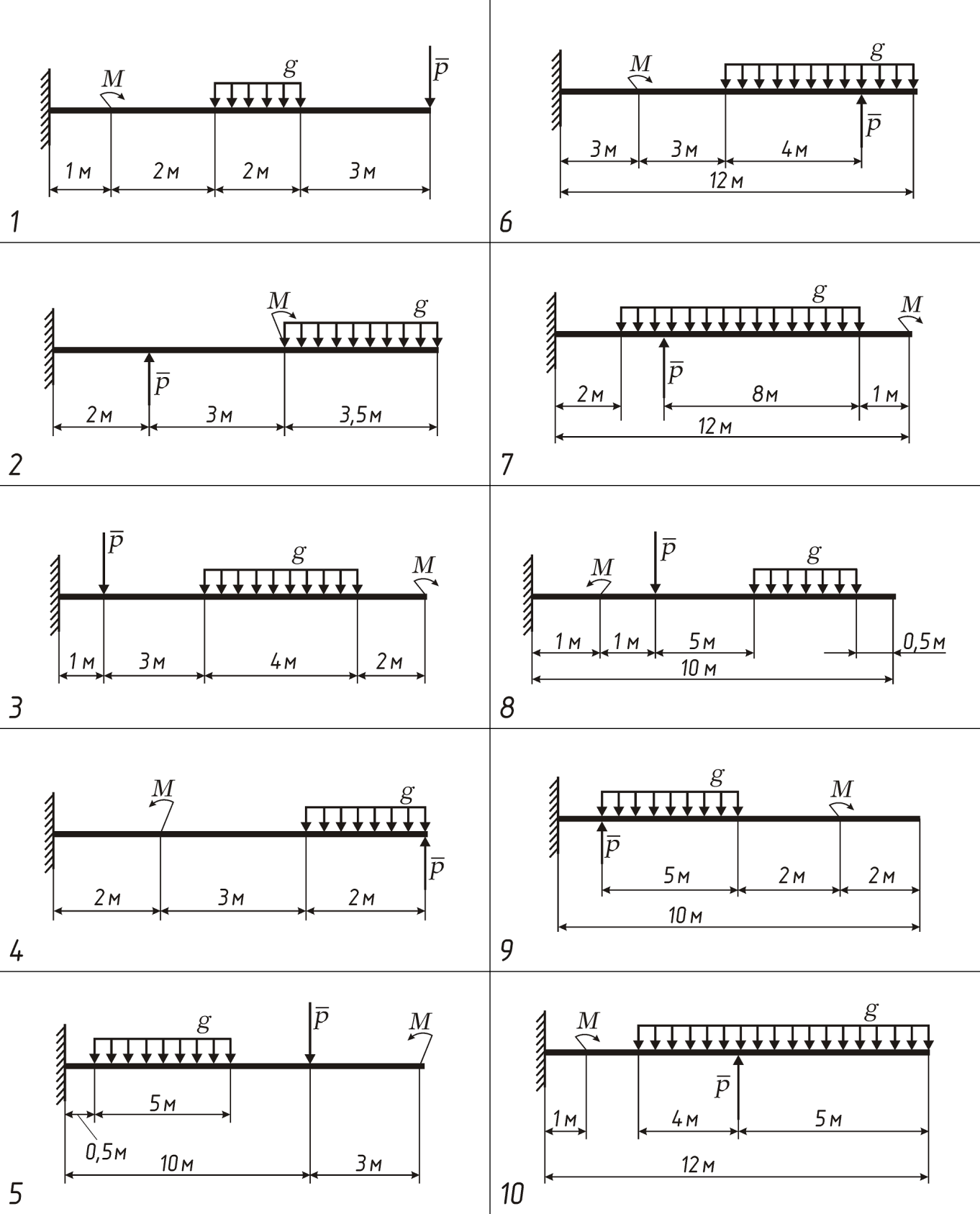
Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПЗ

Разраб.

Провер.

Лит.

Листов

Цель: ________________________________________________________________

Оборудование (приборы, материалы, дидактическое обеспечение)___________________________________________________________

Компьютерная программа (если используется): Наименование программы____________________________________________________________

Дано:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Определить:__________________________________________________________

Решение

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПЗ.

Контрольные вопросы:

1. Напишите формулу для определения нормального напряжения при изгибе

в любой точке поперечного сечения.______________________________________

______________________________________________________________________

2.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

ПЗ.

Напишите формулы для определения момента инерции и момента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин.__________________________________

______________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________

3. Напишите условие прочности при изгибе.____________________________________

______________________________________________________________________________

4. Как принято называть брусья, работающие на прямой изгиб? _______________

____________________________________________________________________

5. Чем характеризуется изгиб? ___________________________________________

____________________________________________________________________

6. В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба? ___________________________________________

____________________________________________________________________

7. Какой изгиб называют плоским?________________________________________

___________________________________________________________________

8. Какой изгиб называется косым? ________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________

9. Какие два внутренних силовых фактора возникают в прямом поперечном изгибе? _______________________________________________________________

__­__________________________________________________________________

10. Чему равен изгибающий момент? Чему равна поперечная сила? ___________________________________________________________________

____________________________________________________________________

Практическое занятие 7

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

ИМПЕРАТОРА АЛЕКСАНДРА I»

(ФГБОУ ВПО ПГУПС)

ПЕТРОЗАВОДСКИЙ ФИЛИАЛ

Практическое занятие 7

Расчеты передач

(Выполнение расчёта прямозубых передач и определение параметров зубчатых колёс)

Практическое занятие 7

Расчеты передач

(Выполнение расчёта прямозубых передач и определение параметров зубчатых колёс)

К выполнению задания необходимо приступить после изучения темы 3.2. «Механические передачи. Детали и сборочные единицы передач»

Цель: ознакомление с конструкцией и назначением зубчатых передач;

- составление кинематической схемы зубчатой передачи;

- научиться выполнять расчет на контактную прочность и изгиб;

- определять основные геометрические параметры.